8.5 垂直 课件 (共25张PPT)2022—2023学年青岛版数学七年级下册
文档属性
| 名称 | 8.5 垂直 课件 (共25张PPT)2022—2023学年青岛版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 363.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 07:34:55 | ||
图片预览






文档简介
(共25张PPT)
垂直
观察思考
当转动一木条的位置时,什么也随着发生了变化?此时,两条直线有什么位置关系
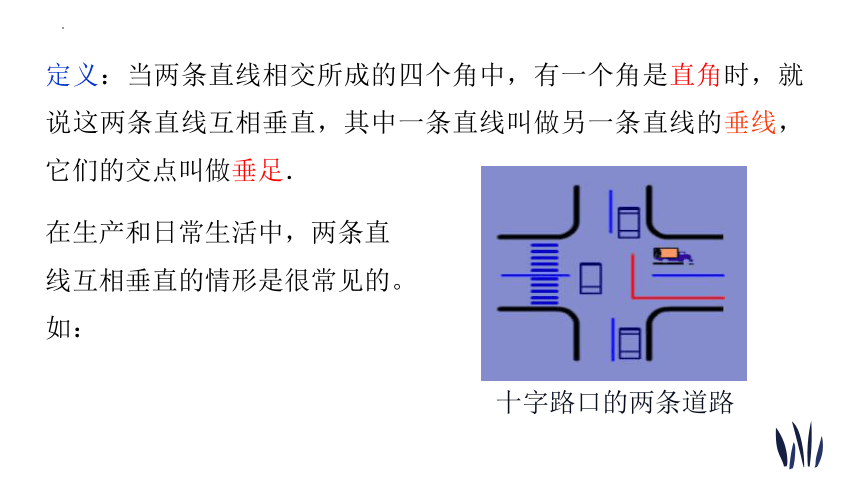
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
在生产和日常生活中,两条直线互相垂直的情形是很常见的。如:
十字路口的两条道路
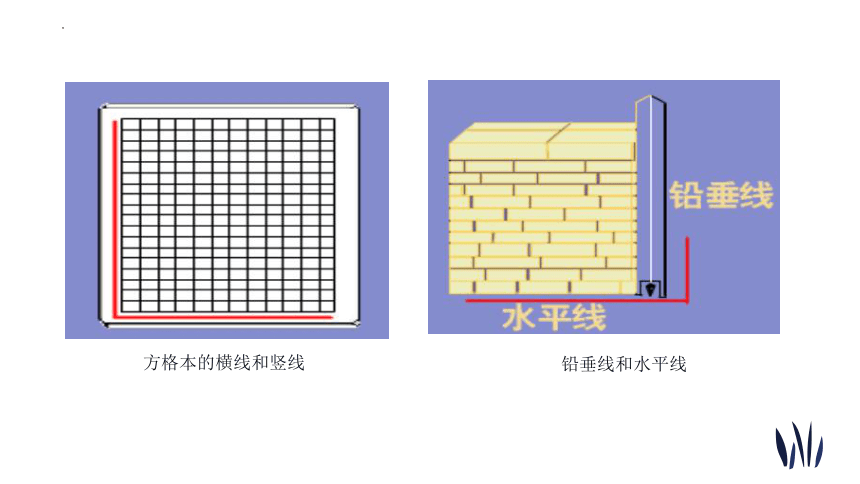
方格本的横线和竖线
铅垂线和水平线
垂直表示方法、读法
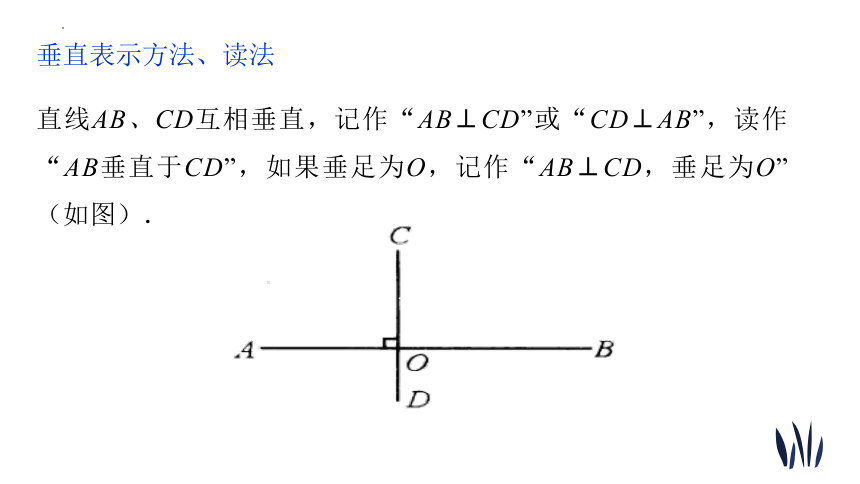
直线AB、CD互相垂直,记作“AB⊥CD”或“CD⊥AB”,读作“AB垂直于CD”,如果垂足为O,记作“AB⊥CD,垂足为O”(如图).
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于o
A
B
O
E
记作: AB⊥OE垂足为O.
或者OE ⊥ AB于O
如何判断两条
直线互相垂直?
由两条直线互相垂直你能得到什么?
用途?
条件和结论
垂直的判定
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义)
如果直线AB、CD 相交于点O,∠AOC=90°,那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义)
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
实例:
体育课上跳远,你应该沿什么方向起跳?
那么我们如何画出垂线呢?
你想到哪些画垂线的方法?
垂线的画法:
(1)过直线上一点画已知直线的垂线
(2)过直线外一点画已知直线的垂线
垂线的画法:
(1)过直线上一点画已知直线的垂线
A
P
B
C
D
3画线:沿着三角板的另一直角边画出垂线.
2移:移动三角板到已知点;
1靠:把三角板的一直角边靠在直线上;
垂线的画法:
(1)过直线外一点画已知直线的垂线
A
P
B
C
D
3画线:沿着三角板的另一直角边画出垂线.
2移:移动三角板到已知点;
1靠:把三角板的一直角边靠在直线上;
垂线的性质
垂线的性质1:过一点有且只有一条直线与已知直线垂直.
问题4:
(1)“过一点”包括几种情况?
(2)“有且只有”是什么意思?
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
1.如图,分别过A、B、C
作BC、AC、AB的垂线。
A
B
C
2.如图,过P分别作OA、OB的垂线。
O
A
B
P
D
E
F
M
N
解:如图、AD⊥BC于D、BE⊥AC于E、CF⊥AB于F
解:如图、PM⊥OA于M、PN⊥OB于N
课堂练习
1.选择题
(1) 过点P向线段AB所在直线引垂线,正确的是( ).
A B C D
C
选择题:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是 ( )
A 有两个角相等 B 有两对角相等
C 有三个角相等 D 有四对邻补角
C
2如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是 。
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
C
D
A
B
O
E
1
2
知识探究
.
P
.
.
.
.
.
.
.
.
.
O
A1
A2
A3
A4
连接直线外一点与直线上各点的所有线段中,垂线段最短
或说成垂线段最短
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
1.如图,要把水渠中的水引到C点,在渠岸AB的什么
地方开沟,才能使沟最短?画出图形,并说明理由.
解:如图,过C作CD⊥AB,垂足为D,
在D处开沟,则沟最短.
因为直线外一点与直线上各点连线的所有线段
中,垂线段最短.
2.如图所示,某村庄计划将河水引到水池C中用于
农田灌溉,怎样挖渠道最短?请说明理由.
解:先作CD⊥AB,垂足为D,然后沿CD开渠,能使
所开的渠道最短.
理由:从直线外一点到这条直线所作的垂线段最短.
3.你能量出图中点P到直线AB的距离吗?
解:过点P在作PD⊥AB于D,则线段PD的长度就是P
到直线AB的距离.
4.如图所示,某自来水厂计划把河流AB中的水引到蓄水池C中,问从河岸AB的何处开渠,才能使所开的渠道最短?画图表示,并说明设计的理由.
解:如图所示.从河岸AB的D点处开渠,可使所开的渠道最短.理由是垂线段最短.
5.如图所示,在正方形ABCD的对角线AC上有一只蚂蚁P从点A出发,沿AC匀速行走,蚂蚁从A点到C点行进过程中:
(1)所经过的点P到AD,BC边的距离是怎么变化的?
(2)所经过点P到CD,BC边距离有何数量关系?为什么呢?
解:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB⊥BC,
∴AD与BC之间的距离等于AB的长,
∵点P在AC上,
∴点P到AD,BC边的距离和等于线段AB的长;
(2)∵四边形ABCD是正方形,AC是对角线,
∴AC是∠BCD的平分线,
∴P到CD,BC边距离相等.
垂直
观察思考
当转动一木条的位置时,什么也随着发生了变化?此时,两条直线有什么位置关系
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
在生产和日常生活中,两条直线互相垂直的情形是很常见的。如:
十字路口的两条道路
方格本的横线和竖线
铅垂线和水平线
垂直表示方法、读法
直线AB、CD互相垂直,记作“AB⊥CD”或“CD⊥AB”,读作“AB垂直于CD”,如果垂足为O,记作“AB⊥CD,垂足为O”(如图).
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于o
A
B
O
E
记作: AB⊥OE垂足为O.
或者OE ⊥ AB于O
如何判断两条
直线互相垂直?
由两条直线互相垂直你能得到什么?
用途?
条件和结论
垂直的判定
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义)
如果直线AB、CD 相交于点O,∠AOC=90°,那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义)
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
实例:
体育课上跳远,你应该沿什么方向起跳?
那么我们如何画出垂线呢?
你想到哪些画垂线的方法?
垂线的画法:
(1)过直线上一点画已知直线的垂线
(2)过直线外一点画已知直线的垂线
垂线的画法:
(1)过直线上一点画已知直线的垂线
A
P
B
C
D
3画线:沿着三角板的另一直角边画出垂线.
2移:移动三角板到已知点;
1靠:把三角板的一直角边靠在直线上;
垂线的画法:
(1)过直线外一点画已知直线的垂线
A
P
B
C
D
3画线:沿着三角板的另一直角边画出垂线.
2移:移动三角板到已知点;
1靠:把三角板的一直角边靠在直线上;
垂线的性质
垂线的性质1:过一点有且只有一条直线与已知直线垂直.
问题4:
(1)“过一点”包括几种情况?
(2)“有且只有”是什么意思?
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
1.如图,分别过A、B、C
作BC、AC、AB的垂线。
A
B
C
2.如图,过P分别作OA、OB的垂线。
O
A
B
P
D
E
F
M
N
解:如图、AD⊥BC于D、BE⊥AC于E、CF⊥AB于F
解:如图、PM⊥OA于M、PN⊥OB于N
课堂练习
1.选择题
(1) 过点P向线段AB所在直线引垂线,正确的是( ).
A B C D
C
选择题:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是 ( )
A 有两个角相等 B 有两对角相等
C 有三个角相等 D 有四对邻补角
C
2如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是 。
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
C
D
A
B
O
E
1
2
知识探究
.
P
.
.
.
.
.
.
.
.
.
O
A1
A2
A3
A4
连接直线外一点与直线上各点的所有线段中,垂线段最短
或说成垂线段最短
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
1.如图,要把水渠中的水引到C点,在渠岸AB的什么
地方开沟,才能使沟最短?画出图形,并说明理由.
解:如图,过C作CD⊥AB,垂足为D,
在D处开沟,则沟最短.
因为直线外一点与直线上各点连线的所有线段
中,垂线段最短.
2.如图所示,某村庄计划将河水引到水池C中用于
农田灌溉,怎样挖渠道最短?请说明理由.
解:先作CD⊥AB,垂足为D,然后沿CD开渠,能使
所开的渠道最短.
理由:从直线外一点到这条直线所作的垂线段最短.
3.你能量出图中点P到直线AB的距离吗?
解:过点P在作PD⊥AB于D,则线段PD的长度就是P
到直线AB的距离.
4.如图所示,某自来水厂计划把河流AB中的水引到蓄水池C中,问从河岸AB的何处开渠,才能使所开的渠道最短?画图表示,并说明设计的理由.
解:如图所示.从河岸AB的D点处开渠,可使所开的渠道最短.理由是垂线段最短.
5.如图所示,在正方形ABCD的对角线AC上有一只蚂蚁P从点A出发,沿AC匀速行走,蚂蚁从A点到C点行进过程中:
(1)所经过的点P到AD,BC边的距离是怎么变化的?
(2)所经过点P到CD,BC边距离有何数量关系?为什么呢?
解:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB⊥BC,
∴AD与BC之间的距离等于AB的长,
∵点P在AC上,
∴点P到AD,BC边的距离和等于线段AB的长;
(2)∵四边形ABCD是正方形,AC是对角线,
∴AC是∠BCD的平分线,
∴P到CD,BC边距离相等.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
