13.4课题学习 最短路径问题 教学设计 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.4课题学习 最短路径问题 教学设计 2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 07:38:14 | ||
图片预览


文档简介
13.4课题学习 最短路径问题
【内容解析】
最短路径问题在现实生活中经常遇到,初中阶段主要以“两点之间,线段最短”“连接直线外一点与直线上各点的所有线段中,垂线段最短”为基础知识,有时还要借助轴对称、平移、旋转等变换进行研究.
本节课以数学史中的两个经典问题——“将军饮马问题”“造桥选址”为载体开展对“最短路径问题”的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称﹑平移等变化将线段和最小问题转化为“两点之间,线段最短”(或“三角形两边之和大于第三边”)问题.
【教学目标】
(1)能利用轴对称﹑平移变化解决简单的最短路径问题,体会图形的变化在解决最值问题中的作用.
(2)在探索最短路径的过程中,感悟﹑应用转化思想.
【教学重、难点】
利用轴对称﹑平移将最短路径问题转化为“两点之间,线段最短”问题.
【教学过程】
一、情境引入
一位将军要从A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路径最短?
[设计意图]利用问题情景,从学生熟悉的生活情景中抛出数学问题,既增强学生的探究欲望,调动学生学习热情.同时也体现了数学与生活的联系.
二、导入新知
1.你能从这个实际问题中抽象出数学模型吗?
师生活动:学生回答——将A,B两地抽象为两个点,将河l抽象为一条直线,如图.
2.你能用自己的语言将这个实际问题抽象为数学问题吗?
师生活动:学生尝试回答,并互相补充,最后达成共识:设C是直线l上的一个动点,当C在l 的什么位置时,AC与CB的和最小.
设计意图:让学生将实际问题抽象为数学问题,即将最短路径问题抽象为“线段和最小问题”.
三、自主探究
问题1 如图,点A,B 在直线l 的同侧,点C 是直线上的一个动点,当点C 在l 的什么位置时,AC 与CB 的和最小?
师生活动:学生独立思考,画图分析,并尝试回答,相互补充.
如果学生有困难,教师可适时提示:
(1)如果点B在点A的异侧,如何在直线l上找到一点C,使AC与BC的和最小?
(2)现在点B与点A在同侧,能否将点B移到l 的另一侧点B′处,且满足直线l上的任意一点C,都能保持CB = C B′吗
(3)此时,点B与点B′有怎样的位置关系?
师生活动:学生叙述,教师板书,并画图,同时学生在自己的练习本上画图.
[设计意图]通过搭建台阶,为学生探究问题提供“脚手架”,将“同侧”难与解决的问题转化为“异侧”容易解决的问题,渗透转化思想.
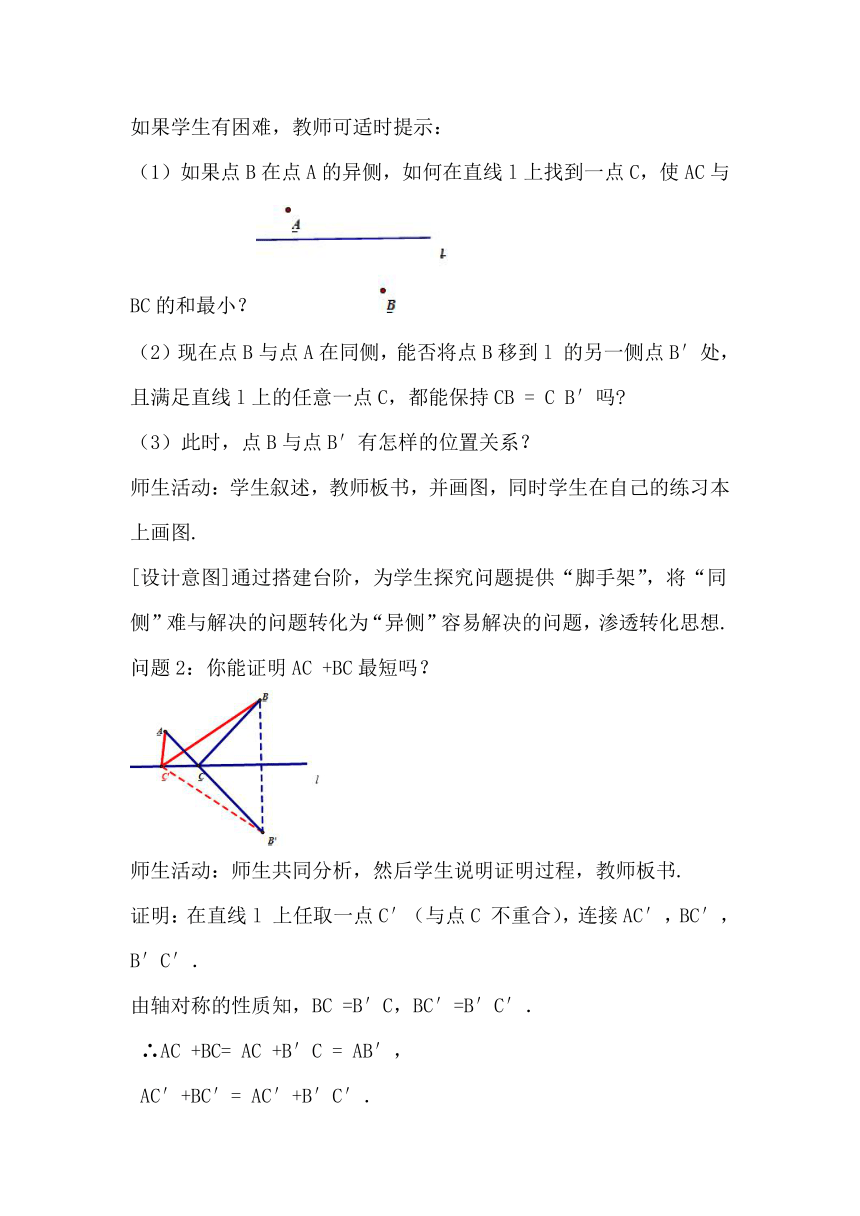
问题2:你能证明AC +BC最短吗?
师生活动:师生共同分析,然后学生说明证明过程,教师板书.
证明:在直线l 上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.
由轴对称的性质知,BC =B′C,BC′=B′C′.
∴AC +BC= AC +B′C = AB′,
AC′+BC′= AC′+B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴AC +BC<AC′+BC′.
即AC +BC最短.
追问1:证明AC +BC最短时,为什么要在直线上任取一点C′(与点C 不重合)呢?
师生活动:学生互相交流,教师适时点拨,最后达成共识:若直线l上任意一点(与点C不重合),与A,B两点的距离和都大于AC+BC,就说明AC+BC最小.
[设计意图]让学生进一步体会作法的正确性,提高逻辑思维能力.
追问2:回顾前面的探究过程,我们是通过怎样的过程,借助什么解决问题的?
师生活动:学生回答,并互相补充.
[设计意图]让学生进一步体会轴对称的“桥梁”作用,感悟转化思想,丰富教学活动经验.
四、类比探究
如图所示,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)
1.抽象出数学图形及数学问题.
如图,a∥b,点A 和点B是两条平行线a与b外的两点,当点N在直线b的什么位置时, AM+MN+NB最小?
2.教师结合几何画板演示让学生观察:
随着点N在直线b上的位置的改变,观察 AM、MN 、NB 的长度,你有什么发现?
3.小组讨论,交流,全班展示解决问题方法:
方法呈现(之一)
将AM沿与河岸垂直的方向平移,点M移到点N,点A移到点A′连接A′B ,线段A′B与直线b的交点N的位置即为所求,
问题:
1.上述最短路径问题,我们借助了哪些图形变化将问题化难为易,运用了什么知识解决的?
2.你能说说解决最短路径问题的基本策略吗?
五、随堂练习
如图,一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客,然后将游客送往河岸BC 上,再返回P 处,请画出旅游船的最短路径.
六、课堂小结
教师与学生一起回顾本节课所学的内容,并请学生回答以下问题:
1.本节课研究的最短路径问题主要用到了什么知识?
2.轴对称与平移在所研究问题中起什么作用?
七、布置作业
课本第91页复习题13的第15题
【内容解析】
最短路径问题在现实生活中经常遇到,初中阶段主要以“两点之间,线段最短”“连接直线外一点与直线上各点的所有线段中,垂线段最短”为基础知识,有时还要借助轴对称、平移、旋转等变换进行研究.
本节课以数学史中的两个经典问题——“将军饮马问题”“造桥选址”为载体开展对“最短路径问题”的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称﹑平移等变化将线段和最小问题转化为“两点之间,线段最短”(或“三角形两边之和大于第三边”)问题.
【教学目标】
(1)能利用轴对称﹑平移变化解决简单的最短路径问题,体会图形的变化在解决最值问题中的作用.
(2)在探索最短路径的过程中,感悟﹑应用转化思想.
【教学重、难点】
利用轴对称﹑平移将最短路径问题转化为“两点之间,线段最短”问题.
【教学过程】
一、情境引入
一位将军要从A 地出发,到一条笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使他所走的路径最短?
[设计意图]利用问题情景,从学生熟悉的生活情景中抛出数学问题,既增强学生的探究欲望,调动学生学习热情.同时也体现了数学与生活的联系.
二、导入新知
1.你能从这个实际问题中抽象出数学模型吗?
师生活动:学生回答——将A,B两地抽象为两个点,将河l抽象为一条直线,如图.
2.你能用自己的语言将这个实际问题抽象为数学问题吗?
师生活动:学生尝试回答,并互相补充,最后达成共识:设C是直线l上的一个动点,当C在l 的什么位置时,AC与CB的和最小.
设计意图:让学生将实际问题抽象为数学问题,即将最短路径问题抽象为“线段和最小问题”.
三、自主探究
问题1 如图,点A,B 在直线l 的同侧,点C 是直线上的一个动点,当点C 在l 的什么位置时,AC 与CB 的和最小?
师生活动:学生独立思考,画图分析,并尝试回答,相互补充.
如果学生有困难,教师可适时提示:
(1)如果点B在点A的异侧,如何在直线l上找到一点C,使AC与BC的和最小?
(2)现在点B与点A在同侧,能否将点B移到l 的另一侧点B′处,且满足直线l上的任意一点C,都能保持CB = C B′吗
(3)此时,点B与点B′有怎样的位置关系?
师生活动:学生叙述,教师板书,并画图,同时学生在自己的练习本上画图.
[设计意图]通过搭建台阶,为学生探究问题提供“脚手架”,将“同侧”难与解决的问题转化为“异侧”容易解决的问题,渗透转化思想.
问题2:你能证明AC +BC最短吗?
师生活动:师生共同分析,然后学生说明证明过程,教师板书.
证明:在直线l 上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.
由轴对称的性质知,BC =B′C,BC′=B′C′.
∴AC +BC= AC +B′C = AB′,
AC′+BC′= AC′+B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴AC +BC<AC′+BC′.
即AC +BC最短.
追问1:证明AC +BC最短时,为什么要在直线上任取一点C′(与点C 不重合)呢?
师生活动:学生互相交流,教师适时点拨,最后达成共识:若直线l上任意一点(与点C不重合),与A,B两点的距离和都大于AC+BC,就说明AC+BC最小.
[设计意图]让学生进一步体会作法的正确性,提高逻辑思维能力.
追问2:回顾前面的探究过程,我们是通过怎样的过程,借助什么解决问题的?
师生活动:学生回答,并互相补充.
[设计意图]让学生进一步体会轴对称的“桥梁”作用,感悟转化思想,丰富教学活动经验.
四、类比探究
如图所示,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)
1.抽象出数学图形及数学问题.
如图,a∥b,点A 和点B是两条平行线a与b外的两点,当点N在直线b的什么位置时, AM+MN+NB最小?
2.教师结合几何画板演示让学生观察:
随着点N在直线b上的位置的改变,观察 AM、MN 、NB 的长度,你有什么发现?
3.小组讨论,交流,全班展示解决问题方法:
方法呈现(之一)
将AM沿与河岸垂直的方向平移,点M移到点N,点A移到点A′连接A′B ,线段A′B与直线b的交点N的位置即为所求,
问题:
1.上述最短路径问题,我们借助了哪些图形变化将问题化难为易,运用了什么知识解决的?
2.你能说说解决最短路径问题的基本策略吗?
五、随堂练习
如图,一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客,然后将游客送往河岸BC 上,再返回P 处,请画出旅游船的最短路径.
六、课堂小结
教师与学生一起回顾本节课所学的内容,并请学生回答以下问题:
1.本节课研究的最短路径问题主要用到了什么知识?
2.轴对称与平移在所研究问题中起什么作用?
七、布置作业
课本第91页复习题13的第15题
