2015连线中考数学一轮复习系列专题15三角形与解直角三角形
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题15三角形与解直角三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 18:39:55 | ||
图片预览




文档简介
第十五讲 三角形与直角三角形
基础知识
知识点一:三角形的有关概念及性质
三角形的定义:由不在同一直线的三条线段首 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )尾顺次连接所组成的封闭图形叫做三角形。其中这三条线段叫做三角形的三条边,三条线段两两构成的角叫做三角形的内角。
三角形的分类
①、按三角形的三边的关系分类
②、按三角形的三个角的关系分类
把边和角联系在一起,我们又得到一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
注意:三角形具有稳定性
在同一个三角形中,等边对等角;等角对等边;大角对大边;小角对小边。
三角形的有关线和角
①、线
、边:组成三角形的三条线段叫做三角形的三条边,其线段的长度成为三角形的边长。
、高:是过三角形的一个顶点向这个顶点的对边作的一条垂线。
、中线:是三角形的一个顶点与这个顶点所对应的边的中点的连线。
、角平分线:从三角形的一个角的顶点引出一条线,把这个角分成两个完全相同的角,这条线叫做三角形这个角的角平分线
( http: / / www.21cnjy.com )
三角形的内角和定理及推论
三角形的内角和定理:三角形三个内角和等于180°;
推论:
①、直角三角形的两个锐角互余;
②、三角形的一个外角等于和它不相邻的来两个内角的和;
③、三角形的一个外角大于任何一个和它不相邻的内角。
三角形的三边关系定理及推论
三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
注:在利用三角形的三边关系时应注意满足“三 ( http: / / www.21cnjy.com )角形的两边之差小于第三边”不一定满足“三角形的两边之和大于第三边”;满足“三角形的两边之和大于第三边”一定满足“三角形的两边之差小于第三边”。
知识点二、解直角三角形
勾股定理
勾股定理的概念:直角三角形斜边的平方等于两直角边的平方和。
数学表达:若为直角三角形,,,的对边分别为,,,且,则。
勾股定理的逆定理:若中,,的对边分别为,,,且,则是的直角三角形。
锐角三角函数
①、锐角三角函数定义:
在中,,设,,,锐角的四个三角函数是:
(1)、正弦定义:在中,锐角的对边与斜边的比叫做角的正弦,记作,即;
(2)、余弦定义:在中,锐角的邻边与斜边的比叫做角的正弦,记作,即;
(3)、正切定义:在中,锐角的对边与邻边的比叫做角的正切,记作,即;
( http: / / www.21cnjy.com )
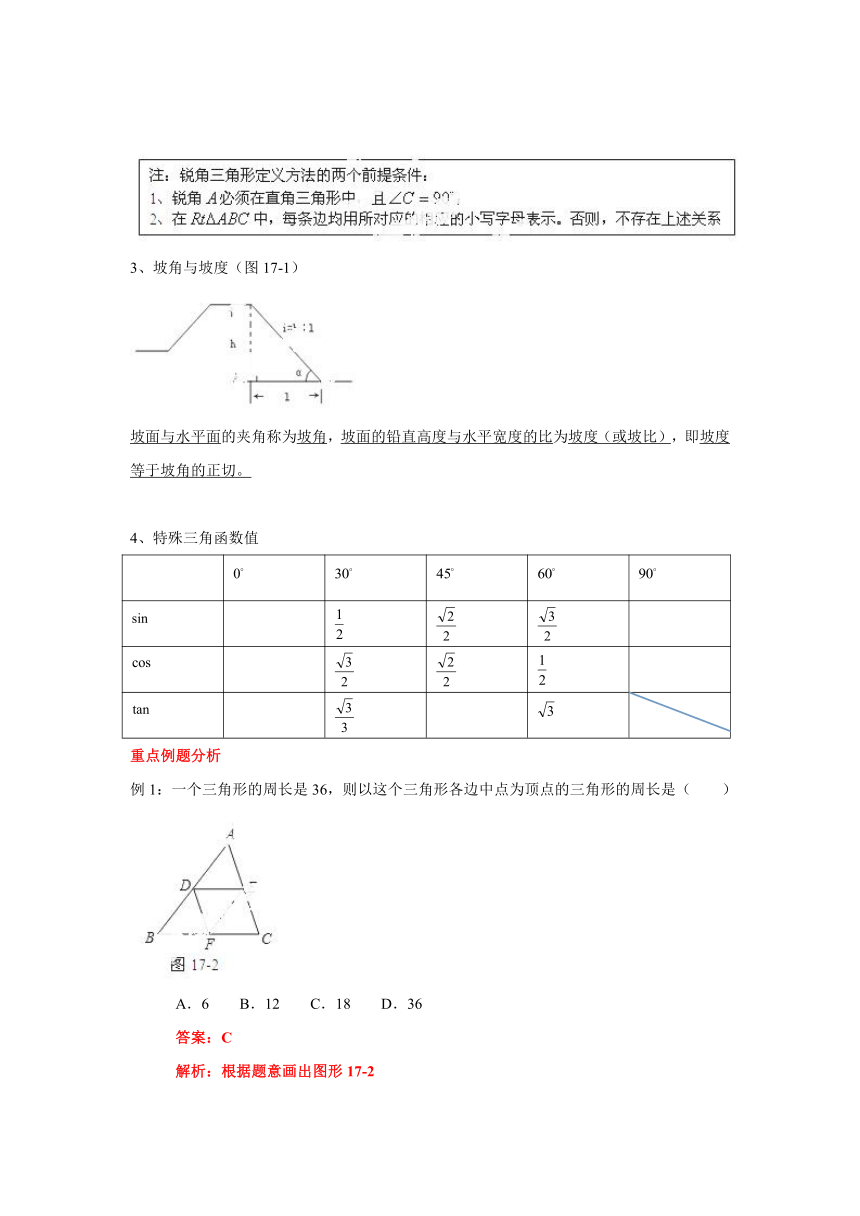
坡角与坡度(图17-1)
( http: / / www.21cnjy.com )
坡面与水平面的夹角称为坡角,坡面的铅直高度与水平宽度的比为坡度(或坡比),即坡度等于坡角的正切。
特殊三角函数值
重点例题分析
例1:一个三角形的周长是36,则以这个三角形各边中点为顶点的三角形的周长是( ) ( http: / / www.21cnjy.com )
A.6 B.12 C.18 D.36
答案:C
解析:根据题意画出图形17-2
因为D、E、F分别是AF、AC、BC的中点
所以由三角形的中位线定理可知DE=0.5BC,DF=0.5AC,EF=0.5AB
∵AB+CB+AC=36,∴DE+DF+FE=36÷2=18。故选C。
例2:等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A. 12 B. 15 C. 12或15 D. 18
( http: / / www.21cnjy.com )
例3:如图17-3,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
( http: / / www.21cnjy.com )
A.18° B.24° C.30° D.36°
( http: / / www.21cnjy.com )
例4:如图17-4,在Rt△ABC中,∠A ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 15
.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )例5:如图17-5,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于( )
A. B.
C. D.
答案:C
解析:如图,过P作PE⊥x轴于E,
∵P(12,5),
∴PE=5,OE=12,
∴tanα==,
故选C.
例6:在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA= ;②cosB=;③tanA=;④tanB= ,其中正确的结论是 ②③④
(只需填上正确结论的序号)
答案:②③④
解:如图所示:
( http: / / www.21cnjy.com )
例7:在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= 6
.
( http: / / www.21cnjy.com )
例8:如图17-6,已知∠AOB=60° ( http: / / www.21cnjy.com ),点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A. 3 B. 4 C. 5 D. 6
( http: / / www.21cnjy.com )
例9:在平面直角坐标系中,O为坐标原点,点A的坐标为(1,),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为( )
A. 4 B. 5 C. 6 D. 8
( http: / / www.21cnjy.com )
例10:如图17-6,Rt ( http: / / www.21cnjy.com )△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
( http: / / www.21cnjy.com )
A.: B. C. 4 D. 5
( http: / / www.21cnjy.com )
巩固练习
若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长为( )
A.5 B.7 C.5或7 D.6
2.如图17-7,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
A.68° B.32° C.22° D.16°
( http: / / www.21cnjy.com )
3.如图17-8,从热气球C处测得地面 ( http: / / www.21cnjy.com )A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B. 米 C. 米 D. 米
( http: / / www.21cnjy.com )
4.如图17-9,轮船从B处以每小 ( http: / / www.21cnjy.com )时海里的速度沿男偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是( )海里
( http: / / www.21cnjy.com )
A. B. C. 50 D.25
5.如图①是一个直角三角形纸片,∠ ( http: / / www.21cnjy.com )A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,则折痕DE的长为( )
A. cm B. 2cm C. 2cm D. 3cm
( http: / / www.21cnjy.com )
6.如图17-10,在Rt△ABC中,∠C= ( http: / / www.21cnjy.com )90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是 .
( http: / / www.21cnjy.com )
7.如图17-11,Rt△ ( http: / / www.21cnjy.com )ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为 .
( http: / / www.21cnjy.com )
8.如图17-12,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(≈1.414,精确到1米)
( http: / / www.21cnjy.com )
9.如图17-13,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长,
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
中考预测
1.河堤横断面如图17-14所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为( )
A.12 B.4米 C.5米 D.6米
( http: / / www.21cnjy.com )
如图17-15,在Rt△ABC中,∠ACB ( http: / / www.21cnjy.com )=60°,DE是斜边AC的中垂线,分别交AB、AC于D、E两点.若BD=2,则AC的长是( )
A.4 B. C.8 D.
( http: / / www.21cnjy.com )
3.如图17-16,在△ ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.4cm B.3cm C.2cm D.1cm
( http: / / www.21cnjy.com )
4.在一次数学活动中,李明利用一根拴有 ( http: / / www.21cnjy.com )小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图17-17,已知李明距假山的水平距离BD为12m,他的眼睛距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )
( http: / / www.21cnjy.com )
A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m
5.如图17-18,在四边形ABCD中 ( http: / / www.21cnjy.com ),AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A. B. C. D.
( http: / / www.21cnjy.com )
6.cos30°的值是 .
7.如图17-19,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= 35
°.
( http: / / www.21cnjy.com )
8.如图17-20,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD= 44°
.
( http: / / www.21cnjy.com )
9.如图17-21,有两棵树,一棵 ( http: / / www.21cnjy.com )高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行 米.
( http: / / www.21cnjy.com )
10.如图17-22,有一直角三角形纸片 ( http: / / www.21cnjy.com )ABC,边BC=6,AB=10,∠ACB=90°,将该直角三角形纸片沿DE折叠,使点A与点C重合,则四边形DBCE的周长为 .
( http: / / www.21cnjy.com )
11.如图17-23,已知 ( http: / / www.21cnjy.com )△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 15
度.
( http: / / www.21cnjy.com )
12.已知:如图17-24,在Rt△ ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形。若AB=2,求△ABC的周长。(结果保留根号)
( http: / / www.21cnjy.com )
13.某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).
( http: / / www.21cnjy.com )
答案:
巩固练习
B
( http: / / www.21cnjy.com )
B
( http: / / www.21cnjy.com )
D
( http: / / www.21cnjy.com )
D
( http: / / www.21cnjy.com )
5、A
( http: / / www.21cnjy.com )
6.2
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
中考预测
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
9.10
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图17-12
图17-17
基础知识
知识点一:三角形的有关概念及性质
三角形的定义:由不在同一直线的三条线段首 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )尾顺次连接所组成的封闭图形叫做三角形。其中这三条线段叫做三角形的三条边,三条线段两两构成的角叫做三角形的内角。
三角形的分类
①、按三角形的三边的关系分类
②、按三角形的三个角的关系分类
把边和角联系在一起,我们又得到一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
注意:三角形具有稳定性
在同一个三角形中,等边对等角;等角对等边;大角对大边;小角对小边。
三角形的有关线和角
①、线
、边:组成三角形的三条线段叫做三角形的三条边,其线段的长度成为三角形的边长。
、高:是过三角形的一个顶点向这个顶点的对边作的一条垂线。
、中线:是三角形的一个顶点与这个顶点所对应的边的中点的连线。
、角平分线:从三角形的一个角的顶点引出一条线,把这个角分成两个完全相同的角,这条线叫做三角形这个角的角平分线
( http: / / www.21cnjy.com )
三角形的内角和定理及推论
三角形的内角和定理:三角形三个内角和等于180°;
推论:
①、直角三角形的两个锐角互余;
②、三角形的一个外角等于和它不相邻的来两个内角的和;
③、三角形的一个外角大于任何一个和它不相邻的内角。
三角形的三边关系定理及推论
三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
注:在利用三角形的三边关系时应注意满足“三 ( http: / / www.21cnjy.com )角形的两边之差小于第三边”不一定满足“三角形的两边之和大于第三边”;满足“三角形的两边之和大于第三边”一定满足“三角形的两边之差小于第三边”。
知识点二、解直角三角形
勾股定理
勾股定理的概念:直角三角形斜边的平方等于两直角边的平方和。
数学表达:若为直角三角形,,,的对边分别为,,,且,则。
勾股定理的逆定理:若中,,的对边分别为,,,且,则是的直角三角形。
锐角三角函数
①、锐角三角函数定义:
在中,,设,,,锐角的四个三角函数是:
(1)、正弦定义:在中,锐角的对边与斜边的比叫做角的正弦,记作,即;
(2)、余弦定义:在中,锐角的邻边与斜边的比叫做角的正弦,记作,即;
(3)、正切定义:在中,锐角的对边与邻边的比叫做角的正切,记作,即;
( http: / / www.21cnjy.com )
坡角与坡度(图17-1)
( http: / / www.21cnjy.com )
坡面与水平面的夹角称为坡角,坡面的铅直高度与水平宽度的比为坡度(或坡比),即坡度等于坡角的正切。
特殊三角函数值
重点例题分析
例1:一个三角形的周长是36,则以这个三角形各边中点为顶点的三角形的周长是( ) ( http: / / www.21cnjy.com )
A.6 B.12 C.18 D.36
答案:C
解析:根据题意画出图形17-2
因为D、E、F分别是AF、AC、BC的中点
所以由三角形的中位线定理可知DE=0.5BC,DF=0.5AC,EF=0.5AB
∵AB+CB+AC=36,∴DE+DF+FE=36÷2=18。故选C。
例2:等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A. 12 B. 15 C. 12或15 D. 18
( http: / / www.21cnjy.com )
例3:如图17-3,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
( http: / / www.21cnjy.com )
A.18° B.24° C.30° D.36°
( http: / / www.21cnjy.com )
例4:如图17-4,在Rt△ABC中,∠A ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 15
.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )例5:如图17-5,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于( )
A. B.
C. D.
答案:C
解析:如图,过P作PE⊥x轴于E,
∵P(12,5),
∴PE=5,OE=12,
∴tanα==,
故选C.
例6:在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA= ;②cosB=;③tanA=;④tanB= ,其中正确的结论是 ②③④
(只需填上正确结论的序号)
答案:②③④
解:如图所示:
( http: / / www.21cnjy.com )
例7:在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= 6
.
( http: / / www.21cnjy.com )
例8:如图17-6,已知∠AOB=60° ( http: / / www.21cnjy.com ),点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A. 3 B. 4 C. 5 D. 6
( http: / / www.21cnjy.com )
例9:在平面直角坐标系中,O为坐标原点,点A的坐标为(1,),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为( )
A. 4 B. 5 C. 6 D. 8
( http: / / www.21cnjy.com )
例10:如图17-6,Rt ( http: / / www.21cnjy.com )△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
( http: / / www.21cnjy.com )
A.: B. C. 4 D. 5
( http: / / www.21cnjy.com )
巩固练习
若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长为( )
A.5 B.7 C.5或7 D.6
2.如图17-7,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
A.68° B.32° C.22° D.16°
( http: / / www.21cnjy.com )
3.如图17-8,从热气球C处测得地面 ( http: / / www.21cnjy.com )A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B. 米 C. 米 D. 米
( http: / / www.21cnjy.com )
4.如图17-9,轮船从B处以每小 ( http: / / www.21cnjy.com )时海里的速度沿男偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是( )海里
( http: / / www.21cnjy.com )
A. B. C. 50 D.25
5.如图①是一个直角三角形纸片,∠ ( http: / / www.21cnjy.com )A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,则折痕DE的长为( )
A. cm B. 2cm C. 2cm D. 3cm
( http: / / www.21cnjy.com )
6.如图17-10,在Rt△ABC中,∠C= ( http: / / www.21cnjy.com )90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是 .
( http: / / www.21cnjy.com )
7.如图17-11,Rt△ ( http: / / www.21cnjy.com )ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为 .
( http: / / www.21cnjy.com )
8.如图17-12,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(≈1.414,精确到1米)
( http: / / www.21cnjy.com )
9.如图17-13,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长,
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
中考预测
1.河堤横断面如图17-14所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为( )
A.12 B.4米 C.5米 D.6米
( http: / / www.21cnjy.com )
如图17-15,在Rt△ABC中,∠ACB ( http: / / www.21cnjy.com )=60°,DE是斜边AC的中垂线,分别交AB、AC于D、E两点.若BD=2,则AC的长是( )
A.4 B. C.8 D.
( http: / / www.21cnjy.com )
3.如图17-16,在△ ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.4cm B.3cm C.2cm D.1cm
( http: / / www.21cnjy.com )
4.在一次数学活动中,李明利用一根拴有 ( http: / / www.21cnjy.com )小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图17-17,已知李明距假山的水平距离BD为12m,他的眼睛距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )
( http: / / www.21cnjy.com )
A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m
5.如图17-18,在四边形ABCD中 ( http: / / www.21cnjy.com ),AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A. B. C. D.
( http: / / www.21cnjy.com )
6.cos30°的值是 .
7.如图17-19,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= 35
°.
( http: / / www.21cnjy.com )
8.如图17-20,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD= 44°
.
( http: / / www.21cnjy.com )
9.如图17-21,有两棵树,一棵 ( http: / / www.21cnjy.com )高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行 米.
( http: / / www.21cnjy.com )
10.如图17-22,有一直角三角形纸片 ( http: / / www.21cnjy.com )ABC,边BC=6,AB=10,∠ACB=90°,将该直角三角形纸片沿DE折叠,使点A与点C重合,则四边形DBCE的周长为 .
( http: / / www.21cnjy.com )
11.如图17-23,已知 ( http: / / www.21cnjy.com )△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 15
度.
( http: / / www.21cnjy.com )
12.已知:如图17-24,在Rt△ ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形。若AB=2,求△ABC的周长。(结果保留根号)
( http: / / www.21cnjy.com )
13.某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).
( http: / / www.21cnjy.com )
答案:
巩固练习
B
( http: / / www.21cnjy.com )
B
( http: / / www.21cnjy.com )
D
( http: / / www.21cnjy.com )
D
( http: / / www.21cnjy.com )
5、A
( http: / / www.21cnjy.com )
6.2
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
中考预测
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
9.10
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图17-12
图17-17
同课章节目录
