山东省济南市槐荫区2015届九年级上学期期中考试数学试题(附答案)
文档属性
| 名称 | 山东省济南市槐荫区2015届九年级上学期期中考试数学试题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 326.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 18:36:26 | ||
图片预览



文档简介
济南市槐荫区2015届九年级上学期期中考
数学试题(2014年11月)
本巻共120分,答题时间120分钟。
本试题分第Ⅰ卷(选择题)和第Ⅱ卷 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )(非选择题)两部分.第Ⅰ卷共2页,满分为45分;第Ⅱ卷共6页,满分为75分.本试题共8页,满分为120分.考试时间为120分钟.答卷前,请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷规定的位置.考试结束后,将本试卷和答题卡一并交回.本考试不允许使用计算器.
第I卷(选择题 共45分)
注意事项:
第Ⅰ卷为选择题,每小题选出答案后,用2B铅 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案写在试卷上无效.
一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知4x=5y,则y∶x的值为( )
A.1∶5 B.5:1 C.4:5 D.5:4
2、 在Rt△ABC中,∠C=90°,若AC=2,BC =1,则tanA的值是( )
A. B. C. 2 D.
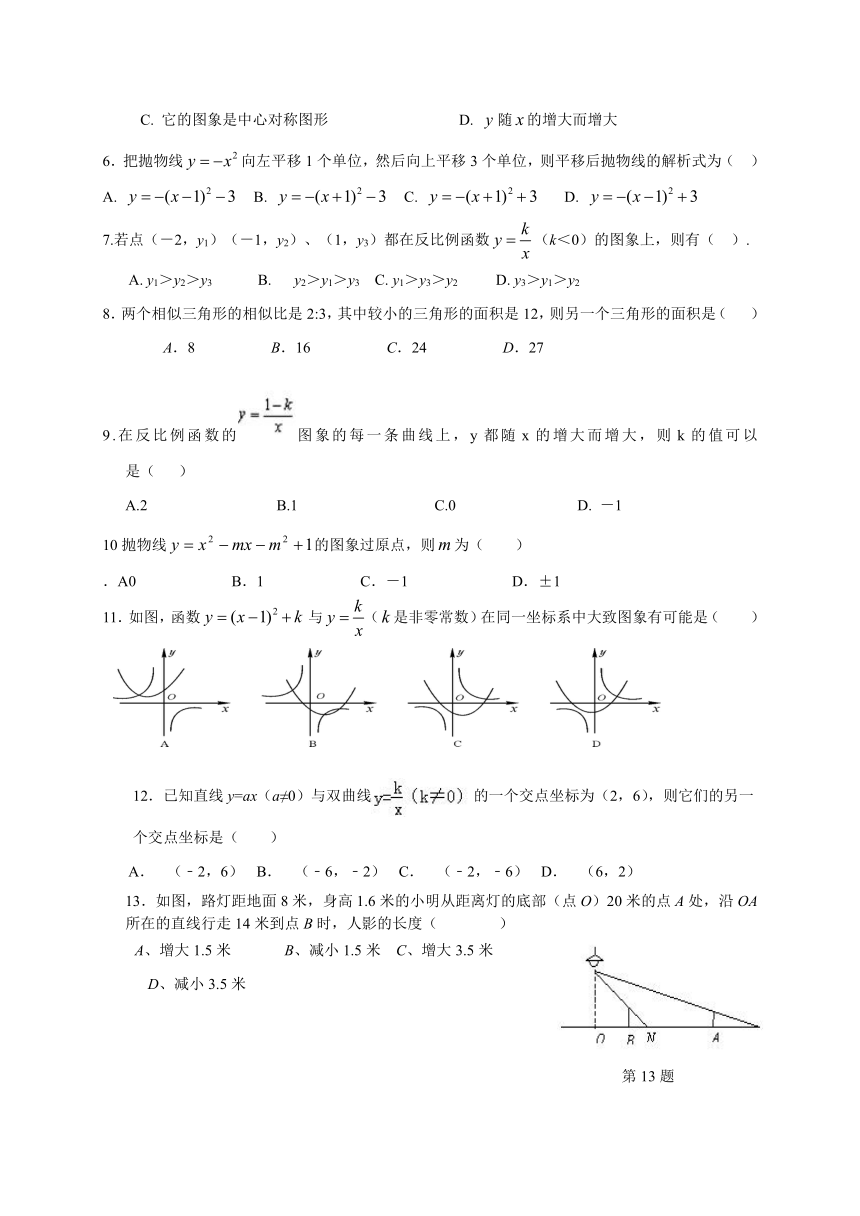
3.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是)
A. 1 B. 1.5 C. 2 D. 3
4.如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA, OB
的中点M,N,测得MN=32 m,则A,B两点间的距离是( )
A.64 m B.16 m C.32 m D.24 m
( http: / / www.21cnjy.com )3题图 4题图 ( http: / / www.21cnjy.com )
5.对于反比例函数,下列说法不正确的是( )
A. 它的图象是双曲线并且在第一、三象限 B. 点(-4,)在它的图象上
C. 它的图象是中心对称图形 D. 随的增大而增大
6.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A. B. C. D.
7.若点(-2,y1)(-1,y2)、(1,y3)都在反比例函数(k<0)的图象上,则有( ).
A. y1>y2>y3 B. y2>y1>y3 C. y1>y3>y2 D. y3>y1>y2
8.两个相似三角形的相似比是2:3,其中较小的三角形的面积是12,则另一个三角形的面积是( )
A.8 B.16 C.24 D.27
9.在反比例函数的图象的每一条曲线上,y都随x的增大而增大,则k的值可以
是( )
A.2 B.1 C.0 D. -1
10抛物线的图象过原点,则为( )
.A0 B.1 C.-1 D.±1
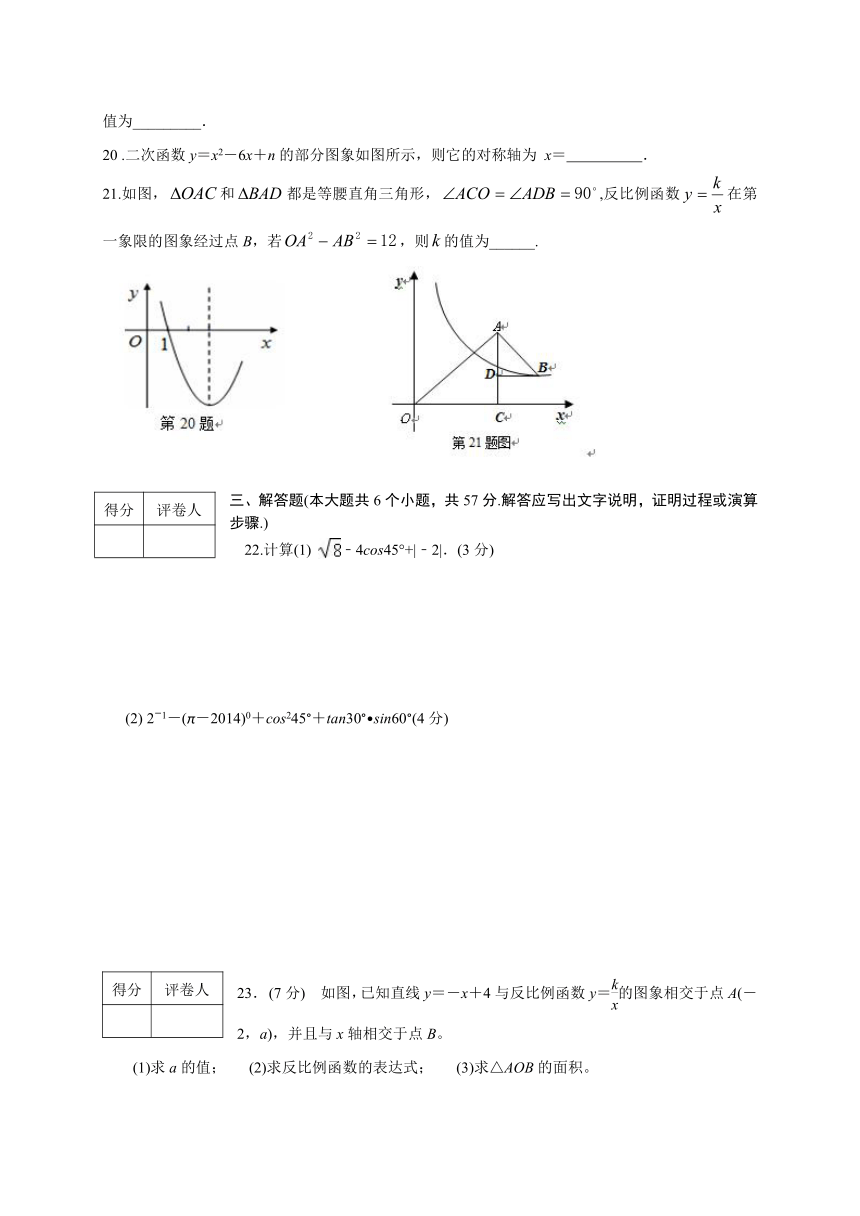
11.如图,函数与(是非零常数)在同一坐标系中大致图象有可能是( )
12.已知直线y=ax(a≠0)与双曲线的一个交点坐标为(2,6),则它们的另一个交点坐标是( )
A. (﹣2,6) B. (﹣6,﹣2) C. (﹣2,﹣6) D. (6,2)
13.如图,路灯距地面8米,身高1.6米的 ( http: / / www.21cnjy.com )小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A、增大1.5米 B、减小1.5米 C、增大3.5米 D、减小3.5米
14.如图所示,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数y=k/x (x>0)的图象与△ABC有公共点,则k的取值范围是( ) ( http: / / www.21cnjy.com )14题图
A.2≤k≤9 B.2≤k≤8 C.2≤k≤5 D.5≤k≤8
15.如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①;②点F是GE的中点;③AF=AB;④S△ABC =5 S△BDF,其确的结论是________ ____.
A .①④ B.① ②③ C. ①③ D. ①②③④
第Ⅱ卷(非选择题 共75分)
注意事项:
1.第Ⅱ卷为非选择题,请考生用蓝、黑色钢笔(签字笔)或圆珠笔直接在试卷上作答.
2.答卷前,请考生先将考点、姓名、准考证号、座号填写在试卷规定的位置.
二、填空题(本大题共6个小题.每小题3分,共18分.把答案填在题中横线上.)
16.某数学兴趣小组测得小强的影长是1m, ( http: / / www.21cnjy.com )同一时刻旗杆的影长是15m.已知小强的身高为1.8m,则旗杆的高度为_________m..
17.在Rt△ABC中,∠C=90°,a=4,b=3,则sinA的值是 _________ ,
18.如图,E是 ABCD的边CD上一点,连接AE并延长交BC的延长线于点F,且AD=4,=,则CF的长为 ________ .
19.设函数与的图象的交点坐标为(a,b),则 的值为_________.
20 .二次函数y=x2-6x+n的部分图象如图所示,则它的对称轴为 x= .
21.如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点B,若,则的值为______.
( http: / / www.21cnjy.com )
得分 评卷人
三、解答题(本大题共6个小题,共57分.解答应写出文字说明,证明过程或演算步骤.)
22.计算(1) ﹣4cos45°+|﹣2|.(3分)
(2) 2-1-(π-2014)0+cos245°+tan30° sin60°(4分)
得分 评卷人
23. (7分) 如图,已知直线y=-x+4与反比例函数y=的图象相交于点A(-2,a),并且与x轴相交于点B。
(1)求a的值; (2)求反比例函数的表达式; (3)求△AOB的面积。
得分 评卷人
24.(8分)如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF
( http: / / www.21cnjy.com )
得分 评卷人
25.(8分)某数学活动小 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在B点测得C点的仰角为30°.已知山顶C点处的高度是600米.(1)求斜坡B点处的高度;(2)求斜坡AB的坡度.
( http: / / www.21cnjy.com )25题图
得分 评卷人
26.(9分)如图,在平面直角坐标系内 ( http: / / www.21cnjy.com ),已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
得分 评卷人
27.(9分) 如图,在直角梯形OABC中,BC//AO,∠AOC=900,点A、B的坐标分别为(5,0)、(2,6),点D为AB上一点,且BD=2AD.双曲线y=(x>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积。
28.(9分)在一个边长为a(单位:cm)的正方形ABCD中.
(1)如图1,如果N是AD中点,F为AB中点,连接DF,CN.
①求证:DF=CN;
②连接AC.则DH:HE: EF=_____________(直接写出结果)
(2)如图2,如果点E、M分别是线段AC、CD上的动点,假设点E从点A出发,以cm/s速度沿AC向点C运动,同时点M从点C出发,以1cm/s的速度沿CD向点D运动,运动时间为t(t>0),连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.。求证:当点F是边AB中点时,DM=2CM
九年级数学试题参考答案与评分标准(2014.11)
一、选择题 CACAD CBDAD BCDAC
二、填空
16. 27 17 4/5 18. 2 19. -1/2
20. 3 21. 6
三、解答题
22.(1)原式=2﹣4×+2=2.………………………3分
(2)原式=-1+( EQ \f(,2))2+ EQ \f(,3) EQ \f(,2)
=-1++
=…………………………4分
23解:(1)将A(-2,a)代入y=-x+4中,得:a=-(-2)+4,所以a=6----------- -2分
(2)由(1)得:A(-2,6)
将A(-2,6)代入y=中,得到:6=,即k=-12
所以反比例函数的表达式为:y=- ----------- 4分
(3)如图:过A点作AD⊥x轴于D;
∵A(-2,6),∴AD=6
在直线y=-x+4中,令y=0,得x=4
∴B(4,0),即OB=4
∴△AOB的面积S=OB×AD=×4×6=12.………….7分
24. 解:∵AB∥ CD
∴△ABE∽△CDE
∴AB:CD=BE:ED
∵AB=6cm,CD=12cm
∴AB:CD=1:2=BE:CD
∴BE:BD=1:3………………………..4分
∵EF∥CD
∴△BEF∽△BDC
∴EF:CD=BE:BD=1:3
∵CD=12cm ∴ EF=4cm………………8分
25 解:(1)如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足.(1分)
在B点测得C点的仰角为30°,
∴∠CBD=30°,又BC=400米,
∴CD=400×sin30°=400×=200(米).----------- 3分
∴B点的铅直高度为600﹣200=400(米).----------- 4分
(2)∵BE=400米,
∴AB=1040米,AE===960米,----------- -6分
∴AB的坡度iAB===,----------- -8分
26 解:(1)设直线AB的解析式为y=kx+b
由题意,得 解得
所以,直线AB的解析式为y=-x+6.………………………….4 分
(2)由AO=6, BO=8 得AB=10
所以AP=t ,AQ=10-2t
分两种情况:
1° 当∠APQ=∠AOB时,△APQ∽△AOB.
所以 = 解得 t=(秒) …………….6分
2° 当∠AQP=∠AOB时,△AQP∽△AOB.
所以 = 解得 t=(秒) ………………8分
∴t=秒或秒时,△APQ与△AOB相似…………………………….9分
27(1)①易证△ADF≌△DCN,则DF=CN;3分
②6:4:5 ……………………………………………………………5分
(2)过点E作EG⊥AD于点G,
依题意得,AE=,易求AG=EG=t,…………6分
CM=t,DG=DM=
易证△DGE≌△MDN,∴……….7分
由△ADF∽△DMN,得,
又∵点F是线段AB中点,AB=AD,
∴,
∴DM=2DN
∵DN=CM
∴DM=2CM………………………………………………………………………9分
28解:(1)过点B、D作x轴的的垂线,垂足分别为点M、N.
∵A (5.0)、B(2,6),∴OM=BC=2,BM=OC=6,AM=3.
∵DN∥BM,∴△AND∽△ABM.
∴
∴DN =2,AN=1, ∴ON=4
∴点D的坐标为(4,2).…………………………3分
又∵ 双曲线y=(x>0)经过点D,
∴k=2×4=8
∴双曲线的解析式为y=.………………………5分
(2)∵点E在BC上,∴点E的纵坐标为6.
又∵点E在双曲线y=上,
∴点E的坐标为(,6),∴CE=………………………7分
∴S四边形ODBE=S梯形OABC-S△OCE-S△AOD
=×(BC+OA)×OC-×OC×CE-×OA×DN
=×(2+5)×6-×6×-×5×2
=12
∴四边形ODBE的面积为12. ………………………………9分
装 订 线
班级 姓名 考场 考号 序号
第13题
第15题
x
O
P
y
A
Q
B
数学试题(2014年11月)
本巻共120分,答题时间120分钟。
本试题分第Ⅰ卷(选择题)和第Ⅱ卷 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )(非选择题)两部分.第Ⅰ卷共2页,满分为45分;第Ⅱ卷共6页,满分为75分.本试题共8页,满分为120分.考试时间为120分钟.答卷前,请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷规定的位置.考试结束后,将本试卷和答题卡一并交回.本考试不允许使用计算器.
第I卷(选择题 共45分)
注意事项:
第Ⅰ卷为选择题,每小题选出答案后,用2B铅 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案写在试卷上无效.
一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知4x=5y,则y∶x的值为( )
A.1∶5 B.5:1 C.4:5 D.5:4
2、 在Rt△ABC中,∠C=90°,若AC=2,BC =1,则tanA的值是( )
A. B. C. 2 D.
3.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是)
A. 1 B. 1.5 C. 2 D. 3
4.如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA, OB
的中点M,N,测得MN=32 m,则A,B两点间的距离是( )
A.64 m B.16 m C.32 m D.24 m
( http: / / www.21cnjy.com )3题图 4题图 ( http: / / www.21cnjy.com )
5.对于反比例函数,下列说法不正确的是( )
A. 它的图象是双曲线并且在第一、三象限 B. 点(-4,)在它的图象上
C. 它的图象是中心对称图形 D. 随的增大而增大
6.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A. B. C. D.
7.若点(-2,y1)(-1,y2)、(1,y3)都在反比例函数(k<0)的图象上,则有( ).
A. y1>y2>y3 B. y2>y1>y3 C. y1>y3>y2 D. y3>y1>y2
8.两个相似三角形的相似比是2:3,其中较小的三角形的面积是12,则另一个三角形的面积是( )
A.8 B.16 C.24 D.27
9.在反比例函数的图象的每一条曲线上,y都随x的增大而增大,则k的值可以
是( )
A.2 B.1 C.0 D. -1
10抛物线的图象过原点,则为( )
.A0 B.1 C.-1 D.±1
11.如图,函数与(是非零常数)在同一坐标系中大致图象有可能是( )
12.已知直线y=ax(a≠0)与双曲线的一个交点坐标为(2,6),则它们的另一个交点坐标是( )
A. (﹣2,6) B. (﹣6,﹣2) C. (﹣2,﹣6) D. (6,2)
13.如图,路灯距地面8米,身高1.6米的 ( http: / / www.21cnjy.com )小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A、增大1.5米 B、减小1.5米 C、增大3.5米 D、减小3.5米
14.如图所示,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数y=k/x (x>0)的图象与△ABC有公共点,则k的取值范围是( ) ( http: / / www.21cnjy.com )14题图
A.2≤k≤9 B.2≤k≤8 C.2≤k≤5 D.5≤k≤8
15.如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①;②点F是GE的中点;③AF=AB;④S△ABC =5 S△BDF,其确的结论是________ ____.
A .①④ B.① ②③ C. ①③ D. ①②③④
第Ⅱ卷(非选择题 共75分)
注意事项:
1.第Ⅱ卷为非选择题,请考生用蓝、黑色钢笔(签字笔)或圆珠笔直接在试卷上作答.
2.答卷前,请考生先将考点、姓名、准考证号、座号填写在试卷规定的位置.
二、填空题(本大题共6个小题.每小题3分,共18分.把答案填在题中横线上.)
16.某数学兴趣小组测得小强的影长是1m, ( http: / / www.21cnjy.com )同一时刻旗杆的影长是15m.已知小强的身高为1.8m,则旗杆的高度为_________m..
17.在Rt△ABC中,∠C=90°,a=4,b=3,则sinA的值是 _________ ,
18.如图,E是 ABCD的边CD上一点,连接AE并延长交BC的延长线于点F,且AD=4,=,则CF的长为 ________ .
19.设函数与的图象的交点坐标为(a,b),则 的值为_________.
20 .二次函数y=x2-6x+n的部分图象如图所示,则它的对称轴为 x= .
21.如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点B,若,则的值为______.
( http: / / www.21cnjy.com )
得分 评卷人
三、解答题(本大题共6个小题,共57分.解答应写出文字说明,证明过程或演算步骤.)
22.计算(1) ﹣4cos45°+|﹣2|.(3分)
(2) 2-1-(π-2014)0+cos245°+tan30° sin60°(4分)
得分 评卷人
23. (7分) 如图,已知直线y=-x+4与反比例函数y=的图象相交于点A(-2,a),并且与x轴相交于点B。
(1)求a的值; (2)求反比例函数的表达式; (3)求△AOB的面积。
得分 评卷人
24.(8分)如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF
( http: / / www.21cnjy.com )
得分 评卷人
25.(8分)某数学活动小 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在B点测得C点的仰角为30°.已知山顶C点处的高度是600米.(1)求斜坡B点处的高度;(2)求斜坡AB的坡度.
( http: / / www.21cnjy.com )25题图
得分 评卷人
26.(9分)如图,在平面直角坐标系内 ( http: / / www.21cnjy.com ),已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
得分 评卷人
27.(9分) 如图,在直角梯形OABC中,BC//AO,∠AOC=900,点A、B的坐标分别为(5,0)、(2,6),点D为AB上一点,且BD=2AD.双曲线y=(x>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积。
28.(9分)在一个边长为a(单位:cm)的正方形ABCD中.
(1)如图1,如果N是AD中点,F为AB中点,连接DF,CN.
①求证:DF=CN;
②连接AC.则DH:HE: EF=_____________(直接写出结果)
(2)如图2,如果点E、M分别是线段AC、CD上的动点,假设点E从点A出发,以cm/s速度沿AC向点C运动,同时点M从点C出发,以1cm/s的速度沿CD向点D运动,运动时间为t(t>0),连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.。求证:当点F是边AB中点时,DM=2CM
九年级数学试题参考答案与评分标准(2014.11)
一、选择题 CACAD CBDAD BCDAC
二、填空
16. 27 17 4/5 18. 2 19. -1/2
20. 3 21. 6
三、解答题
22.(1)原式=2﹣4×+2=2.………………………3分
(2)原式=-1+( EQ \f(,2))2+ EQ \f(,3) EQ \f(,2)
=-1++
=…………………………4分
23解:(1)将A(-2,a)代入y=-x+4中,得:a=-(-2)+4,所以a=6----------- -2分
(2)由(1)得:A(-2,6)
将A(-2,6)代入y=中,得到:6=,即k=-12
所以反比例函数的表达式为:y=- ----------- 4分
(3)如图:过A点作AD⊥x轴于D;
∵A(-2,6),∴AD=6
在直线y=-x+4中,令y=0,得x=4
∴B(4,0),即OB=4
∴△AOB的面积S=OB×AD=×4×6=12.………….7分
24. 解:∵AB∥ CD
∴△ABE∽△CDE
∴AB:CD=BE:ED
∵AB=6cm,CD=12cm
∴AB:CD=1:2=BE:CD
∴BE:BD=1:3………………………..4分
∵EF∥CD
∴△BEF∽△BDC
∴EF:CD=BE:BD=1:3
∵CD=12cm ∴ EF=4cm………………8分
25 解:(1)如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足.(1分)
在B点测得C点的仰角为30°,
∴∠CBD=30°,又BC=400米,
∴CD=400×sin30°=400×=200(米).----------- 3分
∴B点的铅直高度为600﹣200=400(米).----------- 4分
(2)∵BE=400米,
∴AB=1040米,AE===960米,----------- -6分
∴AB的坡度iAB===,----------- -8分
26 解:(1)设直线AB的解析式为y=kx+b
由题意,得 解得
所以,直线AB的解析式为y=-x+6.………………………….4 分
(2)由AO=6, BO=8 得AB=10
所以AP=t ,AQ=10-2t
分两种情况:
1° 当∠APQ=∠AOB时,△APQ∽△AOB.
所以 = 解得 t=(秒) …………….6分
2° 当∠AQP=∠AOB时,△AQP∽△AOB.
所以 = 解得 t=(秒) ………………8分
∴t=秒或秒时,△APQ与△AOB相似…………………………….9分
27(1)①易证△ADF≌△DCN,则DF=CN;3分
②6:4:5 ……………………………………………………………5分
(2)过点E作EG⊥AD于点G,
依题意得,AE=,易求AG=EG=t,…………6分
CM=t,DG=DM=
易证△DGE≌△MDN,∴……….7分
由△ADF∽△DMN,得,
又∵点F是线段AB中点,AB=AD,
∴,
∴DM=2DN
∵DN=CM
∴DM=2CM………………………………………………………………………9分
28解:(1)过点B、D作x轴的的垂线,垂足分别为点M、N.
∵A (5.0)、B(2,6),∴OM=BC=2,BM=OC=6,AM=3.
∵DN∥BM,∴△AND∽△ABM.
∴
∴DN =2,AN=1, ∴ON=4
∴点D的坐标为(4,2).…………………………3分
又∵ 双曲线y=(x>0)经过点D,
∴k=2×4=8
∴双曲线的解析式为y=.………………………5分
(2)∵点E在BC上,∴点E的纵坐标为6.
又∵点E在双曲线y=上,
∴点E的坐标为(,6),∴CE=………………………7分
∴S四边形ODBE=S梯形OABC-S△OCE-S△AOD
=×(BC+OA)×OC-×OC×CE-×OA×DN
=×(2+5)×6-×6×-×5×2
=12
∴四边形ODBE的面积为12. ………………………………9分
装 订 线
班级 姓名 考场 考号 序号
第13题
第15题
x
O
P
y
A
Q
B
同课章节目录
