同角三角函数
图片预览






文档简介
课件16张PPT。同角三角函数的基本关系执教:浙江一级重点中学吕有红
2007.11.2 气象学家洛伦兹1963年提出一种观点:南美洲亚马逊河流域热带雨林中的一只蝴蝶,偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯的一场龙卷风。这就是理论界闻名的“蝴蝶效应”, 此效应本意是说事物初始条件的微弱变化可能会引起结果的巨大变化。蝴蝶扇翅膀成为龙卷风的导火索。从中我们还可以看出,南美洲亚马逊河流域热带雨林中的一只蝴蝶与北美德克萨斯的龙卷风看来是毫不相干的两种事物,却会有这样的联系,这也正验证了哲学理论中事物是普遍联系的观点。
既然感觉毫不相干的事物都是相互联系的,那么“同一个角”的三角函数一定会有非常密切的关系!到底是什么关系呢?这就是这节课的课题。
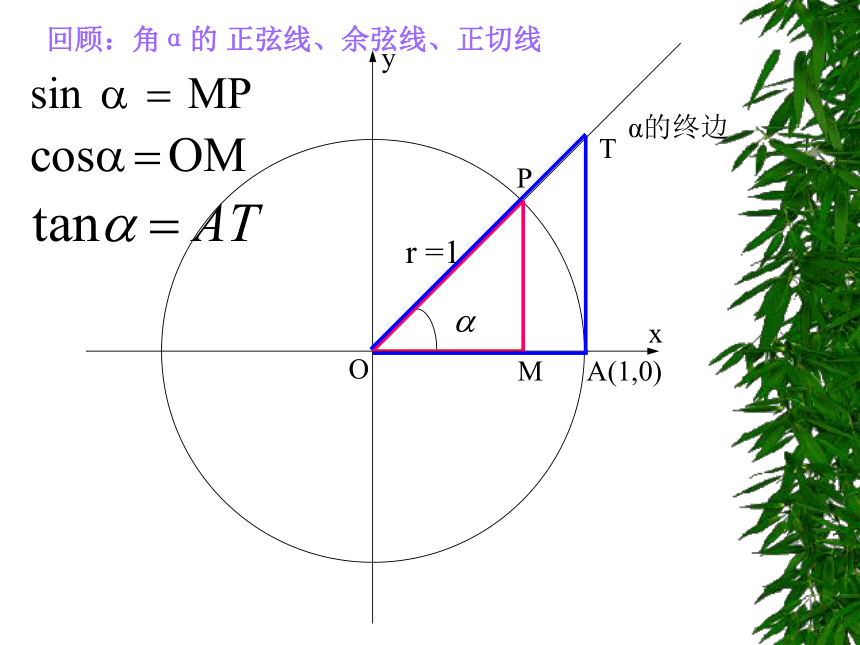
xyOPA(1,0)α的终边r =1回顾:角α的 正弦线、余弦线、正切线同角三角函数的基本关系式(平方关系)(商数关系) 探究:(1)对“同角”两字,大家是怎样理解的?(3)关系式有哪些转化形式?如: (2)这两个基本关系式中的角α有没有范围限制?( 4 )提问:若去掉“α是第二象限角”这个条件,结果是否一样?同步训练题:例2、求证:说明:证明恒等式的三种常用方法:
方法一:a=c, c=b a=b;
方法二:a=c, b=c a=b;
方法三:a=b c=d, 可先证 c=d例3 化简:练习:教材P20,T4(1)(2)提高题:(1)(2)2、解题时,注意角所在的象限,以确定三角
函数值符号;3、公式可作适当变形,注意灵活运用。小结:1、牢记两个基本关系式,并能用它求三角函
数值,化简三角函数式和三角恒等式的证明; 作业:
<<作业本A>>
P39 - P40
谢谢指导!
2007.11.2 气象学家洛伦兹1963年提出一种观点:南美洲亚马逊河流域热带雨林中的一只蝴蝶,偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯的一场龙卷风。这就是理论界闻名的“蝴蝶效应”, 此效应本意是说事物初始条件的微弱变化可能会引起结果的巨大变化。蝴蝶扇翅膀成为龙卷风的导火索。从中我们还可以看出,南美洲亚马逊河流域热带雨林中的一只蝴蝶与北美德克萨斯的龙卷风看来是毫不相干的两种事物,却会有这样的联系,这也正验证了哲学理论中事物是普遍联系的观点。
既然感觉毫不相干的事物都是相互联系的,那么“同一个角”的三角函数一定会有非常密切的关系!到底是什么关系呢?这就是这节课的课题。
xyOPA(1,0)α的终边r =1回顾:角α的 正弦线、余弦线、正切线同角三角函数的基本关系式(平方关系)(商数关系) 探究:(1)对“同角”两字,大家是怎样理解的?(3)关系式有哪些转化形式?如: (2)这两个基本关系式中的角α有没有范围限制?( 4 )提问:若去掉“α是第二象限角”这个条件,结果是否一样?同步训练题:例2、求证:说明:证明恒等式的三种常用方法:
方法一:a=c, c=b a=b;
方法二:a=c, b=c a=b;
方法三:a=b c=d, 可先证 c=d例3 化简:练习:教材P20,T4(1)(2)提高题:(1)(2)2、解题时,注意角所在的象限,以确定三角
函数值符号;3、公式可作适当变形,注意灵活运用。小结:1、牢记两个基本关系式,并能用它求三角函
数值,化简三角函数式和三角恒等式的证明; 作业:
<<作业本A>>
P39 - P40
谢谢指导!
