实际问题与一元二次方程(江苏省南通市海门市)
文档属性
| 名称 | 实际问题与一元二次方程(江苏省南通市海门市) |
|
|
| 格式 | rar | ||
| 文件大小 | 858.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-03 00:00:00 | ||
图片预览







文档简介
课件20张PPT。一元二次方程的应用(1)1、某工厂一月份生产零件1000个,二月份生产零件1200个,那么二月份比一月份增产 个,增长率是多少 。
2、某厂今年一月的产量为500吨,三月的产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=50020020%B3、剪一块面积是150cm2的长方形铁片,使它的长比宽
多5cm,如果设宽为xcm,可得方程为 。 x(x+5)=150 热身练习:例1、某超市一月份的营业额为200万元,第一季度的营业额为950万元,问二、三月份的平均增长率是多少? 解析:设月平均增长率为x,则二月份的产值是 ;三月份的产值是 。200(1+x)2200(1+x) 党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年(2001~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程是 。(1+x)2=4请你思考例2、有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人? 分析:开始有一人患了流感,第一轮的传染源就是这个人,
他传染了x个人,用代数式表示,第一轮后共有_____人患
了流感;第二轮传染中,这些人中的每个人又传染了x个人,
用代数式表示,第二轮后共有____________人患了流感.
于是可以得到方程 。(1+x)1+x+x(1+x)1+x+x(1+x)=121或者 (1+x)2=1213363练习:1、某种果树枝杈很多,它的主干长出若干数目的支干,每个支干又长出相同数目的小分支,主干、分支、小分支的总数是73.求每个支干长出多少个小分支?
2、九年级(2)班第二小组的同学每人都送给他人一张照片,全组共送了90张照片,若设这个小组共有x个人,则可列方程 人
3、假日里一些朋友聚会,又是握手,又是互换名片.如果他们共握手66次,若设有x人参加,则可列方程 人 1+x+x2=73x(x-1)=73x(x-1)=66×2你知道共送出多少张名片吗?小结 类似地 这种增长率的问题在实
际生活普遍存在,有一定的模式若平均增长(或降低)百分率为x,增长(或降低)前
的是a,增长(或降低)n次后的量是b,则它们的数
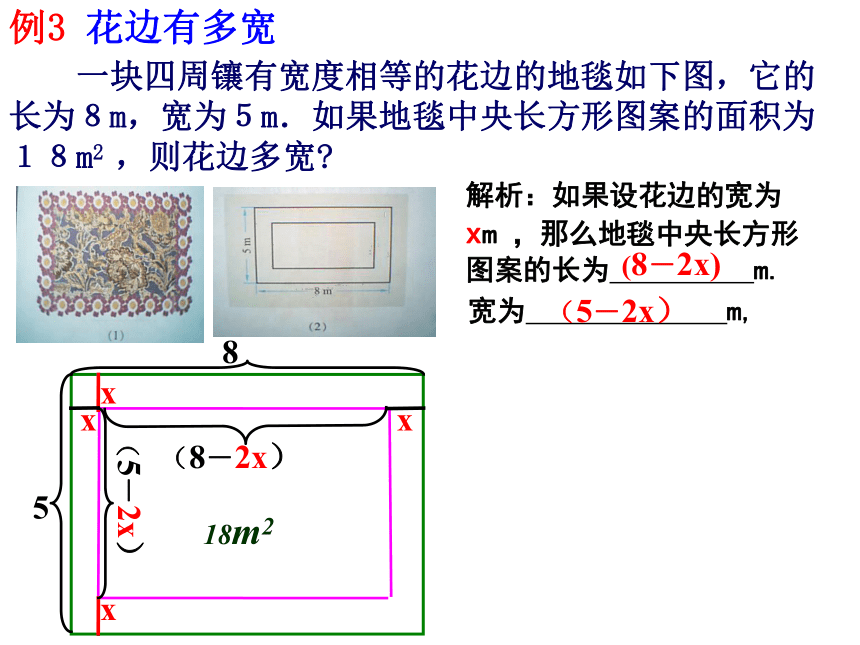
量关系可表示为:其中增长取+,降低取-5xxxx (8-2x)(5-2x)例3 花边有多宽 一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.如果地毯中央长方形图案的面积为18m2 ,则花边多宽?解析:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m. 宽为 m,(8-2x)(5-2x)18m28练习: 1、一桌面长6米,宽3米,铺在桌上的台布面积是桌面面积的3倍,并且各边垂下的长度相同,若设各边垂下的长度为x米,可得方程 。(6 + 2x) (3 + 2x) = 6×3×3 2、将一块正方形的铁皮四角剪去一个边长为4cm的小正方形,做成一个无盖的盒子.已知盒子的容积是400cm3,求原铁皮的边长. 4X-8练习: 3. 如图,在一块长92m,宽60m的矩形耕地上挖三条水渠,水渠的宽度都相等.水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽.练习:1、某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几?
2、课外植物小组准备利用学校仓库旁的一块空地,开辟一个面积为130平方米的花圃(如图),打算一面利用长为15米的仓库墙面,三面利用长为33米的旧围栏,求花圃的长和宽.设未知数,列方程课堂检测:练习:3.美化城市,改善人们的居住环境已成为城市建设的一项重要内容。某城市近几年来通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。(1)根据图中所提供的信息回答下列问题:2006年底的绿地面积为 公顷,比2005年底增加了 公顷;在2004年,2005年,2006年这三年中,绿地面积增加最多的是 ____________年;
(2)为满足城市发展的需要,计划到2008年底使城区绿地面积达到72.6公顷,试求2007年,2008年两年绿地面积的年平均增长率。6042005解:设2007年,2008年两年绿地面积的年平均增长率为x,根据题意,得
60 (1+x)2=72.6 .
(1+x)2=1.21.
∴1+x=±1.1.
∴ x1 = 0.1=10%,
x2 =-2.1(不合题意,舍去)
答: 2007年,2008年两年绿地面积的年平均增长率为10%.
你有什么收获?这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 列一元二次方程解应用题的步骤与
列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.小结拓展提高1、某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几?
2、在一块长16米、宽12米的矩形荒地上,建造一个花园,
使花园的所占面积为荒地面积的一半。你能给出设计方
案吗?
:(1)弄清题意和题目中的数量关系, 设未知数;
(2)找出能够表示应用题全部含义的一个相等关系;
(3)根据所找到的相等关系列出需要的代数式,从而列出方程;
(4)解所得到的方程,求出未知数的值;
(5)检验所求出的解,看它是否符合题意以确定问题的答案;
(6)写出答案(包括单位和名称)列方程解应用题的一般步骤审、设、列、解、验、答.
2、课外植物小组准备利用学校仓库旁的一块空地,开辟一个面积为130平方米的花圃(如图1-2-1),打算一面利用长为15米的仓库墙面,三面利用长为33米的旧围栏,求花圃的长和宽.3.(P58-8)某银行经过最近的两次降息,使一年期存款的年利率由2.25%降至1.98%,平均每次降息的百分率是多少(精确到0.01%)?总结:
1.两次增长后的量=原来的量(1+增长率)2
若原来为a,平均增长率是x,增长后的量为b
则 第1次增长后的量是a(1+x) =b
第2次增长后的量是a(1+x)2=b
……
第n次增长后的量是a(1+x)n=b
这就是重要的增长率公式.2、反之,若为两次降低,则
平均降低率公式为a(1-x)2=b
2、某厂今年一月的产量为500吨,三月的产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=50020020%B3、剪一块面积是150cm2的长方形铁片,使它的长比宽
多5cm,如果设宽为xcm,可得方程为 。 x(x+5)=150 热身练习:例1、某超市一月份的营业额为200万元,第一季度的营业额为950万元,问二、三月份的平均增长率是多少? 解析:设月平均增长率为x,则二月份的产值是 ;三月份的产值是 。200(1+x)2200(1+x) 党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年(2001~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程是 。(1+x)2=4请你思考例2、有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人? 分析:开始有一人患了流感,第一轮的传染源就是这个人,
他传染了x个人,用代数式表示,第一轮后共有_____人患
了流感;第二轮传染中,这些人中的每个人又传染了x个人,
用代数式表示,第二轮后共有____________人患了流感.
于是可以得到方程 。(1+x)1+x+x(1+x)1+x+x(1+x)=121或者 (1+x)2=1213363练习:1、某种果树枝杈很多,它的主干长出若干数目的支干,每个支干又长出相同数目的小分支,主干、分支、小分支的总数是73.求每个支干长出多少个小分支?
2、九年级(2)班第二小组的同学每人都送给他人一张照片,全组共送了90张照片,若设这个小组共有x个人,则可列方程 人
3、假日里一些朋友聚会,又是握手,又是互换名片.如果他们共握手66次,若设有x人参加,则可列方程 人 1+x+x2=73x(x-1)=73x(x-1)=66×2你知道共送出多少张名片吗?小结 类似地 这种增长率的问题在实
际生活普遍存在,有一定的模式若平均增长(或降低)百分率为x,增长(或降低)前
的是a,增长(或降低)n次后的量是b,则它们的数
量关系可表示为:其中增长取+,降低取-5xxxx (8-2x)(5-2x)例3 花边有多宽 一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.如果地毯中央长方形图案的面积为18m2 ,则花边多宽?解析:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m. 宽为 m,(8-2x)(5-2x)18m28练习: 1、一桌面长6米,宽3米,铺在桌上的台布面积是桌面面积的3倍,并且各边垂下的长度相同,若设各边垂下的长度为x米,可得方程 。(6 + 2x) (3 + 2x) = 6×3×3 2、将一块正方形的铁皮四角剪去一个边长为4cm的小正方形,做成一个无盖的盒子.已知盒子的容积是400cm3,求原铁皮的边长. 4X-8练习: 3. 如图,在一块长92m,宽60m的矩形耕地上挖三条水渠,水渠的宽度都相等.水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽.练习:1、某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几?
2、课外植物小组准备利用学校仓库旁的一块空地,开辟一个面积为130平方米的花圃(如图),打算一面利用长为15米的仓库墙面,三面利用长为33米的旧围栏,求花圃的长和宽.设未知数,列方程课堂检测:练习:3.美化城市,改善人们的居住环境已成为城市建设的一项重要内容。某城市近几年来通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。(1)根据图中所提供的信息回答下列问题:2006年底的绿地面积为 公顷,比2005年底增加了 公顷;在2004年,2005年,2006年这三年中,绿地面积增加最多的是 ____________年;
(2)为满足城市发展的需要,计划到2008年底使城区绿地面积达到72.6公顷,试求2007年,2008年两年绿地面积的年平均增长率。6042005解:设2007年,2008年两年绿地面积的年平均增长率为x,根据题意,得
60 (1+x)2=72.6 .
(1+x)2=1.21.
∴1+x=±1.1.
∴ x1 = 0.1=10%,
x2 =-2.1(不合题意,舍去)
答: 2007年,2008年两年绿地面积的年平均增长率为10%.
你有什么收获?这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 列一元二次方程解应用题的步骤与
列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.小结拓展提高1、某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几?
2、在一块长16米、宽12米的矩形荒地上,建造一个花园,
使花园的所占面积为荒地面积的一半。你能给出设计方
案吗?
:(1)弄清题意和题目中的数量关系, 设未知数;
(2)找出能够表示应用题全部含义的一个相等关系;
(3)根据所找到的相等关系列出需要的代数式,从而列出方程;
(4)解所得到的方程,求出未知数的值;
(5)检验所求出的解,看它是否符合题意以确定问题的答案;
(6)写出答案(包括单位和名称)列方程解应用题的一般步骤审、设、列、解、验、答.
2、课外植物小组准备利用学校仓库旁的一块空地,开辟一个面积为130平方米的花圃(如图1-2-1),打算一面利用长为15米的仓库墙面,三面利用长为33米的旧围栏,求花圃的长和宽.3.(P58-8)某银行经过最近的两次降息,使一年期存款的年利率由2.25%降至1.98%,平均每次降息的百分率是多少(精确到0.01%)?总结:
1.两次增长后的量=原来的量(1+增长率)2
若原来为a,平均增长率是x,增长后的量为b
则 第1次增长后的量是a(1+x) =b
第2次增长后的量是a(1+x)2=b
……
第n次增长后的量是a(1+x)n=b
这就是重要的增长率公式.2、反之,若为两次降低,则
平均降低率公式为a(1-x)2=b
同课章节目录
