2022-2023学年湖南省岳阳市平江县八年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年湖南省岳阳市平江县八年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 16:43:04 | ||
图片预览



文档简介
2022-2023学年湖南省岳阳市平江县八年级(下)期末数学试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,在中,,,则的度数为( )
A.
B.
C.
D.
2. 以下列各组数为边长,不能构成直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
3. 下列图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4. 菱形具有而矩形不一定具有的性质是( )
A. 对边平行 B. 对角线互相平分 C. 对角线互相垂直 D. 对角互补
5. 已知正比例函数的图象经过点,则的值为( )
A. B. C. D.
6. 若一次函数的图象经过点,,则与的大小关系是( )
A. B. C. D.
7. 函数中,自变量的取值范围是( )
A. B. C. D.
8. 若一个边形的内角和为,则的值是( )
A. B. C. D.
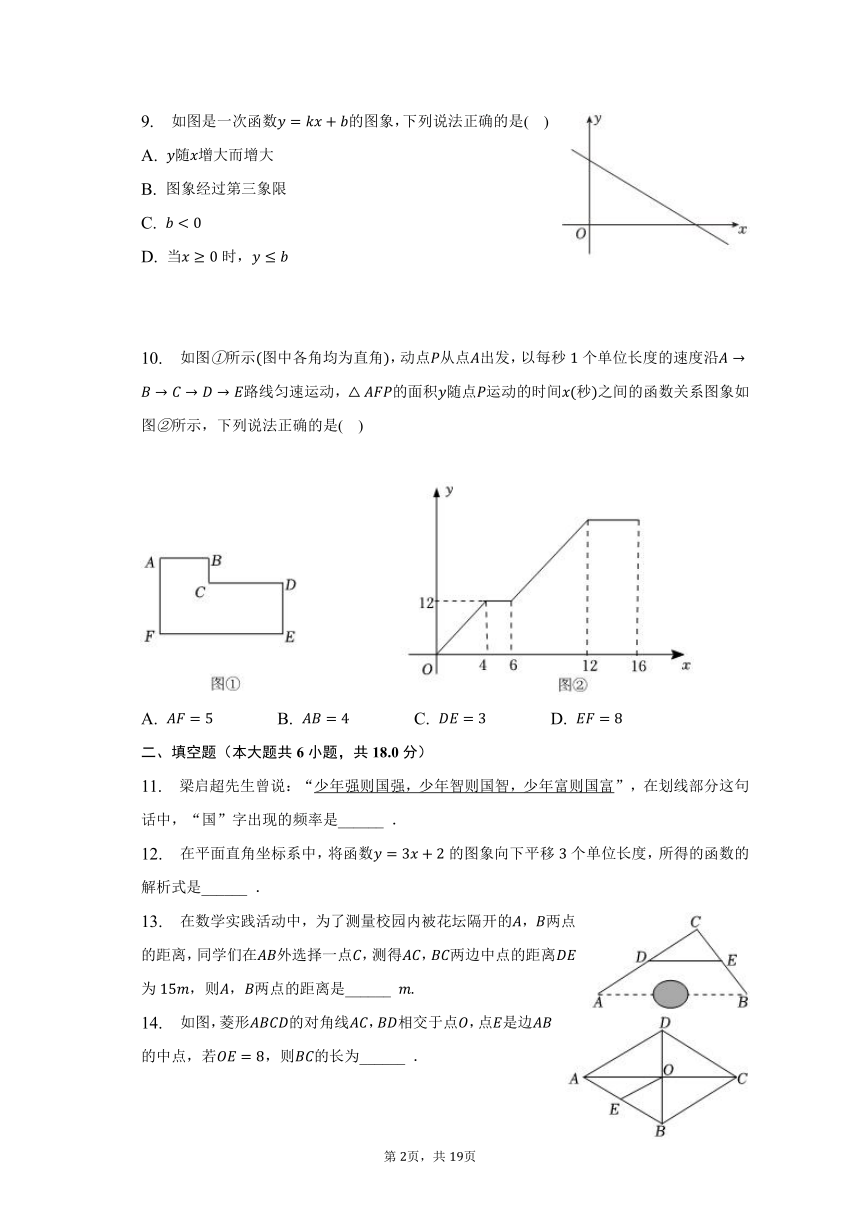
9. 如图是一次函数的图象,下列说法正确的是( )
A. 随增大而增大
B. 图象经过第三象限
C.
D. 当时,
10. 如图所示图中各角均为直角,动点从点出发,以每秒个单位长度的速度沿路线匀速运动,的面积随点运动的时间秒之间的函数关系图象如图所示,下列说法正确的是( )
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
11. 梁启超先生曾说:“少年强则国强,少年智则国智,少年富则国富”,在划线部分这句话中,“国”字出现的频率是______ .
12. 在平面直角坐标系中,将函数的图象向下平移个单位长度,所得的函数的解析式是______ .
13. 在数学实践活动中,为了测量校园内被花坛隔开的,两点的距离,同学们在外选择一点,测得,两边中点的距离为,则,两点的距离是______
14. 如图,菱形的对角线,相交于点,点是边的中点,若,则的长为______ .
15. 如图,在中,,是的平分线,于点,,,则 ______ .
16. 现代物流的高速发展,为乡村振兴提供了良好条件某物流公司的汽车行驶后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶到达目的地汽车行驶的时间单位:与行驶的路程单位:之间的关系如图所示.
前行驶速度是______ ;
高速路上行驶速度是______ .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,已知,、在线段上,与交于点,且,求证:≌.
18. 本小题分
为了调查某市噪音污染情况,该市环保局抽样调查了若干个噪声测量点的噪声声级,并根据、、、、、六个级别,绘制了两幅不完整的统计图:
此次抽样共调查了______ 个噪音测量点;
请把这幅频数分布直方图补充完整;画图后请标注相应数据
在扇形统计图中,噪声声级所对应的圆心角的度数为______
19. 本小题分
如图,图中的小方格都是边长为的正方形,的顶点坐标为 、 、 .
请在图中画出关于轴对称的图形;
写出点和的坐标.
20. 本小题分
在矩形中,对角线、相交于点,且、.
求证:;
若,,求矩形的面积.
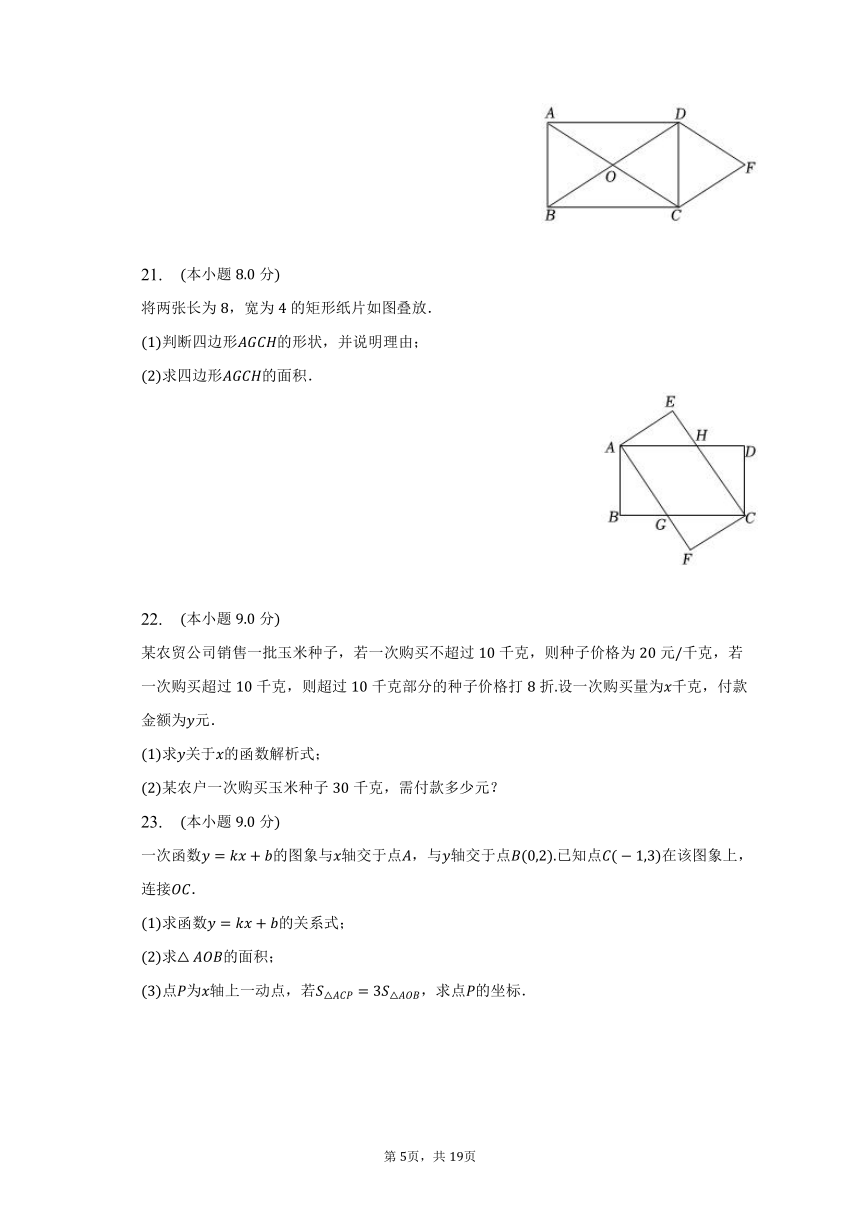
21. 本小题分
将两张长为,宽为的矩形纸片如图叠放.
判断四边形的形状,并说明理由;
求四边形的面积.
22. 本小题分
某农贸公司销售一批玉米种子,若一次购买不超过千克,则种子价格为元千克,若一次购买超过千克,则超过千克部分的种子价格打折设一次购买量为千克,付款金额为元.
求关于的函数解析式;
某农户一次购买玉米种子千克,需付款多少元?
23. 本小题分
一次函数的图象与轴交于点,与轴交于点已知点在该图象上,连接.
求函数的关系式;
求的面积;
点为轴上一动点,若,求点的坐标.
24. 本小题分
如图,点是正方形的边上的动点,,且,.
求证:;
若,,用表示的长.
25. 本小题分
在矩形中,,,点在线段上,点在线段上,且,连接,过点作,与边相交于点,与边相交于点,连接.
求线段的长;
求证:;
试探究线段,,三者之间的等量关系,并加以证明.
答案和解析
1.【答案】
【解析】解:在中,,
则,
,
,
故选:.
根据直角三角形的两锐角互余计算即可.
本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.
2.【答案】
【解析】解:、,符合勾股定理的逆定理,不符合题意;
B、,符合勾股定理的逆定理,不符合题意;
C、,符合勾股定理的逆定理,不符合题意;
D、,不符合勾股定理的逆定理,符合题意.
故选:.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
本题考查了勾股定理的逆定理,掌握理解勾股定理的逆定理是解题关键.
3.【答案】
【解析】解:不是中心对称图形,也不是轴对称图形,故此选项不合题意;
B.不是中心对称图形,是轴对称图形,故此选项不合题意;
C.不是中心对称图形,是轴对称图形,故此选项不合题意;
D.既是轴对称图形,又是中心对称图形,故此选项符合题意;
故选:.
根据中心对称图形与轴对称图形的概念,把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念,正确掌握相关定义是解题关键.
4.【答案】
【解析】解:对边平行,对角线互相平分是矩形,菱形都具有的性质,故A,不符合题意,
对角互补是矩形具有,而菱形不具有的性质,故D不符合题意;
菱形具有而矩形不一定具有的性质是对角线互相垂直,故C符合题意;
故选:.
根据矩形,菱形的性质即可解答.
本题考查矩形,菱形的性质,解题的关键是掌握矩形对角线相等,菱形对角线互相垂直.
5.【答案】
【解析】解:正比例函数的图象经过点,
,
解得:,
的值等于.
故选:.
由点的坐标,利用一次函数图象上点的坐标特征,可求出的值.
本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式”是解题的关键.
6.【答案】
【解析】解:,
随的增大而增大,
点,均在一次函数的图象上,且,
.
故选:.
由,利用一次函数图象的性质可得出随的增大而增大,结合,即可得出答案.
本题考查一次函数的图象与性质,牢记:在一次函数中,若,随的增大而增大;若,随的增大而减小.
7.【答案】
【解析】解:由题意得,
.
故选:.
由分母不等于求解即可.
本题考查了函数自变量的取值范围,函数有意义时字母的取值范围一般从几个方面考虑:当函数解析式是整式时,字母可取全体实数;当函数解析式是分式时,考虑分式的分母不能为;当函数解析式是二次根式时,被开方数为非负数.
8.【答案】
【解析】解:这个多边形的边数是,
则,
解得:.
故选:.
根据边形的内角和为列出关于的方程,解方程即可求出边数的值.
本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
9.【答案】
【解析】解:、由图象可得:随增大而减小,原说法错误,不符合题意;
B、图象不经过第三象限,原说法错误,不符合题意;
C、函数图象与轴的交点的纵坐标为,则,原说法错误,不符合题意;
D、由图象可得,当时,,正确,符合题意.
故选:.
根据一次函数的图象:从左往右逐渐下降,与轴交于正半轴,再逐项判断即可得.
本题考查的是一次函数的图象与性质,一次函数与坐标轴的交点坐标问题,能正确的识图是解本题的关键.
10.【答案】
【解析】
【分析】
本题主要考查了动点问题的函数图象,三角形的面积,结合图形与图象求出图形中的线段的长度是解题的关键.
利用图中的信息和三角形的面积公式分别求得图中的线段,由此选择出正确选项即可.
【解答】
解:解:由图的第一段折线可知:点经过秒到达点处,此时的三角形的面积为,
动点从点出发,以每秒个单位长度的速度沿路线匀速运动,
.
,
,
选项不正确,选项正确;
由图的第二段折线可知:点再经过秒到达点处,
,
由图的第三段折线可知:点再经过秒到达点处,
,
由图的第四段折线可知:点再经过秒到达点处,
.
选项不正确;
图中各角均为直角,
,
选项的结论不正确,
故选B.
11.【答案】
【解析】解:在“少年强则国强,少年智则国智,少年富则国富”这个字中,“国”字有个,
“国”字出现的频率是;
故答案为:.
先计算划线部分字的总数,再数“国”字个数,根据频率频数除以总数的定义即可得.
本题主要考查频数与频率,频率是指每个对象出现的次数与总次数的比值或者百分比,即频率频数数据总数.
12.【答案】
【解析】解:将一次函数的图象向下平移个单位长度,所得函数的表达式为,即.
故答案为:.
根据一次函数的平移规律:上加下减,左加右减解答即可.
本题考查了一次函数的图象与几何变换,掌握函数图象平移的规律是解题的关键.
13.【答案】
【解析】解:点、为,的中点,
为的中位线,
,
.
故答案为:.
根据题意得出为的中位线,然后利用其性质求解即可.
本题主要考查三角形中位线的判定和性质,熟练掌握三角形中位线的性质是解题关键.
14.【答案】
【解析】解:四边形是菱形,
,且,
又点是边的中点,
,
,
故答案为:.
根据四边形是菱形可知对角线相互垂直,四条边相等,由直角三角形斜边上的中线的性质得出,又由,即可求出.
此题主要考查菱形和直角三角形斜边上的中线的性质,熟练应用直角三角形斜边上的中线等于斜边的一半是解题的关键.
15.【答案】
【解析】解:,,,平分,
,
,
.
在中,.
故答案为:.
根据角平分线上的点到角两边的距离相等可得到,求解,再根据勾股定理解答即可.
此题主要考查的是勾股定理及角平分线的性质,关键是根据角平分线上的点到角两边的距离相等可得到.
16.【答案】
【解析】解:由图可知,前的行驶时间为,
前行驶速度是;
故答案为:;
汽车在乡村道路上行驶到达目的地,
汽车在时的行驶时间为,
汽车在高速路上行驶速度是.
故答案为:.
根据图得出前的行驶时间为,即可求出前行驶速度;
根据题意汽车在乡村道路上行驶到达目的地,汽车在高速路上行驶的时间,即可求出结果.
本题主要考查实际应用,解答本题的关键是正确确立出函数与图象的对应关系,属于基础题,要熟练掌握.
17.【答案】证明:,
,即,
,
与都为直角三角形,
在和中,,
≌.
【解析】由于与是直角三角形,根据直角三角形全等的判定的方法即可证明.
此题考查了直角三角形全等的判定,解题关键是由通过等量代换得到.
18.【答案】解:;
等级数量为个,
补全图形如下:
.
【解析】解:此次抽样共调查噪音测量点个,
故答案为:;
见答案;
在扇形统计图中,噪声声级所对应的圆心角的度数为,
故答案为:.
用等级数量除以其所占百分比即可;
根据个等级的频数之和为求出等级数量即可补全图形;
用乘以级数量所占比例即可.
此题考查了频数分布直方图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
19.【答案】解:关于轴对称的图形如图所示;
由图形可知,.
【解析】本题考查了轴对称变换的作图,属于基础题.
根据对称轴为轴,作出的轴对称图形;
根据所画出的图形,求点和的坐标.
20.【答案】证明:在和中,
,
≌,
,,
四边形是矩形,
,,
;
解:≌,,,
,,
又,
是等边三角形,,
,
四边形是矩形,
,
,
,
,
.
【解析】先证明≌得到,,再由矩形的性质证明,即可证明;
由全等三角形的性质得到,,即可证明是等边三角形,得到,求出的长即可得到答案.
本题主要考查了矩形的性质,勾股定理的应用,等边三角形的性质与判定,全等三角形的性质与判定,熟练掌握矩形的性质是解题的关键.
21.【答案】解:四边形是菱形,理由如下:
四边形和四边形是矩形,
,,,
四边形是平行四边形,
,,
,
平行四边形是菱形;
由可知,,
设,则,
在中,,
由勾股定理得:,
解得:,
,
.
【解析】由矩形的性质得,,,则四边形是平行四边形,再由平行四边形的性质得,即可得出结论;
设,则,在中,由勾股定理得出方程,解得,即可解决问题;
本题考查了矩形的性质,菱形的判定与性质,平行四边形的判定与性质,勾股定理等知识,熟练掌握矩形的性质和平行四边形的判定与性质是解题的关键.
22.【答案】解:根据题意,得
当时,;
当,;
把代入,
;
一次购买玉米种子千克,需付款元.
【解析】根据费用等于单价乘以数量,可以分别写出购买玉米种子数量不超过千克和超过千克时,关于的函数解析式;
将代入相应的函数解析式,即可得到需要付款多少元.
本题考查一次函数的应用,解答本题的关键是明确题意,确定费用的计算方法.
23.【答案】解:把、代入到中得:,
,
函数的解析式为;
把代入,
,即,
,
.
设点的坐标为,,,
,
,
,
,
或,
点的坐标为或.
【解析】把、代入到中进行求解即可;
先求解的坐标,再结合的坐标,直接利用三角形的面积公式进行计算即可;
设点的坐标为,根据得到,由此求解即可.
本题主要考查了一次函数与几何综合,坐标与图形的面积,求一次函数解析式,正确求出一次函数解析式是解题的关键.
24.【答案】证明:正方形,
,,
,
,,
,
,
,
在和中,
,
≌,
,,
,即;
连接,过作于,如图:
,
四边形是矩形,
由知:,
四边形是正方形,
,
,
,
中,,
.
【解析】由正方形,,,可得,,从而≌,可得,即可证明;
连接,过作于,证明四边形是正方形,可得,,即可在中,得.
本题考查正方形判定及性质,涉及全等三角形的判定与性质、勾股定理等知识,解题的关键是证明≌和四边形是正方形.
25.【答案】解:矩形,,,
,,,
;
证明:矩形,
,
,,
,,
,
≌,
.
证明:≌,
,连接,
,
为线段的垂直平分线,
.
在中,,
.
【解析】证明,,,再利用勾股定理可得答案;
证明,,,可得≌,可得;
利用≌,则,;利用线段垂直平分线的性质得到,再利用勾股定理即可得出结论.
本题考查的是全等三角形的判定与性质,勾股定理的应用,线段的垂直平分线的性质,矩形的性质,掌握以上基础知识是解本题的关键.
第1页,共1页
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,在中,,,则的度数为( )
A.
B.
C.
D.
2. 以下列各组数为边长,不能构成直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
3. 下列图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4. 菱形具有而矩形不一定具有的性质是( )
A. 对边平行 B. 对角线互相平分 C. 对角线互相垂直 D. 对角互补
5. 已知正比例函数的图象经过点,则的值为( )
A. B. C. D.
6. 若一次函数的图象经过点,,则与的大小关系是( )
A. B. C. D.
7. 函数中,自变量的取值范围是( )
A. B. C. D.
8. 若一个边形的内角和为,则的值是( )
A. B. C. D.
9. 如图是一次函数的图象,下列说法正确的是( )
A. 随增大而增大
B. 图象经过第三象限
C.
D. 当时,
10. 如图所示图中各角均为直角,动点从点出发,以每秒个单位长度的速度沿路线匀速运动,的面积随点运动的时间秒之间的函数关系图象如图所示,下列说法正确的是( )
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
11. 梁启超先生曾说:“少年强则国强,少年智则国智,少年富则国富”,在划线部分这句话中,“国”字出现的频率是______ .
12. 在平面直角坐标系中,将函数的图象向下平移个单位长度,所得的函数的解析式是______ .
13. 在数学实践活动中,为了测量校园内被花坛隔开的,两点的距离,同学们在外选择一点,测得,两边中点的距离为,则,两点的距离是______
14. 如图,菱形的对角线,相交于点,点是边的中点,若,则的长为______ .
15. 如图,在中,,是的平分线,于点,,,则 ______ .
16. 现代物流的高速发展,为乡村振兴提供了良好条件某物流公司的汽车行驶后进入高速路,在高速路上匀速行驶一段时间后,再在乡村道路上行驶到达目的地汽车行驶的时间单位:与行驶的路程单位:之间的关系如图所示.
前行驶速度是______ ;
高速路上行驶速度是______ .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,已知,、在线段上,与交于点,且,求证:≌.
18. 本小题分
为了调查某市噪音污染情况,该市环保局抽样调查了若干个噪声测量点的噪声声级,并根据、、、、、六个级别,绘制了两幅不完整的统计图:
此次抽样共调查了______ 个噪音测量点;
请把这幅频数分布直方图补充完整;画图后请标注相应数据
在扇形统计图中,噪声声级所对应的圆心角的度数为______
19. 本小题分
如图,图中的小方格都是边长为的正方形,的顶点坐标为 、 、 .
请在图中画出关于轴对称的图形;
写出点和的坐标.
20. 本小题分
在矩形中,对角线、相交于点,且、.
求证:;
若,,求矩形的面积.
21. 本小题分
将两张长为,宽为的矩形纸片如图叠放.
判断四边形的形状,并说明理由;
求四边形的面积.
22. 本小题分
某农贸公司销售一批玉米种子,若一次购买不超过千克,则种子价格为元千克,若一次购买超过千克,则超过千克部分的种子价格打折设一次购买量为千克,付款金额为元.
求关于的函数解析式;
某农户一次购买玉米种子千克,需付款多少元?
23. 本小题分
一次函数的图象与轴交于点,与轴交于点已知点在该图象上,连接.
求函数的关系式;
求的面积;
点为轴上一动点,若,求点的坐标.
24. 本小题分
如图,点是正方形的边上的动点,,且,.
求证:;
若,,用表示的长.
25. 本小题分
在矩形中,,,点在线段上,点在线段上,且,连接,过点作,与边相交于点,与边相交于点,连接.
求线段的长;
求证:;
试探究线段,,三者之间的等量关系,并加以证明.
答案和解析
1.【答案】
【解析】解:在中,,
则,
,
,
故选:.
根据直角三角形的两锐角互余计算即可.
本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.
2.【答案】
【解析】解:、,符合勾股定理的逆定理,不符合题意;
B、,符合勾股定理的逆定理,不符合题意;
C、,符合勾股定理的逆定理,不符合题意;
D、,不符合勾股定理的逆定理,符合题意.
故选:.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
本题考查了勾股定理的逆定理,掌握理解勾股定理的逆定理是解题关键.
3.【答案】
【解析】解:不是中心对称图形,也不是轴对称图形,故此选项不合题意;
B.不是中心对称图形,是轴对称图形,故此选项不合题意;
C.不是中心对称图形,是轴对称图形,故此选项不合题意;
D.既是轴对称图形,又是中心对称图形,故此选项符合题意;
故选:.
根据中心对称图形与轴对称图形的概念,把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念,正确掌握相关定义是解题关键.
4.【答案】
【解析】解:对边平行,对角线互相平分是矩形,菱形都具有的性质,故A,不符合题意,
对角互补是矩形具有,而菱形不具有的性质,故D不符合题意;
菱形具有而矩形不一定具有的性质是对角线互相垂直,故C符合题意;
故选:.
根据矩形,菱形的性质即可解答.
本题考查矩形,菱形的性质,解题的关键是掌握矩形对角线相等,菱形对角线互相垂直.
5.【答案】
【解析】解:正比例函数的图象经过点,
,
解得:,
的值等于.
故选:.
由点的坐标,利用一次函数图象上点的坐标特征,可求出的值.
本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式”是解题的关键.
6.【答案】
【解析】解:,
随的增大而增大,
点,均在一次函数的图象上,且,
.
故选:.
由,利用一次函数图象的性质可得出随的增大而增大,结合,即可得出答案.
本题考查一次函数的图象与性质,牢记:在一次函数中,若,随的增大而增大;若,随的增大而减小.
7.【答案】
【解析】解:由题意得,
.
故选:.
由分母不等于求解即可.
本题考查了函数自变量的取值范围,函数有意义时字母的取值范围一般从几个方面考虑:当函数解析式是整式时,字母可取全体实数;当函数解析式是分式时,考虑分式的分母不能为;当函数解析式是二次根式时,被开方数为非负数.
8.【答案】
【解析】解:这个多边形的边数是,
则,
解得:.
故选:.
根据边形的内角和为列出关于的方程,解方程即可求出边数的值.
本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
9.【答案】
【解析】解:、由图象可得:随增大而减小,原说法错误,不符合题意;
B、图象不经过第三象限,原说法错误,不符合题意;
C、函数图象与轴的交点的纵坐标为,则,原说法错误,不符合题意;
D、由图象可得,当时,,正确,符合题意.
故选:.
根据一次函数的图象:从左往右逐渐下降,与轴交于正半轴,再逐项判断即可得.
本题考查的是一次函数的图象与性质,一次函数与坐标轴的交点坐标问题,能正确的识图是解本题的关键.
10.【答案】
【解析】
【分析】
本题主要考查了动点问题的函数图象,三角形的面积,结合图形与图象求出图形中的线段的长度是解题的关键.
利用图中的信息和三角形的面积公式分别求得图中的线段,由此选择出正确选项即可.
【解答】
解:解:由图的第一段折线可知:点经过秒到达点处,此时的三角形的面积为,
动点从点出发,以每秒个单位长度的速度沿路线匀速运动,
.
,
,
选项不正确,选项正确;
由图的第二段折线可知:点再经过秒到达点处,
,
由图的第三段折线可知:点再经过秒到达点处,
,
由图的第四段折线可知:点再经过秒到达点处,
.
选项不正确;
图中各角均为直角,
,
选项的结论不正确,
故选B.
11.【答案】
【解析】解:在“少年强则国强,少年智则国智,少年富则国富”这个字中,“国”字有个,
“国”字出现的频率是;
故答案为:.
先计算划线部分字的总数,再数“国”字个数,根据频率频数除以总数的定义即可得.
本题主要考查频数与频率,频率是指每个对象出现的次数与总次数的比值或者百分比,即频率频数数据总数.
12.【答案】
【解析】解:将一次函数的图象向下平移个单位长度,所得函数的表达式为,即.
故答案为:.
根据一次函数的平移规律:上加下减,左加右减解答即可.
本题考查了一次函数的图象与几何变换,掌握函数图象平移的规律是解题的关键.
13.【答案】
【解析】解:点、为,的中点,
为的中位线,
,
.
故答案为:.
根据题意得出为的中位线,然后利用其性质求解即可.
本题主要考查三角形中位线的判定和性质,熟练掌握三角形中位线的性质是解题关键.
14.【答案】
【解析】解:四边形是菱形,
,且,
又点是边的中点,
,
,
故答案为:.
根据四边形是菱形可知对角线相互垂直,四条边相等,由直角三角形斜边上的中线的性质得出,又由,即可求出.
此题主要考查菱形和直角三角形斜边上的中线的性质,熟练应用直角三角形斜边上的中线等于斜边的一半是解题的关键.
15.【答案】
【解析】解:,,,平分,
,
,
.
在中,.
故答案为:.
根据角平分线上的点到角两边的距离相等可得到,求解,再根据勾股定理解答即可.
此题主要考查的是勾股定理及角平分线的性质,关键是根据角平分线上的点到角两边的距离相等可得到.
16.【答案】
【解析】解:由图可知,前的行驶时间为,
前行驶速度是;
故答案为:;
汽车在乡村道路上行驶到达目的地,
汽车在时的行驶时间为,
汽车在高速路上行驶速度是.
故答案为:.
根据图得出前的行驶时间为,即可求出前行驶速度;
根据题意汽车在乡村道路上行驶到达目的地,汽车在高速路上行驶的时间,即可求出结果.
本题主要考查实际应用,解答本题的关键是正确确立出函数与图象的对应关系,属于基础题,要熟练掌握.
17.【答案】证明:,
,即,
,
与都为直角三角形,
在和中,,
≌.
【解析】由于与是直角三角形,根据直角三角形全等的判定的方法即可证明.
此题考查了直角三角形全等的判定,解题关键是由通过等量代换得到.
18.【答案】解:;
等级数量为个,
补全图形如下:
.
【解析】解:此次抽样共调查噪音测量点个,
故答案为:;
见答案;
在扇形统计图中,噪声声级所对应的圆心角的度数为,
故答案为:.
用等级数量除以其所占百分比即可;
根据个等级的频数之和为求出等级数量即可补全图形;
用乘以级数量所占比例即可.
此题考查了频数分布直方图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
19.【答案】解:关于轴对称的图形如图所示;
由图形可知,.
【解析】本题考查了轴对称变换的作图,属于基础题.
根据对称轴为轴,作出的轴对称图形;
根据所画出的图形,求点和的坐标.
20.【答案】证明:在和中,
,
≌,
,,
四边形是矩形,
,,
;
解:≌,,,
,,
又,
是等边三角形,,
,
四边形是矩形,
,
,
,
,
.
【解析】先证明≌得到,,再由矩形的性质证明,即可证明;
由全等三角形的性质得到,,即可证明是等边三角形,得到,求出的长即可得到答案.
本题主要考查了矩形的性质,勾股定理的应用,等边三角形的性质与判定,全等三角形的性质与判定,熟练掌握矩形的性质是解题的关键.
21.【答案】解:四边形是菱形,理由如下:
四边形和四边形是矩形,
,,,
四边形是平行四边形,
,,
,
平行四边形是菱形;
由可知,,
设,则,
在中,,
由勾股定理得:,
解得:,
,
.
【解析】由矩形的性质得,,,则四边形是平行四边形,再由平行四边形的性质得,即可得出结论;
设,则,在中,由勾股定理得出方程,解得,即可解决问题;
本题考查了矩形的性质,菱形的判定与性质,平行四边形的判定与性质,勾股定理等知识,熟练掌握矩形的性质和平行四边形的判定与性质是解题的关键.
22.【答案】解:根据题意,得
当时,;
当,;
把代入,
;
一次购买玉米种子千克,需付款元.
【解析】根据费用等于单价乘以数量,可以分别写出购买玉米种子数量不超过千克和超过千克时,关于的函数解析式;
将代入相应的函数解析式,即可得到需要付款多少元.
本题考查一次函数的应用,解答本题的关键是明确题意,确定费用的计算方法.
23.【答案】解:把、代入到中得:,
,
函数的解析式为;
把代入,
,即,
,
.
设点的坐标为,,,
,
,
,
,
或,
点的坐标为或.
【解析】把、代入到中进行求解即可;
先求解的坐标,再结合的坐标,直接利用三角形的面积公式进行计算即可;
设点的坐标为,根据得到,由此求解即可.
本题主要考查了一次函数与几何综合,坐标与图形的面积,求一次函数解析式,正确求出一次函数解析式是解题的关键.
24.【答案】证明:正方形,
,,
,
,,
,
,
,
在和中,
,
≌,
,,
,即;
连接,过作于,如图:
,
四边形是矩形,
由知:,
四边形是正方形,
,
,
,
中,,
.
【解析】由正方形,,,可得,,从而≌,可得,即可证明;
连接,过作于,证明四边形是正方形,可得,,即可在中,得.
本题考查正方形判定及性质,涉及全等三角形的判定与性质、勾股定理等知识,解题的关键是证明≌和四边形是正方形.
25.【答案】解:矩形,,,
,,,
;
证明:矩形,
,
,,
,,
,
≌,
.
证明:≌,
,连接,
,
为线段的垂直平分线,
.
在中,,
.
【解析】证明,,,再利用勾股定理可得答案;
证明,,,可得≌,可得;
利用≌,则,;利用线段垂直平分线的性质得到,再利用勾股定理即可得出结论.
本题考查的是全等三角形的判定与性质,勾股定理的应用,线段的垂直平分线的性质,矩形的性质,掌握以上基础知识是解本题的关键.
第1页,共1页
同课章节目录
