第五章功和简单机械章节测评卷-2023-2024学年华东师大版科学九年级上册(含答案)
文档属性
| 名称 | 第五章功和简单机械章节测评卷-2023-2024学年华东师大版科学九年级上册(含答案) | 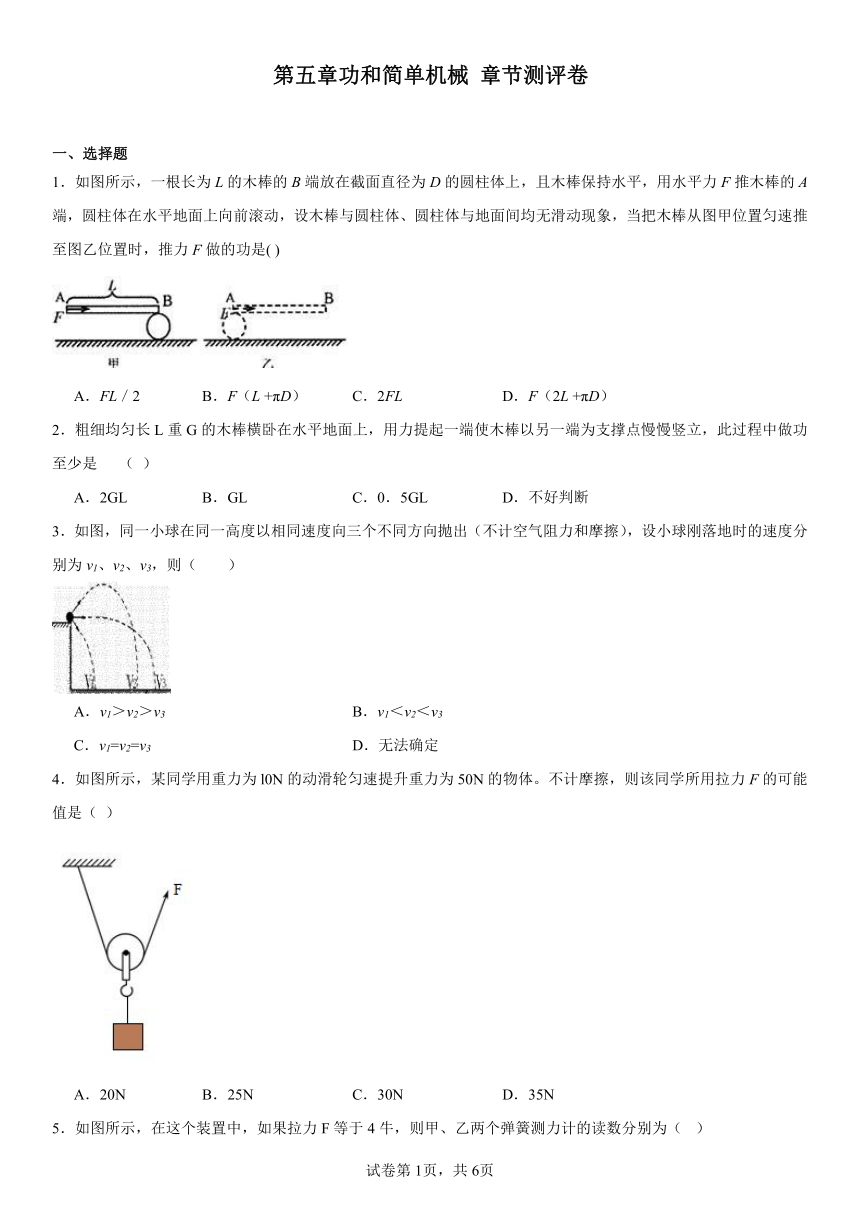 | |
| 格式 | docx | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-08-29 17:14:46 | ||
图片预览



文档简介
第五章功和简单机械 章节测评卷
一、选择题
1.如图所示,一根长为L的木棒的B端放在截面直径为D的圆柱体上,且木棒保持水平,用水平力F推木棒的A端,圆柱体在水平地面上向前滚动,设木棒与圆柱体、圆柱体与地面间均无滑动现象,当把木棒从图甲位置匀速推至图乙位置时,推力F做的功是( )
A.FL/2 B.F(L +πD) C.2FL D.F(2L +πD)
2.粗细均匀长L重G的木棒横卧在水平地面上,用力提起一端使木棒以另一端为支撑点慢慢竖立,此过程中做功至少是 ( )
A.2GL B.GL C.0.5GL D.不好判断
3.如图,同一小球在同一高度以相同速度向三个不同方向抛出(不计空气阻力和摩擦),设小球刚落地时的速度分别为v1、v2、v3,则( )
A.v1>v2>v3 B.v1<v2<v3
C.v1=v2=v3 D.无法确定
4.如图所示,某同学用重力为l0N的动滑轮匀速提升重力为50N的物体。不计摩擦,则该同学所用拉力F的可能值是( )
A.20N B.25N C.30N D.35N
5.如图所示,在这个装置中,如果拉力F等于4牛,则甲、乙两个弹簧测力计的读数分别为( )
A.8牛,l2牛 B.12牛,8牛
C.8牛,8牛 D.12牛,l2牛
6.下列说法正确的是( )
A.机械的功率越大,机械工作时做功越快
B.机械的功率越大,机械工作时能量转化越多
C.机械的功率越大,机械效率越高
D.一切具有做功本领的物体,是因为它具有机械能
7.质量是6kg的物体A放在水平桌面上,利用图所示的装置使物体以0.2m/s的速度做匀速直线运动,弹簧测力计始终保持水平,其示数为2N,不计绳子的伸长和滑轮组内部的摩擦,则( )
A.作用在绳端的拉力F为6N
B.水平桌面对物体a的摩擦力是2N
C.在1s内拉力F做功1.2J
D.拉力F的功率是0.4W
8.由五块相同砖块构成的桥,如图所示,若每块砖长度为30厘米,则此桥的最大跨度L为( )
A.20厘米 B.30厘米 C.40厘米 D.50厘米
9.人在踮脚时主要靠腓肠肌收缩,如图所示,若某人的重量
为500牛,MO=2N0,则双脚同时踮起时,每只脚的腓肠肌的作用力是( )
A.250牛 B.125牛 C.500牛 D.1000牛
10.如图,AB是一个略向左下倾斜的轨道,轨道由两根小木棒组成,两根小木棒在A端的距离大,B端的距离小。现将一个两头尖,中间大的由C处自由释放,则我们可以观察到的现象( )
A.滚动体向高处A端滚动
B.滚动体向低处B端滚动
C.滚动体停在C处不动
D.以上三种情况都有可能发生
11.如图所示杠杆提升重物G,力F顺时针方向转动,并使杠杆始终在图示位置平衡,则力F的大小将
A.逐渐变小 B.先变小,再变大
C.先变大,再变小 D.逐渐变大
12.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中( )
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确
B.只有②③正确
C.只有①②正确
D.只有③④正确
二、填空题
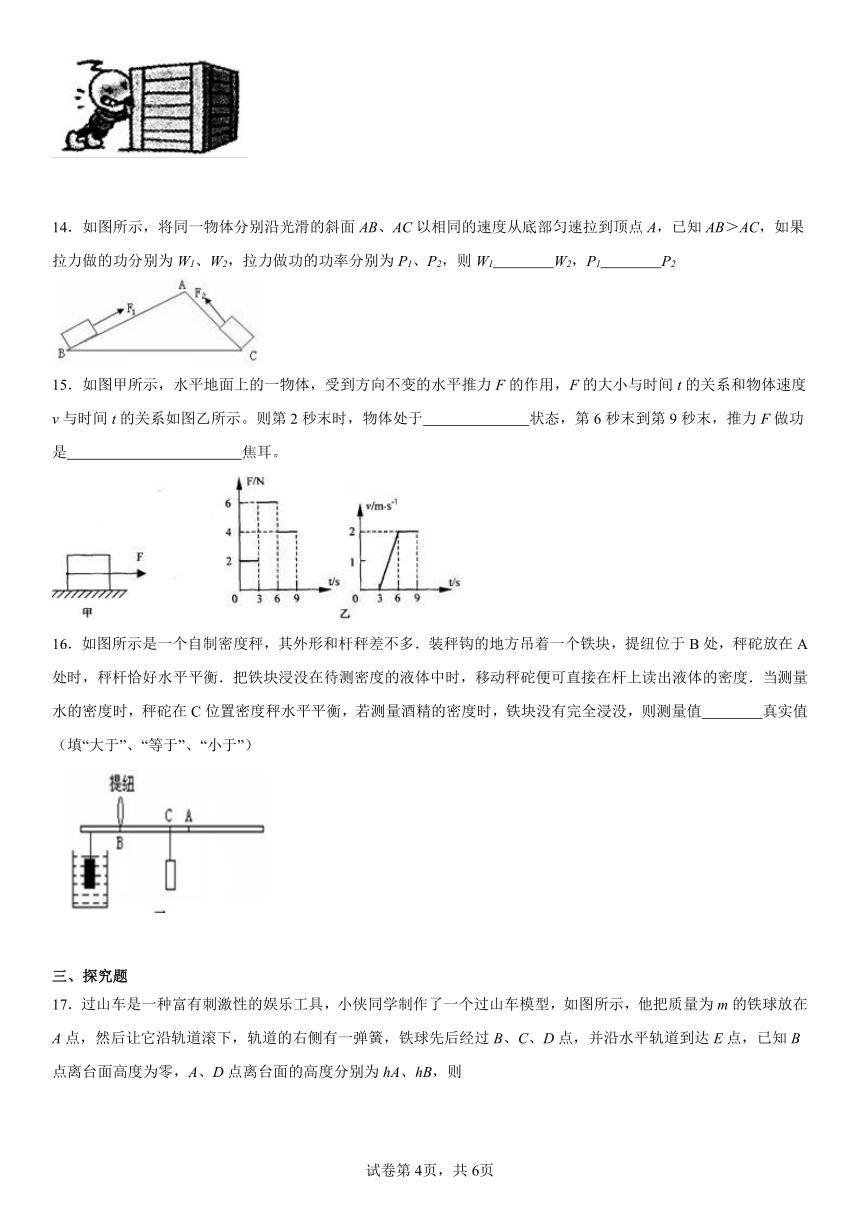
13.如图所示,用水平力推水平地面上的大木箱,并向前做匀速直线运动。这时,木箱受到的推力 摩擦力(填“大于”“等于”“小于”),大木箱的机械能 (填“增大”“不变”“减小”)。
14.如图所示,将同一物体分别沿光滑的斜面AB、AC以相同的速度从底部匀速拉到顶点A,已知AB>AC,如果拉力做的功分别为W1、W2,拉力做功的功率分别为P1、P2,则W1 W2,P1 P2
15.如图甲所示,水平地面上的一物体,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体速度v与时间t的关系如图乙所示。则第2秒末时,物体处于 状态,第6秒末到第9秒末,推力F做功是 焦耳。
16.如图所示是一个自制密度秤,其外形和杆秤差不多.装秤钩的地方吊着一个铁块,提纽位于B处,秤砣放在A处时,秤杆恰好水平平衡.把铁块浸没在待测密度的液体中时,移动秤砣便可直接在杆上读出液体的密度.当测量水的密度时,秤砣在C位置密度秤水平平衡,若测量酒精的密度时,铁块没有完全浸没,则测量值 真实值(填“大于”、“等于”、“小于”)
三、探究题
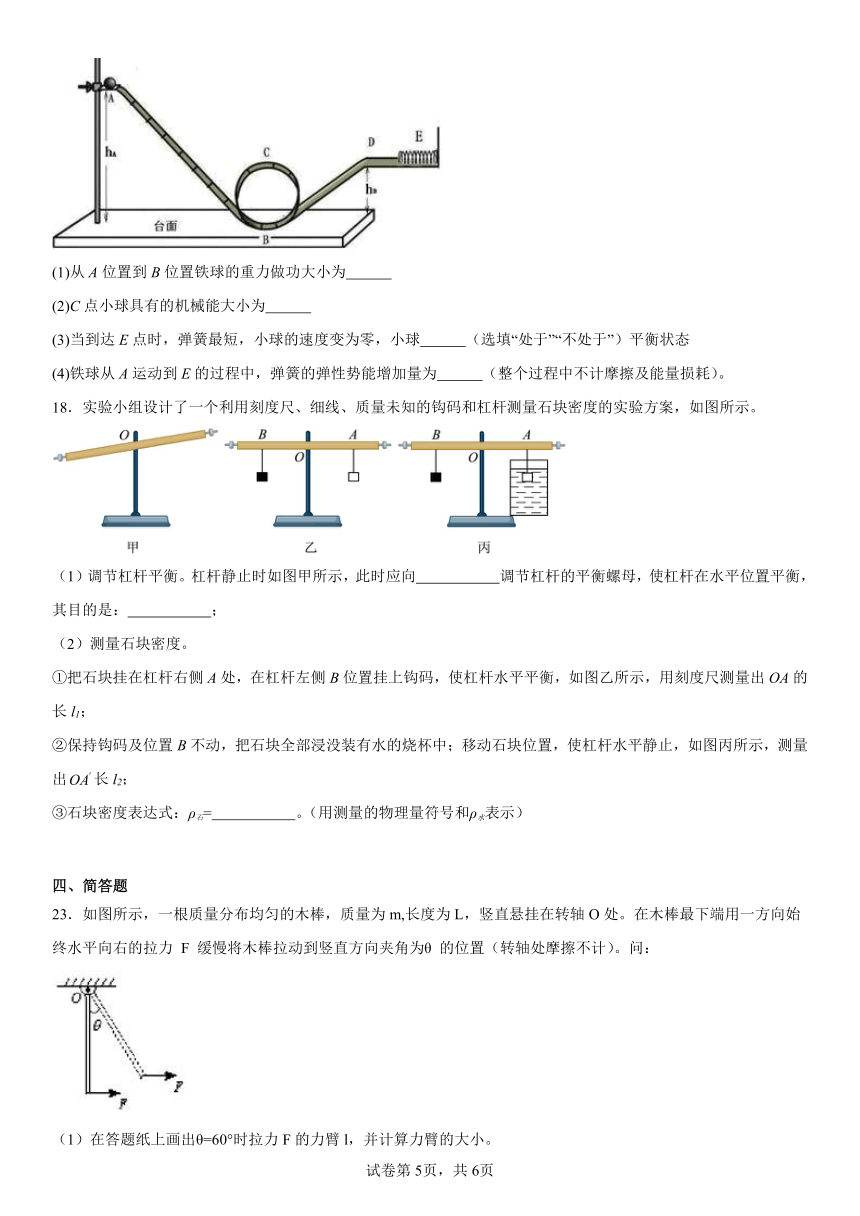
17.过山车是一种富有刺激性的娱乐工具,小侠同学制作了一个过山车模型,如图所示,他把质量为m的铁球放在A点,然后让它沿轨道滚下,轨道的右侧有一弹簧,铁球先后经过B、C、D点,并沿水平轨道到达E点,已知B点离台面高度为零,A、D点离台面的高度分别为hA、hB,则
(1)从A位置到B位置铁球的重力做功大小为
(2)C点小球具有的机械能大小为
(3)当到达E点时,弹簧最短,小球的速度变为零,小球 (选填“处于”“不处于”)平衡状态
(4)铁球从A运动到E的过程中,弹簧的弹性势能增加量为 (整个过程中不计摩擦及能量损耗)。
18.实验小组设计了一个利用刻度尺、细线、质量未知的钩码和杠杆测量石块密度的实验方案,如图所示。
(1)调节杠杆平衡。杠杆静止时如图甲所示,此时应向 调节杠杆的平衡螺母,使杠杆在水平位置平衡,其目的是: ;
(2)测量石块密度。
①把石块挂在杠杆右侧A处,在杠杆左侧B位置挂上钩码,使杠杆水平平衡,如图乙所示,用刻度尺测量出OA的长l1;
②保持钩码及位置B不动,把石块全部浸没装有水的烧杯中;移动石块位置,使杠杆水平静止,如图丙所示,测量出长l2;
③石块密度表达式:ρ石= 。(用测量的物理量符号和ρ水表示)
四、简答题
23.如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力 F 缓慢将木棒拉动到竖直方向夹角为θ 的位置(转轴处摩擦不计)。问:
(1)在答题纸上画出θ=60°时拉力F的力臂l,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?
并推导拉力F与角度θ的关系式。
24.为探究平衡木受力特点,喜爱体操的小薇设计了一个平衡木模型。整个装置如图甲所示AB可绕支点O无摩擦转动,C处固定一竖直硬杆,硬杆的底部安装了压敏电阻片R,R所在的电路放在了硬杆内(整个装置除硬杆以外,其他部分的重力均不计),且AB=5m,OA=BC=1m,电源电压恒为3V,硬杆底部R阻值随地面对它的支持力F变化的关系如图乙所示,整个装置放在水平地面上,AB始终处于水平平衡状态,当重360N的小薇站在A点时,电流表的示数为0.1A,求:
(1)小薇在A点时,C处受到硬杆的拉力;
(2)小薇在A点时,地面对硬杆底部R的支持力;
(3)当电流表的示数为0.3A时,小薇距A点多少米
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】力F做功可以看成:对木板做的功加上对球做的功:对木板做的功:位移s1等于木板的长度L,由W=Fs,得W1=FL;
再看对球做的功:木板和球、球和地面没有滑动摩擦,只有滚动摩擦,所以球的位移s2就等于球转动的圈数,球转动的圈数又等于木板的长度L;由于推动过程是匀速运动,所以木板和球的受力都是平衡的,木板的推力F等于球对木板的摩擦力,木板对球和球对木板的摩擦力是一对相互作用力,两力是相等的,所以球受到的力也为F;由W=Fs,得 W2=FL;所以F做得总功 W=W1+W2=2FL,故C正确。
2.C
【分析】既然是均匀的木棒,那重心就在木棒中点的地方,那么用力提起一端使木棒以另一端为支撑点慢慢竖立起来,木棒的重心从水平到垂直的距离h=L,然后利用W=Gh即可得出答案.
【详解】由于木棒质地均匀,那么木棒的重心位于木棒的中点处;木棒由水平到竖立的过程中,重心移动了h=L;那么要想提起这根木棒,至少要做的功为W=Gh=G L=0.5GL.
故选C.
3.C
【详解】小球从抛出到落地,发生了重力势能和动能的转化;在不计空气阻力和摩擦的条件下,转化过程中,机械能守恒,即机械能的总和不变。小球抛出时的机械能与小球落地时的机械能相等;而小球落地时的势能为零,故机械能大小就是动能大小,即动能相等所以速度相同。
故选C。
4.D
【详解】由题图可知:拉力F的方向不是竖直向上的,则力F的力臂将不再是动滑轮的直径,而是小于直径,如图所示:
根据杠杆的平衡条件得:
因为,所以:
即:
故D项符合题意、ABC项不符合题意。
故选D。
5.B
【详解】绳子静止,根据二力平衡,绳子两头的拉力是相等的,每根绳子的拉力都是4N;弹簧秤甲的拉力由三段绳子来承担,每根绳子的拉力大小都是4N,所以甲的读数是12N;弹簧秤乙的拉力由两段绳子来承担,每根绳子的拉力大小都是4N,所以乙的读数是8N.
6.A
【详解】A. 机械功率大表明机械做功快,故A正确。
B. 机械的功率越大,机械做功越快,使用机械做功不一定发生能量的转化,故B错误;
C. 机械效率取决于有用功与总功的比值,与机械功率的大小无关,故C错误。
D. 一切具有做功本领的物体,是因为它具有能量,不能说它只具有机械能故D正确。
7.C
【详解】A.因为弹簧测力计的示数是2N,所以作用在绳端的拉力F为2N,故A错误。
B.由图可知,承担摩擦力的绳子股数是3,所以F=,f=6N。故B错误。
C.物体A在1s内内通过的距离:S′=vt=0.2m/s×1s=0.2m,绳子自由端移动的距离S=3S′=3×0.2m=0.6m,在1s内拉力F做功:
W=FS=2N×0.6m=1.2J.故C正确。
D.在1s内拉力F的功率:
P===1.2W,故D错误。
8.D
【详解】设一块砖的长度为L0,最上方的砖受两端的两砖的支持力作用而处于平衡,则砖对左方第二块砖压力
第二块砖在重力及压力的作用下而处于杠杆的平衡状态下,设露出部分长为x,则重心的位置离支点
;
则由杠杆的平衡条件可知:
;
则求得:
;
此图可知,此桥的最大跨度L为:
。
故选D。
9.B
【详解】踮脚时主要靠腓肠肌收缩,即动力由腓肠肌收缩产生,方向沿腓肠肌收缩的方向,竖直向上,
阻力为人的重力,双脚同时踮起时,每只脚上承担的重力为G′=G=×500N=250N;
踮一下脚尖时,脚绕O点转动,则O为支点,动力臂为MO,阻力臂为NO,
由杠杆的平衡条件:F1L1=F2L2,对每只脚来说:
F×MO=G′×NO,
即:F×2NO=250N×NO,
解得:F=125N。
故选:B。
10.A
【分析】被举高的物体具有重力势能,重力势能的大小与质量和被举高的高度有关,结合图中装置的特点可确定物体重心位置的变化。
【详解】由图可知,该模型轨道A端比B端高,且从B端到A端,轨道间间距增大,所以物体由C处自由释放,会向A端滚动,由于其重心降低,不计摩擦和空气阻力,滚动体质量不变,高度降低,所以重力势能减小,转化为滚动体的动能。
故选A。
11.B
【详解】
当力F顺时针方向转动过程中,力F的力臂L、L′、L″如图所示,
由图示可知,在旋转过程中,力臂先变大,后变小;在此过程中阻力与阻力臂不变,动力臂先增大,后减小,由杠杆平衡条件:动力×动力臂=阻力×阻力臂,可知:力F先减小,后变大,故ADC错误,B正确。
12.A
【详解】①物块C向右移动时,水平方向上受向右的推力,水平面向左的摩擦力和AB对C向左的摩擦力,因为物体间力的作用是相互的,所以C对木板AB的摩擦力是向右的,故①正确;
②木板AB在竖直方向上受重力和物块C对它的支持力的作用,在水平方向上受木块C对它向右的摩擦力,故②错误;
③物块C受到的重力、地面对它的支持力以及木板AB对它的压力,所以物块C受到的重力和地面对它的支持力不是一对平衡力,故③错误;
④以杆为研究对象,杆受重力G和C对它的支持力F支,两力臂如图所示:
根据杠杆平衡条件可得:F支 L支=G LG,
水平力F由A向B缓慢匀速推动木块,F支的力臂在减小,重力G及其力臂LG均不变,
所以根据杠杆平衡条件可知,在整个过程中支持力在逐渐增大;
由于支持力逐渐变大,且力的作用是相互的,所以可知杆对物体C的压力也逐渐变大,
根据影响摩擦力大小的因素可知,C和木板间、C和地面间的摩擦力逐渐增大,由力的平衡条件知,水平推力F也逐渐增大,故④正确。
综合分析只有①④正确。
故A符合题意。
13.等于 不变
【详解】[1]木箱受到推力向前做匀速直线运动,木箱处于平衡状态,受到的推力与摩擦力为一对平衡力,所以木箱受到的推力大小等于摩擦力大小;
[2]木箱沿水平地面运动运动,其质量、速度、高度都不变,所以其动能和重力势能不变,机械能不变。
14. = <
【详解】[1]斜面AB倾斜角度小于AC,所以物体沿AB运动时拉力较小,使用任何机械都不省功,所以拉力在两斜面上做功相同。
[2]速度相同,物体沿AC运动时用时较少,根据公式P=可知,物体沿AC运动时拉力做功的功率较大。
15. 静止 24
【详解】[1]由F t图象可知,第2秒末的推力F=2N,由v t图象可知,物体处于静止状态,则物体受到的摩擦力和推力是一对平衡力,二力大小相等,所以,物体受到的摩擦力为2N。
[2]由F t图象可知,6s 9s内的推力F′=4N,由v t图象可知,物体以v=2m/s的速度做匀速直线运动,处于平衡状态,此时物体受到的摩擦力为4N,由v=可得,第6秒末到第9秒末物体运动的距离
s=vt=2m/s×3s=6m
推力F做的功
W=F′s=4N×6m=24J
16.小于
【分析】根据杠杆的平衡条件和秤杆上密度的刻度变化进行判断.
【详解】提纽左侧为动力、动力臂;提纽右侧为阻力、阻力臂.根据杠杆的平衡条件得,因为动力臂不变,没有完全浸没酒精中,动力比完全浸没时变大,阻力不变,阻力臂变大,秤砣向右移动,测得值小于真实值.
17. mghA mghA 不处于 mg(hA hD)
【分析】(1)利用W=Gh求重力做功;
(2)根据机械能守恒定律判断小球在C点时具有能量大小;
(3)根据球在E位置的运动趋势判断受力情况;
(4)铁球对弹簧做功,不考虑能量的损失,铁球的能量全部转化为弹簧的能量。
【详解】(1)[1]从A位置到B位置的竖直高度为hA,所以铁球从A位置到B位置重力做功
W=GhA=mghA
(2)[2]铁球在A位置时,只有重力势能,则有
A点的机械能=A点重力势能=GhA=mghA
整个过程不计摩擦和能量损耗,故铁球机械能守恒,故有
在C点时小球具有的能量=在A点时小球具有的能量=GhA=mghA
(3)[3]小球达到E点时,虽然速度为0,但小球在水平方向只受弹簧的弹力作用,故小球不处于平衡状态。
(4)[4]铁球在E点只具有的重力势能,D、E在同一高度上,则有
E处铁球的重力势能=GhE=GhD
整个过程铁球
机械能的减少量=GhA GhD= G(hA hD)
根据能量守恒定律可知
弹簧的弹性势能增加量=铁球机械能的减少量= G(hA hD)=mg(hA hD)
18. 右 消除杠杆自身重力对平衡条件的影响,直接在杠杆上测出力臂
【详解】(1)[1][2]由图甲知,杠杆不在水平位置平衡,左端向下倾斜,则重心应向右移动,故应向右调节左端或右端的平衡螺母,使杠杆在水平位置平衡;其目的是使杠杆重心落在支点上,消除杠杆自身重力对平衡条件的影响,方便直接在杠杆上测出力臂。
(2)[3]把石块挂在杠杆右侧A处,钩码挂在杠杆左侧B处,使杠杆在水平位置平衡,如图乙所示,用刻度尺测量出OA的长l1和OB的长l,设钩码的重力为G,石块的质量为,石块的体积为,则
①
保持钩码及其位置B不变化,把石块全部浸没装有水的烧杯中;移动石块,直至使杠杆水平静止,即再次平衡,如图丙所示,测量出长l2,则
②
此时石块受重力,浮力和细线的拉力而平衡,排开水的体积等于石块的体积,由二力平衡条件得
代入②整理得
③
联立①③得
整理得石块密度的表达式为
19.(1)
(2)见解析
【详解】(1)l=Lcosθ
=Lcos60°
=
故力臂l为
(2)由杠杆平衡得:
FL1=GL2
解法1:FLcos=G1/2Lsin F=1/2Gtan当0<<900时,tan随着的增大而增大,所以F逐渐增大。
解法2:FL1=GL2 通过观察发现,随着的增大,L1减小而L2增大,因此L2/L1增大,而F=GL2/L1,所以,F逐渐增大。
20.(1)120N (2)60N (3)2m
【详解】(1) 小薇在A点时,杠杆平衡,杠杆受小薇对A点的压力和硬杆对C点的拉力,其中OA=1 m,OC=AB-OA-BC=5 m-1 m-1 m=3 m,根据杠杆的平衡条件可得GA所以F==120N,
(2) 小薇站在A点时,电流表的示数为0.1A,此时电路中的电阻R==30,由乙图可知F支=60N;
(3) 小薇在A点时,硬杆受到的力如解图①所示。
由力的平衡条件和前面数据可得,硬杆的重力G=F支+F拉=60 N+120 N=180 N。
当I′=0.3 A时,由I=可得,压敏电阻的阻值R′===10 Ω,由图乙知,当R=10 Ω时,地面对杆的支持力F支′=300 N。
由于F支′>G,所以可知此时杠杆对硬杆产生的是压力,如解图②所示。由力的平衡条件可得,杠杆对硬杆的压力F压=F支′-G=300 N-180 N=120 N,由于力的作用是相互的,则硬杆对杠杆的支持力FC=F压=120 N,设此时小薇到支点O的距离为L,根据杠杆的平衡条件可得FC·OC=G人·L,即120 N×3 m=360 N×L,解得L=1 m,所以小薇应在支点O的左侧1 m处,则此时小薇到A点的距离s=OA+L=1 m+1 m=2 m。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.如图所示,一根长为L的木棒的B端放在截面直径为D的圆柱体上,且木棒保持水平,用水平力F推木棒的A端,圆柱体在水平地面上向前滚动,设木棒与圆柱体、圆柱体与地面间均无滑动现象,当把木棒从图甲位置匀速推至图乙位置时,推力F做的功是( )
A.FL/2 B.F(L +πD) C.2FL D.F(2L +πD)
2.粗细均匀长L重G的木棒横卧在水平地面上,用力提起一端使木棒以另一端为支撑点慢慢竖立,此过程中做功至少是 ( )
A.2GL B.GL C.0.5GL D.不好判断
3.如图,同一小球在同一高度以相同速度向三个不同方向抛出(不计空气阻力和摩擦),设小球刚落地时的速度分别为v1、v2、v3,则( )
A.v1>v2>v3 B.v1<v2<v3
C.v1=v2=v3 D.无法确定
4.如图所示,某同学用重力为l0N的动滑轮匀速提升重力为50N的物体。不计摩擦,则该同学所用拉力F的可能值是( )
A.20N B.25N C.30N D.35N
5.如图所示,在这个装置中,如果拉力F等于4牛,则甲、乙两个弹簧测力计的读数分别为( )
A.8牛,l2牛 B.12牛,8牛
C.8牛,8牛 D.12牛,l2牛
6.下列说法正确的是( )
A.机械的功率越大,机械工作时做功越快
B.机械的功率越大,机械工作时能量转化越多
C.机械的功率越大,机械效率越高
D.一切具有做功本领的物体,是因为它具有机械能
7.质量是6kg的物体A放在水平桌面上,利用图所示的装置使物体以0.2m/s的速度做匀速直线运动,弹簧测力计始终保持水平,其示数为2N,不计绳子的伸长和滑轮组内部的摩擦,则( )
A.作用在绳端的拉力F为6N
B.水平桌面对物体a的摩擦力是2N
C.在1s内拉力F做功1.2J
D.拉力F的功率是0.4W
8.由五块相同砖块构成的桥,如图所示,若每块砖长度为30厘米,则此桥的最大跨度L为( )
A.20厘米 B.30厘米 C.40厘米 D.50厘米
9.人在踮脚时主要靠腓肠肌收缩,如图所示,若某人的重量
为500牛,MO=2N0,则双脚同时踮起时,每只脚的腓肠肌的作用力是( )
A.250牛 B.125牛 C.500牛 D.1000牛
10.如图,AB是一个略向左下倾斜的轨道,轨道由两根小木棒组成,两根小木棒在A端的距离大,B端的距离小。现将一个两头尖,中间大的由C处自由释放,则我们可以观察到的现象( )
A.滚动体向高处A端滚动
B.滚动体向低处B端滚动
C.滚动体停在C处不动
D.以上三种情况都有可能发生
11.如图所示杠杆提升重物G,力F顺时针方向转动,并使杠杆始终在图示位置平衡,则力F的大小将
A.逐渐变小 B.先变小,再变大
C.先变大,再变小 D.逐渐变大
12.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中( )
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确
B.只有②③正确
C.只有①②正确
D.只有③④正确
二、填空题
13.如图所示,用水平力推水平地面上的大木箱,并向前做匀速直线运动。这时,木箱受到的推力 摩擦力(填“大于”“等于”“小于”),大木箱的机械能 (填“增大”“不变”“减小”)。
14.如图所示,将同一物体分别沿光滑的斜面AB、AC以相同的速度从底部匀速拉到顶点A,已知AB>AC,如果拉力做的功分别为W1、W2,拉力做功的功率分别为P1、P2,则W1 W2,P1 P2
15.如图甲所示,水平地面上的一物体,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体速度v与时间t的关系如图乙所示。则第2秒末时,物体处于 状态,第6秒末到第9秒末,推力F做功是 焦耳。
16.如图所示是一个自制密度秤,其外形和杆秤差不多.装秤钩的地方吊着一个铁块,提纽位于B处,秤砣放在A处时,秤杆恰好水平平衡.把铁块浸没在待测密度的液体中时,移动秤砣便可直接在杆上读出液体的密度.当测量水的密度时,秤砣在C位置密度秤水平平衡,若测量酒精的密度时,铁块没有完全浸没,则测量值 真实值(填“大于”、“等于”、“小于”)
三、探究题
17.过山车是一种富有刺激性的娱乐工具,小侠同学制作了一个过山车模型,如图所示,他把质量为m的铁球放在A点,然后让它沿轨道滚下,轨道的右侧有一弹簧,铁球先后经过B、C、D点,并沿水平轨道到达E点,已知B点离台面高度为零,A、D点离台面的高度分别为hA、hB,则
(1)从A位置到B位置铁球的重力做功大小为
(2)C点小球具有的机械能大小为
(3)当到达E点时,弹簧最短,小球的速度变为零,小球 (选填“处于”“不处于”)平衡状态
(4)铁球从A运动到E的过程中,弹簧的弹性势能增加量为 (整个过程中不计摩擦及能量损耗)。
18.实验小组设计了一个利用刻度尺、细线、质量未知的钩码和杠杆测量石块密度的实验方案,如图所示。
(1)调节杠杆平衡。杠杆静止时如图甲所示,此时应向 调节杠杆的平衡螺母,使杠杆在水平位置平衡,其目的是: ;
(2)测量石块密度。
①把石块挂在杠杆右侧A处,在杠杆左侧B位置挂上钩码,使杠杆水平平衡,如图乙所示,用刻度尺测量出OA的长l1;
②保持钩码及位置B不动,把石块全部浸没装有水的烧杯中;移动石块位置,使杠杆水平静止,如图丙所示,测量出长l2;
③石块密度表达式:ρ石= 。(用测量的物理量符号和ρ水表示)
四、简答题
23.如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力 F 缓慢将木棒拉动到竖直方向夹角为θ 的位置(转轴处摩擦不计)。问:
(1)在答题纸上画出θ=60°时拉力F的力臂l,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?
并推导拉力F与角度θ的关系式。
24.为探究平衡木受力特点,喜爱体操的小薇设计了一个平衡木模型。整个装置如图甲所示AB可绕支点O无摩擦转动,C处固定一竖直硬杆,硬杆的底部安装了压敏电阻片R,R所在的电路放在了硬杆内(整个装置除硬杆以外,其他部分的重力均不计),且AB=5m,OA=BC=1m,电源电压恒为3V,硬杆底部R阻值随地面对它的支持力F变化的关系如图乙所示,整个装置放在水平地面上,AB始终处于水平平衡状态,当重360N的小薇站在A点时,电流表的示数为0.1A,求:
(1)小薇在A点时,C处受到硬杆的拉力;
(2)小薇在A点时,地面对硬杆底部R的支持力;
(3)当电流表的示数为0.3A时,小薇距A点多少米
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】力F做功可以看成:对木板做的功加上对球做的功:对木板做的功:位移s1等于木板的长度L,由W=Fs,得W1=FL;
再看对球做的功:木板和球、球和地面没有滑动摩擦,只有滚动摩擦,所以球的位移s2就等于球转动的圈数,球转动的圈数又等于木板的长度L;由于推动过程是匀速运动,所以木板和球的受力都是平衡的,木板的推力F等于球对木板的摩擦力,木板对球和球对木板的摩擦力是一对相互作用力,两力是相等的,所以球受到的力也为F;由W=Fs,得 W2=FL;所以F做得总功 W=W1+W2=2FL,故C正确。
2.C
【分析】既然是均匀的木棒,那重心就在木棒中点的地方,那么用力提起一端使木棒以另一端为支撑点慢慢竖立起来,木棒的重心从水平到垂直的距离h=L,然后利用W=Gh即可得出答案.
【详解】由于木棒质地均匀,那么木棒的重心位于木棒的中点处;木棒由水平到竖立的过程中,重心移动了h=L;那么要想提起这根木棒,至少要做的功为W=Gh=G L=0.5GL.
故选C.
3.C
【详解】小球从抛出到落地,发生了重力势能和动能的转化;在不计空气阻力和摩擦的条件下,转化过程中,机械能守恒,即机械能的总和不变。小球抛出时的机械能与小球落地时的机械能相等;而小球落地时的势能为零,故机械能大小就是动能大小,即动能相等所以速度相同。
故选C。
4.D
【详解】由题图可知:拉力F的方向不是竖直向上的,则力F的力臂将不再是动滑轮的直径,而是小于直径,如图所示:
根据杠杆的平衡条件得:
因为,所以:
即:
故D项符合题意、ABC项不符合题意。
故选D。
5.B
【详解】绳子静止,根据二力平衡,绳子两头的拉力是相等的,每根绳子的拉力都是4N;弹簧秤甲的拉力由三段绳子来承担,每根绳子的拉力大小都是4N,所以甲的读数是12N;弹簧秤乙的拉力由两段绳子来承担,每根绳子的拉力大小都是4N,所以乙的读数是8N.
6.A
【详解】A. 机械功率大表明机械做功快,故A正确。
B. 机械的功率越大,机械做功越快,使用机械做功不一定发生能量的转化,故B错误;
C. 机械效率取决于有用功与总功的比值,与机械功率的大小无关,故C错误。
D. 一切具有做功本领的物体,是因为它具有能量,不能说它只具有机械能故D正确。
7.C
【详解】A.因为弹簧测力计的示数是2N,所以作用在绳端的拉力F为2N,故A错误。
B.由图可知,承担摩擦力的绳子股数是3,所以F=,f=6N。故B错误。
C.物体A在1s内内通过的距离:S′=vt=0.2m/s×1s=0.2m,绳子自由端移动的距离S=3S′=3×0.2m=0.6m,在1s内拉力F做功:
W=FS=2N×0.6m=1.2J.故C正确。
D.在1s内拉力F的功率:
P===1.2W,故D错误。
8.D
【详解】设一块砖的长度为L0,最上方的砖受两端的两砖的支持力作用而处于平衡,则砖对左方第二块砖压力
第二块砖在重力及压力的作用下而处于杠杆的平衡状态下,设露出部分长为x,则重心的位置离支点
;
则由杠杆的平衡条件可知:
;
则求得:
;
此图可知,此桥的最大跨度L为:
。
故选D。
9.B
【详解】踮脚时主要靠腓肠肌收缩,即动力由腓肠肌收缩产生,方向沿腓肠肌收缩的方向,竖直向上,
阻力为人的重力,双脚同时踮起时,每只脚上承担的重力为G′=G=×500N=250N;
踮一下脚尖时,脚绕O点转动,则O为支点,动力臂为MO,阻力臂为NO,
由杠杆的平衡条件:F1L1=F2L2,对每只脚来说:
F×MO=G′×NO,
即:F×2NO=250N×NO,
解得:F=125N。
故选:B。
10.A
【分析】被举高的物体具有重力势能,重力势能的大小与质量和被举高的高度有关,结合图中装置的特点可确定物体重心位置的变化。
【详解】由图可知,该模型轨道A端比B端高,且从B端到A端,轨道间间距增大,所以物体由C处自由释放,会向A端滚动,由于其重心降低,不计摩擦和空气阻力,滚动体质量不变,高度降低,所以重力势能减小,转化为滚动体的动能。
故选A。
11.B
【详解】
当力F顺时针方向转动过程中,力F的力臂L、L′、L″如图所示,
由图示可知,在旋转过程中,力臂先变大,后变小;在此过程中阻力与阻力臂不变,动力臂先增大,后减小,由杠杆平衡条件:动力×动力臂=阻力×阻力臂,可知:力F先减小,后变大,故ADC错误,B正确。
12.A
【详解】①物块C向右移动时,水平方向上受向右的推力,水平面向左的摩擦力和AB对C向左的摩擦力,因为物体间力的作用是相互的,所以C对木板AB的摩擦力是向右的,故①正确;
②木板AB在竖直方向上受重力和物块C对它的支持力的作用,在水平方向上受木块C对它向右的摩擦力,故②错误;
③物块C受到的重力、地面对它的支持力以及木板AB对它的压力,所以物块C受到的重力和地面对它的支持力不是一对平衡力,故③错误;
④以杆为研究对象,杆受重力G和C对它的支持力F支,两力臂如图所示:
根据杠杆平衡条件可得:F支 L支=G LG,
水平力F由A向B缓慢匀速推动木块,F支的力臂在减小,重力G及其力臂LG均不变,
所以根据杠杆平衡条件可知,在整个过程中支持力在逐渐增大;
由于支持力逐渐变大,且力的作用是相互的,所以可知杆对物体C的压力也逐渐变大,
根据影响摩擦力大小的因素可知,C和木板间、C和地面间的摩擦力逐渐增大,由力的平衡条件知,水平推力F也逐渐增大,故④正确。
综合分析只有①④正确。
故A符合题意。
13.等于 不变
【详解】[1]木箱受到推力向前做匀速直线运动,木箱处于平衡状态,受到的推力与摩擦力为一对平衡力,所以木箱受到的推力大小等于摩擦力大小;
[2]木箱沿水平地面运动运动,其质量、速度、高度都不变,所以其动能和重力势能不变,机械能不变。
14. = <
【详解】[1]斜面AB倾斜角度小于AC,所以物体沿AB运动时拉力较小,使用任何机械都不省功,所以拉力在两斜面上做功相同。
[2]速度相同,物体沿AC运动时用时较少,根据公式P=可知,物体沿AC运动时拉力做功的功率较大。
15. 静止 24
【详解】[1]由F t图象可知,第2秒末的推力F=2N,由v t图象可知,物体处于静止状态,则物体受到的摩擦力和推力是一对平衡力,二力大小相等,所以,物体受到的摩擦力为2N。
[2]由F t图象可知,6s 9s内的推力F′=4N,由v t图象可知,物体以v=2m/s的速度做匀速直线运动,处于平衡状态,此时物体受到的摩擦力为4N,由v=可得,第6秒末到第9秒末物体运动的距离
s=vt=2m/s×3s=6m
推力F做的功
W=F′s=4N×6m=24J
16.小于
【分析】根据杠杆的平衡条件和秤杆上密度的刻度变化进行判断.
【详解】提纽左侧为动力、动力臂;提纽右侧为阻力、阻力臂.根据杠杆的平衡条件得,因为动力臂不变,没有完全浸没酒精中,动力比完全浸没时变大,阻力不变,阻力臂变大,秤砣向右移动,测得值小于真实值.
17. mghA mghA 不处于 mg(hA hD)
【分析】(1)利用W=Gh求重力做功;
(2)根据机械能守恒定律判断小球在C点时具有能量大小;
(3)根据球在E位置的运动趋势判断受力情况;
(4)铁球对弹簧做功,不考虑能量的损失,铁球的能量全部转化为弹簧的能量。
【详解】(1)[1]从A位置到B位置的竖直高度为hA,所以铁球从A位置到B位置重力做功
W=GhA=mghA
(2)[2]铁球在A位置时,只有重力势能,则有
A点的机械能=A点重力势能=GhA=mghA
整个过程不计摩擦和能量损耗,故铁球机械能守恒,故有
在C点时小球具有的能量=在A点时小球具有的能量=GhA=mghA
(3)[3]小球达到E点时,虽然速度为0,但小球在水平方向只受弹簧的弹力作用,故小球不处于平衡状态。
(4)[4]铁球在E点只具有的重力势能,D、E在同一高度上,则有
E处铁球的重力势能=GhE=GhD
整个过程铁球
机械能的减少量=GhA GhD= G(hA hD)
根据能量守恒定律可知
弹簧的弹性势能增加量=铁球机械能的减少量= G(hA hD)=mg(hA hD)
18. 右 消除杠杆自身重力对平衡条件的影响,直接在杠杆上测出力臂
【详解】(1)[1][2]由图甲知,杠杆不在水平位置平衡,左端向下倾斜,则重心应向右移动,故应向右调节左端或右端的平衡螺母,使杠杆在水平位置平衡;其目的是使杠杆重心落在支点上,消除杠杆自身重力对平衡条件的影响,方便直接在杠杆上测出力臂。
(2)[3]把石块挂在杠杆右侧A处,钩码挂在杠杆左侧B处,使杠杆在水平位置平衡,如图乙所示,用刻度尺测量出OA的长l1和OB的长l,设钩码的重力为G,石块的质量为,石块的体积为,则
①
保持钩码及其位置B不变化,把石块全部浸没装有水的烧杯中;移动石块,直至使杠杆水平静止,即再次平衡,如图丙所示,测量出长l2,则
②
此时石块受重力,浮力和细线的拉力而平衡,排开水的体积等于石块的体积,由二力平衡条件得
代入②整理得
③
联立①③得
整理得石块密度的表达式为
19.(1)
(2)见解析
【详解】(1)l=Lcosθ
=Lcos60°
=
故力臂l为
(2)由杠杆平衡得:
FL1=GL2
解法1:FLcos=G1/2Lsin F=1/2Gtan当0<<900时,tan随着的增大而增大,所以F逐渐增大。
解法2:FL1=GL2 通过观察发现,随着的增大,L1减小而L2增大,因此L2/L1增大,而F=GL2/L1,所以,F逐渐增大。
20.(1)120N (2)60N (3)2m
【详解】(1) 小薇在A点时,杠杆平衡,杠杆受小薇对A点的压力和硬杆对C点的拉力,其中OA=1 m,OC=AB-OA-BC=5 m-1 m-1 m=3 m,根据杠杆的平衡条件可得GA所以F==120N,
(2) 小薇站在A点时,电流表的示数为0.1A,此时电路中的电阻R==30,由乙图可知F支=60N;
(3) 小薇在A点时,硬杆受到的力如解图①所示。
由力的平衡条件和前面数据可得,硬杆的重力G=F支+F拉=60 N+120 N=180 N。
当I′=0.3 A时,由I=可得,压敏电阻的阻值R′===10 Ω,由图乙知,当R=10 Ω时,地面对杆的支持力F支′=300 N。
由于F支′>G,所以可知此时杠杆对硬杆产生的是压力,如解图②所示。由力的平衡条件可得,杠杆对硬杆的压力F压=F支′-G=300 N-180 N=120 N,由于力的作用是相互的,则硬杆对杠杆的支持力FC=F压=120 N,设此时小薇到支点O的距离为L,根据杠杆的平衡条件可得FC·OC=G人·L,即120 N×3 m=360 N×L,解得L=1 m,所以小薇应在支点O的左侧1 m处,则此时小薇到A点的距离s=OA+L=1 m+1 m=2 m。
答案第1页,共2页
答案第1页,共2页
