1.4 充分条件与必要条件(第二课时) 课件(共26张PPT)
文档属性
| 名称 | 1.4 充分条件与必要条件(第二课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 820.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 17:02:26 | ||
图片预览







文档简介
(共26张PPT)
第一章 集合与常用逻辑用语
1.4.2 充要条件
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
1.4.2 充要条件
知识回顾
下列“若p,则q”形式的命题中,p是q的充分条件吗?
(2)若m>2,则m>3;
(1)若x=-1,则x2=1;
p是q的必要条件吗?
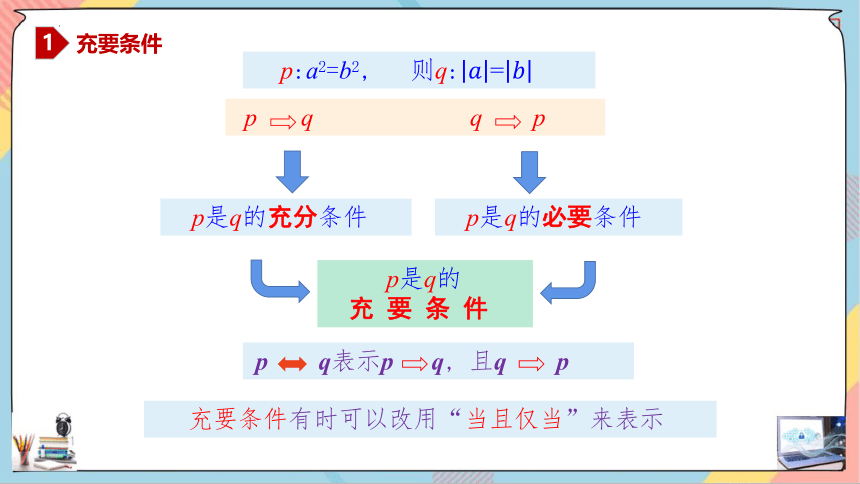
(3)若a2=b2,则=.
p:a2=b2, 则q:=
p q q p
充要条件
1
p是q的充分条件
p是q的必要条件
p是q的
充 要 条 件
p q表示p q, 且q p
充要条件有时可以改用“当且仅当”来表示
p与q的逻辑关系
2
思考
条件p与条件q之间有几种不同的逻辑关系?
①若p q ,且q p ,则p是q的充分不必要条件;
②若p q ,且q p ,则p是q的必要不充分条件;
④若p q ,且q p ,则p是q的充要条件.
③若p q ,且q p ,则p是q的即不充分也不必要条件;
练一练
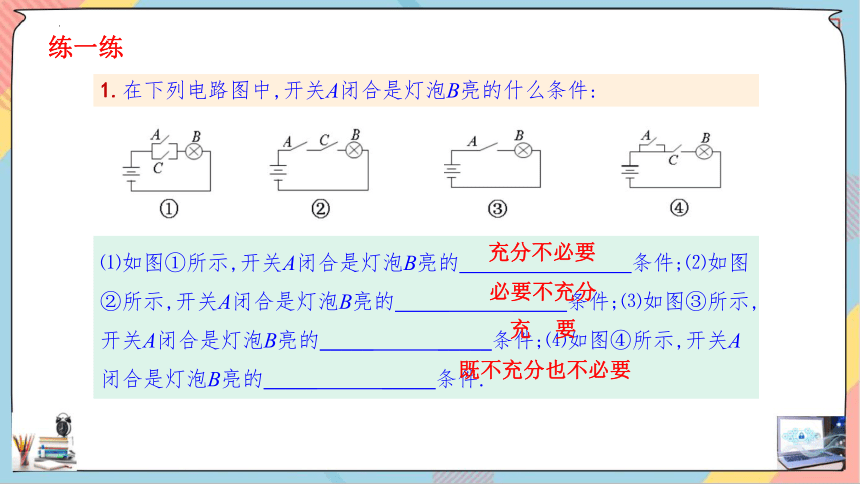
1.在下列电路图中,开关A闭合是灯泡B亮的什么条件:
⑴如图①所示,开关A闭合是灯泡B亮的_____ _____条件;⑵如图②所示,开关A闭合是灯泡B亮的_____ _____条件;⑶如图③所示,开关A闭合是灯泡B亮的_____ _____条件;⑷如图④所示,开关A闭合是灯泡B亮的_____ _____条件.
充分不必要
必要不充分
充 要
既不充分也不必要
1) p:同位角相等; q:两直线平行
2) p:两个角是对顶角; q:两个角相等
3) p:两个三角形周长相等; q:两个三角形面积相等
4) p:两个三棱锥底面积相等; q:两个三棱锥体积相等
2.下列各小题中,p是q的什么条件?
练一练
概括归
纳
已知 p:x∈A; q:x∈B
若A B,则p是q的充分不必要条件;
若B A,则p是q的必要不充分条件;
若A=B, 则p是q的充要条件;
若A B ,且B A, 则p是q的既不充分也不必要条件.
A
B
x
B
A
练一练
1.下列各小题中,p是q的什么条件?
(1) p:=2; q:x=3
(2) p:x∈A={x|1≤x≤3}; q:x∈B={x|-1≤x≤4}
(3) p:M∈{(x,y)|+≤1}; q:N∈{(x,y)|x2+y2≤1}
提示:
先将符号语言翻译成图形语言,再将图形语言对应成逻辑语言.
2.使不等式 |a|<3 成立的一个必要不充分条件是( )
A. a<3 B. |a|<2 C. a2<9 D. 0练一练
提示:
在数轴上,-3知识篇
素养篇
思维篇
1.4.2 充要条件
(一)充要条件的判断
示
例
方法
核心素养 之 数学建模 + 逻辑推理
分
析
充要条件判断的两个方面:(1)p q ? (2) q p ?
“a<0”是“ax2+1=0至少有一个负根”的( ).
A.充要条件 B.必要不充分条件
C.充分不必要 D.不充分不必要
一方面:a<0时,由ax2+1=0得, 有一个负根;
另一方面:由“ax2+1=0至少有一个负根”知,a=<0.
故选A.
对应练习:
若a, b∈R,则“a3>b3”是“a>b”成立的( )
A.充要条件 B.必要不充分条件
C.充分不必要 D.不充分不必要
(预备知识:a3-b3=(a-b)(a2+ab+b2))
示
例
方法
核心素养 之 数学建模 + 逻辑推理
分
析
充要条件证明方式一:(1)先证充分性; (2)再证必要性.
先证充分性:设原方程有两根x1,x2, x1<0再证必要性:由ac<0知 <0,又由韦达定理知x1x2=,
所以x1x2<0,即x1、x2一正一负.
求证:一元二次方程ax2+bx+c=0(a≠0)有一正根和一负根的充要条件是ac<0.
(二)充要条件的证明
对应练习:
若a, b∈R,求证:“a>b”是“a>b”的充要条件.
提示:
无论证充分性还是必要性,都要针对a,b的正负情况进行分类证明.
示
例
方法
核心素养 之 逻辑推理
分
析
充要条件证明方式二:对条件进行等价变形.
若a, b, x, y∈R,求证:的充要条件是.
注意
每一步的变形都必需是等价的!
表示“等价于”,即充要的意思
(二)充要条件的证明
对应练习:
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0
(预备知识:a3+b3=(a+b)(a2-ab+b2))
知识篇
素养篇
思维篇
1.4.2 充要条件
充要条件的应用
问
题
数学思想 之 函数与方程思想+数形结合
分
析
1.已知关于x的方程x2+6x+k=0有两个不相等的负实数根,
求参数k的取值范围.
从数的角度看:方程x2+6x+k=0有两个不相等的负实数根的充要条件是:判别式为正、两根之和为负且两根之积为正,易得0从形的角度看:函数y=x2+6x+k图像与x轴负半轴有两个交点,充要条件是:对称轴在y轴左侧,顶点在x轴下方,与y轴交点在x轴上方.可求得0方
法
等价变形的过程,可以是将自然语言翻译成符号语言,也可以是将自然语言翻译成图形语言,再翻译成符号语言.
对应练习:
求关于x的方程x2+(2m-1)x+m2=0有一个根大于1,另一个根小于1的充要条件.
提示:
数的角度:x1-1<0, 且x2-1>0(前提是判别式为正)
形的角度:函数y=x2+(2m-1)x+m2图像与x轴两个交点位于x=1异侧
充要条件的应用
问
题
数学思想 之 函数与方程思想+分类讨论
分
析
2.求关于x的方程m2x2-(m+1)x+2=0的所有根的和为2的充要
条件.
题目未明确是几次方程,故应分类讨论:
1)当m=0 时,x=2,符合题意;
2)当m≠0 时,充要条件是(m+1)2-8m2≥0且=2, 无解!
综上,所求充要条件为m=0.
方
法
1.系数含有参数的方程,要针对不同次数进行分类讨论;
2. 二次方程两根之和的前提是方程有根,即判别式非负!
课堂小结
一、本节课学习的新知识
充要条件的定义
充要条件的判断方法
充要条件的证明方法
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学建模
数学运算
三、本节课训练的数学思想方法
数形结合
转化与化归
函数与方程思想
课堂小结
分类讨论
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
给授课教师的建议:
1. 素养篇与思维篇中的问题,建议以学生分析为主,由
学生思考、探究、讨论,得出解决方案,教师适时点
拨即可;
2. 原PPT上的“分析”文本框内容,仅供教师参考,上
课前建议删除,使问题解决的过程得以原生态呈现.
(本页可以删了!)
第一章 集合与常用逻辑用语
1.4.2 充要条件
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
1.4.2 充要条件
知识回顾
下列“若p,则q”形式的命题中,p是q的充分条件吗?
(2)若m>2,则m>3;
(1)若x=-1,则x2=1;
p是q的必要条件吗?
(3)若a2=b2,则=.
p:a2=b2, 则q:=
p q q p
充要条件
1
p是q的充分条件
p是q的必要条件
p是q的
充 要 条 件
p q表示p q, 且q p
充要条件有时可以改用“当且仅当”来表示
p与q的逻辑关系
2
思考
条件p与条件q之间有几种不同的逻辑关系?
①若p q ,且q p ,则p是q的充分不必要条件;
②若p q ,且q p ,则p是q的必要不充分条件;
④若p q ,且q p ,则p是q的充要条件.
③若p q ,且q p ,则p是q的即不充分也不必要条件;
练一练
1.在下列电路图中,开关A闭合是灯泡B亮的什么条件:
⑴如图①所示,开关A闭合是灯泡B亮的_____ _____条件;⑵如图②所示,开关A闭合是灯泡B亮的_____ _____条件;⑶如图③所示,开关A闭合是灯泡B亮的_____ _____条件;⑷如图④所示,开关A闭合是灯泡B亮的_____ _____条件.
充分不必要
必要不充分
充 要
既不充分也不必要
1) p:同位角相等; q:两直线平行
2) p:两个角是对顶角; q:两个角相等
3) p:两个三角形周长相等; q:两个三角形面积相等
4) p:两个三棱锥底面积相等; q:两个三棱锥体积相等
2.下列各小题中,p是q的什么条件?
练一练
概括归
纳
已知 p:x∈A; q:x∈B
若A B,则p是q的充分不必要条件;
若B A,则p是q的必要不充分条件;
若A=B, 则p是q的充要条件;
若A B ,且B A, 则p是q的既不充分也不必要条件.
A
B
x
B
A
练一练
1.下列各小题中,p是q的什么条件?
(1) p:=2; q:x=3
(2) p:x∈A={x|1≤x≤3}; q:x∈B={x|-1≤x≤4}
(3) p:M∈{(x,y)|+≤1}; q:N∈{(x,y)|x2+y2≤1}
提示:
先将符号语言翻译成图形语言,再将图形语言对应成逻辑语言.
2.使不等式 |a|<3 成立的一个必要不充分条件是( )
A. a<3 B. |a|<2 C. a2<9 D. 0
提示:
在数轴上,-3
素养篇
思维篇
1.4.2 充要条件
(一)充要条件的判断
示
例
方法
核心素养 之 数学建模 + 逻辑推理
分
析
充要条件判断的两个方面:(1)p q ? (2) q p ?
“a<0”是“ax2+1=0至少有一个负根”的( ).
A.充要条件 B.必要不充分条件
C.充分不必要 D.不充分不必要
一方面:a<0时,由ax2+1=0得, 有一个负根;
另一方面:由“ax2+1=0至少有一个负根”知,a=<0.
故选A.
对应练习:
若a, b∈R,则“a3>b3”是“a>b”成立的( )
A.充要条件 B.必要不充分条件
C.充分不必要 D.不充分不必要
(预备知识:a3-b3=(a-b)(a2+ab+b2))
示
例
方法
核心素养 之 数学建模 + 逻辑推理
分
析
充要条件证明方式一:(1)先证充分性; (2)再证必要性.
先证充分性:设原方程有两根x1,x2, x1<0
所以x1x2<0,即x1、x2一正一负.
求证:一元二次方程ax2+bx+c=0(a≠0)有一正根和一负根的充要条件是ac<0.
(二)充要条件的证明
对应练习:
若a, b∈R,求证:“a>b”是“a>b”的充要条件.
提示:
无论证充分性还是必要性,都要针对a,b的正负情况进行分类证明.
示
例
方法
核心素养 之 逻辑推理
分
析
充要条件证明方式二:对条件进行等价变形.
若a, b, x, y∈R,求证:的充要条件是.
注意
每一步的变形都必需是等价的!
表示“等价于”,即充要的意思
(二)充要条件的证明
对应练习:
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0
(预备知识:a3+b3=(a+b)(a2-ab+b2))
知识篇
素养篇
思维篇
1.4.2 充要条件
充要条件的应用
问
题
数学思想 之 函数与方程思想+数形结合
分
析
1.已知关于x的方程x2+6x+k=0有两个不相等的负实数根,
求参数k的取值范围.
从数的角度看:方程x2+6x+k=0有两个不相等的负实数根的充要条件是:判别式为正、两根之和为负且两根之积为正,易得0
法
等价变形的过程,可以是将自然语言翻译成符号语言,也可以是将自然语言翻译成图形语言,再翻译成符号语言.
对应练习:
求关于x的方程x2+(2m-1)x+m2=0有一个根大于1,另一个根小于1的充要条件.
提示:
数的角度:x1-1<0, 且x2-1>0(前提是判别式为正)
形的角度:函数y=x2+(2m-1)x+m2图像与x轴两个交点位于x=1异侧
充要条件的应用
问
题
数学思想 之 函数与方程思想+分类讨论
分
析
2.求关于x的方程m2x2-(m+1)x+2=0的所有根的和为2的充要
条件.
题目未明确是几次方程,故应分类讨论:
1)当m=0 时,x=2,符合题意;
2)当m≠0 时,充要条件是(m+1)2-8m2≥0且=2, 无解!
综上,所求充要条件为m=0.
方
法
1.系数含有参数的方程,要针对不同次数进行分类讨论;
2. 二次方程两根之和的前提是方程有根,即判别式非负!
课堂小结
一、本节课学习的新知识
充要条件的定义
充要条件的判断方法
充要条件的证明方法
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学建模
数学运算
三、本节课训练的数学思想方法
数形结合
转化与化归
函数与方程思想
课堂小结
分类讨论
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
给授课教师的建议:
1. 素养篇与思维篇中的问题,建议以学生分析为主,由
学生思考、探究、讨论,得出解决方案,教师适时点
拨即可;
2. 原PPT上的“分析”文本框内容,仅供教师参考,上
课前建议删除,使问题解决的过程得以原生态呈现.
(本页可以删了!)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
