2.1 等式性质与不等式性质(第一课时) 课件(共32张PPT)
文档属性
| 名称 | 2.1 等式性质与不等式性质(第一课时) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 17:03:05 | ||
图片预览








文档简介
(共32张PPT)
第二章 一元二次函数、方程、不等式
2.1.1 不等关系与比较大小
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
2.1.1 不等关系与比较大小
在现实世界和日常生活中,存在着大量相等关系和不等关系.
例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过或不少于等.
现实世界的相等和不等关系
长短
轻重
高矮
大小
三个臭皮匠,顶个诸葛亮
语言文字里的相等和不等关系
人类的语言文字对相等和不等关系也有各种描述.
雷声大,雨点小
捡了芝麻,丢了西瓜
道高一尺,魔高一丈
欲穷千里目,更上一层楼
七上八下
半斤八两
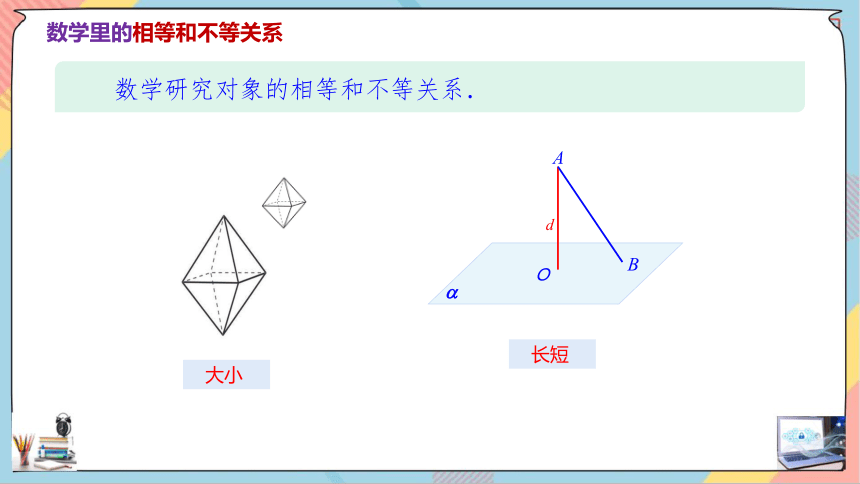
数学里的相等和不等关系
大小
数学研究对象的相等和不等关系.
A
B
d
O
长短
请用数学符号语言翻译以下交通限制标志信息:
v≤40 km/h
用数学研究相等和不等关系
1
m≤10 t
h≤3.5 m
8:00≤t≤20:00
1.某品牌酸奶的质量检查规定,酸奶中脂肪的含量f 应不少于2.5% ,蛋白质的含量p应不少于2.3%,
写成不等式组为 .
2.购买一批“六一”儿童节礼品,买笔记本每本18元,买钢笔每支25元,现有礼品预算300元,设笔记本买x本,钢笔买y支,则礼品数满足的关系式是 .
18x+25y≤300
f ≥2.5%
p ≥2.3%
数
学
抽
象
用数学研究相等和不等关系
1
数
学
抽
象
用数学研究相等和不等关系
1
3.某杂志以每本2.5元的价格发行时,发行量为8万册.经过调查,若价格每提高0.1元,发行量就减少2000册.如何定价才能使提价后的销售总收入不低于20万元?
若杂志的定价为x元,则销售总收入为(8-×0.2)x万元.
于是,不等关系 “销售总收入不低于20万元”可以用不等式表示为: (8-×0.2)x≥20
(要知道如何定价,还得解该不等式)
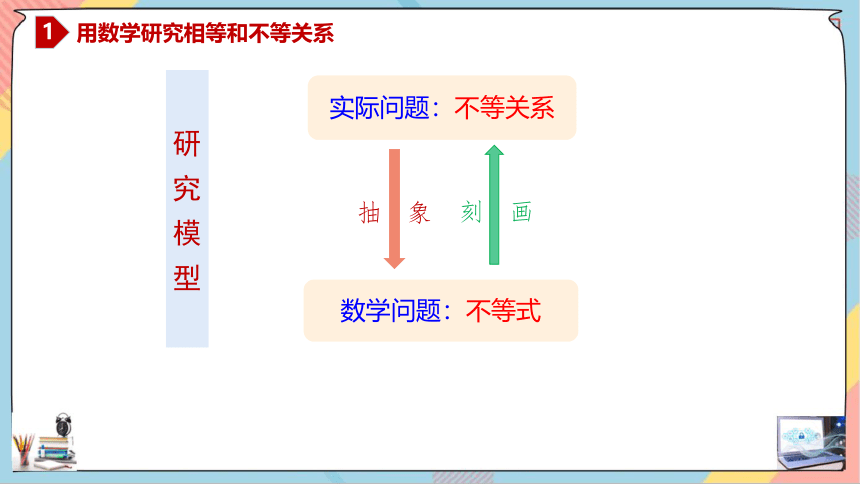
实际问题:不等关系
数学问题:不等式
抽 象
刻 画
用数学研究相等和不等关系
1
研究模型
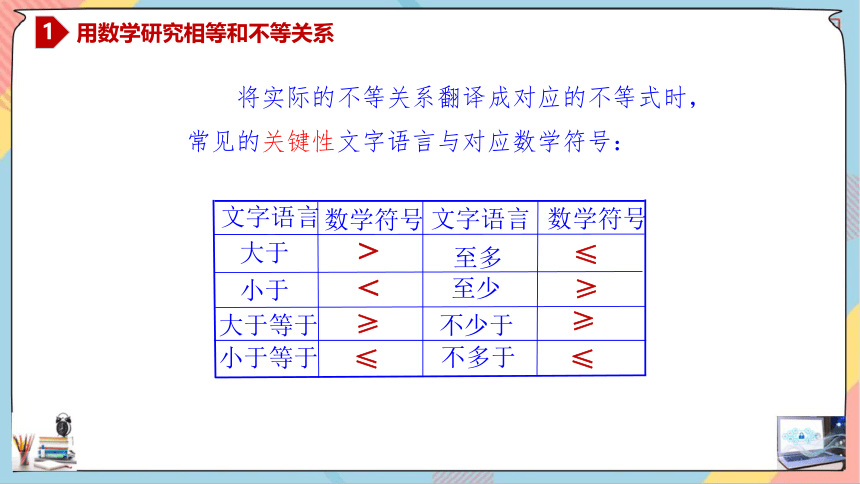
将实际的不等关系翻译成对应的不等式时,常见的关键性文字语言与对应数学符号:
文字语言
大于
小于
大于等于
小于等于
数学符号
>
<
≥
≤
文字语言
至多
至少
不少于
不多于
≤
数学符号
≥
≥
≤
用数学研究相等和不等关系
1
7 ℃≤t≤13 ℃
练一练
(1)今天的天气预报说:明天早晨的最低温度为7℃,明天白
天的最高温度为13℃.
(2)汽车站检票口有规定:儿童身高达到或超过120厘米的,
要买半票.
写出满足下列条件的不等式:
如果a-b是正数,那么a>b;
如果a-b等于零,那么a=b;
如果a-b是负数,那么a反过来也对.
两个实数比大小
2
要研究量与量之间的相等或不等关系,首先要解决的是两个实数之间比大小.
b
a
aa
b
a>b
两个实数比大小
2
例题:比较(a+3)(a-5)与(a+2)(a-4)的大小.
∵(a+3)(a-5)-(a+2)(a-4)
=(a2-2a-15)-(a2-2a-8)
=-7
∴(a+3)(a-5)-(a+2)(a-4)<0
∴(a+3)(a-5)<(a+2)(a-4)
解:
作差
变形
定符号
定大小
作差比较法
已知a>b,求证:a> .
练一练
知识篇
素养篇
思维篇
2.1.1 不等关系与比较大小
方
法
总结
核心素养 之 数学运算 + 逻辑推理
1. 比较下列各题中两数之间的大小:
(1)x2+y2+3x+3y 与 x-y-6 (x,y∈R)
(2)- 与
(3) 与 (x∈R)
问
题
(1)∵ (x2+y2+3x-3y ) - (x- y-6)
= x2+y2+2x+4y +6
= (x+1)2+(y+2)2+1 > 0
∴ x2+y2+3x+3y > x-y-6
作差之后为多项式结构,常用分组因式分解或分组配方来确定正负.
解
答
方
法总结
核心素养 之 数据分析 + 逻辑推理
问
题
(2)∵(- =
=<0
∴ <
作差之后的变形环节,用到了分子有理化和通分的化归技巧;对于根式的差,分子有理化是常用的变形技术.
解
答
1. 比较下列各题中两数之间的大小:
(1)x2+y2+3x+3y 与 x-y-6 (x,y∈R)
(2)- 与
(3) 与 (x∈R)
核心素养 之 数学运算 + 逻辑推理
(3)∵ -
=≤0
∴ 当x=1时,= ;当x≠1时,
方
法总结
问
题
解
答
作差之后通分,接着分子部分配方. 利用完全平方的非负性确定正负号;由于有相等的可能,故结论分开交待.
1. 比较下列各题中两数之间的大小:
(1)x2+y2+3x+3y 与 x-y-6 (x,y∈R)
(2)- 与
(3) 与 (x∈R)
核心素养 之 数学抽象 + 数学建模
数
学
抽
象
过
程
正方形内含四个全等的直角三角形(中间留一小正方形空档)
图形语言:
S大正方形>4S直角三角形
a2+b2≥2ab (a=b时取等号)
符号化
量化
逻辑推理
?
符号语言:
数学模型:
论证模型:
设直角三角形的两条直角
边的长为a,b (a≠b)
核心素养 之 逻辑推理
问
题
求证: a2+b2≥2ab (当a=b时取等号)
证明:∵ a2+b2-2ab
=(a-b)2 ≥0
∴ a2+b2≥2ab (当a=b时取等号)
论
证
方法总结
不等式就是用不等号连结两个数(式)得到的式子;
故证明不等式,本质上就是比较两个数的大小. 这里用了作差比较法,今后会学习别的证明方法.
核心素养 之 数学抽象 + 数学建模
数
学
抽
象
过
程
为什么糖水中加的糖越多越甜?
生活问题:
a克糖水中含有b(a>b>0)克糖,再加入m(m>0)克糖,糖水更甜了,为什么?
> (a>b>0,m>0)
(定性描述)
(定量描述)
量化
符号化
逻辑推理
?
数学问题:
数学模型:
论证模型:
核心素养 之 逻辑推理
问
题
求证: > (a>b>0,m>0)
证明:∵ -
=
=>0
∴
论
证
方法总结
对于两个分数(式)比大小,作差后往往通分,对分子部分进行分组因式分解.
知识篇
素养篇
思维篇
2.1.1 不等关系与比较大小
数学思想 之 主元思想 + 配方法
1. 比较 a2-2ab+2b2 与2a-3 (a , b∈R)的大小.
问
题
解法一:∵( a2-2ab+2b2 )-(2a-3 )
=a2-2(b+1)a+2b2+3
=[a2-2(b+1)a+(b+1)2]+b2-2b+2
=[a-(b+1) ]2+(b-1 )2+1>0
∴ a2-2ab+2b2 >2a-3
方法总结
第一部分以a为主元配方,其余部分以b为主元配方,利用完全平方的非负性定正负符号.
解
答
1. 比较 a2-2ab+2b2 与2a-3 (a , b∈R)的大小.
问
题
解法二:∵( a2-2ab+2b2)-(2a-3 )
= (2b2-2ab)+a2-2a+3
=2(b-)2+-2a+3
=2(b-)2+(a-2 )2+1>0
∴ a2-2ab+2b2 >2a-3
方法总结
第一部分以b为主元配方,其余部分以a为主元配方,利用完全平方的非负性定正负符号.
解
答
数学思想 之 主元思想 + 配方法
数学思想 之 函数思想 + 方程思想
1. 比较 a2-2ab+2b2 与2a-3 (a , b∈R)的大小.
问
题
解法三:( a2-2ab+2b2 )-(2a-3 )
=a2-2(b+1)a+2b2+3 ①
视①式为变量a的二次函数. 其判别式为
△=4(b+1)2-8b2-12=-4b2+8b-8
=-4(b-1)2-4 < 0
∴a2-2(b+1)a+2b2+3 >0恒成立,
∴ a2-2ab+2b2 >2a-3
方法总结
作差后,以函数的眼光看待①式,并利用一元二次方程判别式的正负来判断①式的正负.
解
答
数学思想 之 分类讨论
2. 比较 a-1 与 (a∈R)的大小.
问
题
解:( a-1 )-= =
0
-1
2
当a<-1或0当-12时,( a-1 )- ,( a-1 )>
当a=-1 或a =2时,( a-1 )- ,( a-1 )=
判断多个因式的积或商的正负,往往辅助以数轴,用序轴标根确定各部分的正负.
解
答
方法总结
数学思想 之 转化与化归
问
题
3. 求证: > (a>b>0,m>0)
证明:∵a>b>0,m>0
∴ =
=1+ >1
∴
解
答
对于两个同号的数比大小,还可以考虑作商比较.
方法总结
已知a >0, b>0:
1 a>b ; 1 ; 1 a课堂小结
一、本节课学习的新知识
相等与不等关系
从问题中抽象出不等式
比较两个数的大小
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学运算
三、本节课训练的数学思想方法
函数结合
转化与化归
方程思想
课堂小结
分类讨论
主元思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
第二章 一元二次函数、方程、不等式
2.1.1 不等关系与比较大小
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
2.1.1 不等关系与比较大小
在现实世界和日常生活中,存在着大量相等关系和不等关系.
例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过或不少于等.
现实世界的相等和不等关系
长短
轻重
高矮
大小
三个臭皮匠,顶个诸葛亮
语言文字里的相等和不等关系
人类的语言文字对相等和不等关系也有各种描述.
雷声大,雨点小
捡了芝麻,丢了西瓜
道高一尺,魔高一丈
欲穷千里目,更上一层楼
七上八下
半斤八两
数学里的相等和不等关系
大小
数学研究对象的相等和不等关系.
A
B
d
O
长短
请用数学符号语言翻译以下交通限制标志信息:
v≤40 km/h
用数学研究相等和不等关系
1
m≤10 t
h≤3.5 m
8:00≤t≤20:00
1.某品牌酸奶的质量检查规定,酸奶中脂肪的含量f 应不少于2.5% ,蛋白质的含量p应不少于2.3%,
写成不等式组为 .
2.购买一批“六一”儿童节礼品,买笔记本每本18元,买钢笔每支25元,现有礼品预算300元,设笔记本买x本,钢笔买y支,则礼品数满足的关系式是 .
18x+25y≤300
f ≥2.5%
p ≥2.3%
数
学
抽
象
用数学研究相等和不等关系
1
数
学
抽
象
用数学研究相等和不等关系
1
3.某杂志以每本2.5元的价格发行时,发行量为8万册.经过调查,若价格每提高0.1元,发行量就减少2000册.如何定价才能使提价后的销售总收入不低于20万元?
若杂志的定价为x元,则销售总收入为(8-×0.2)x万元.
于是,不等关系 “销售总收入不低于20万元”可以用不等式表示为: (8-×0.2)x≥20
(要知道如何定价,还得解该不等式)
实际问题:不等关系
数学问题:不等式
抽 象
刻 画
用数学研究相等和不等关系
1
研究模型
将实际的不等关系翻译成对应的不等式时,常见的关键性文字语言与对应数学符号:
文字语言
大于
小于
大于等于
小于等于
数学符号
>
<
≥
≤
文字语言
至多
至少
不少于
不多于
≤
数学符号
≥
≥
≤
用数学研究相等和不等关系
1
7 ℃≤t≤13 ℃
练一练
(1)今天的天气预报说:明天早晨的最低温度为7℃,明天白
天的最高温度为13℃.
(2)汽车站检票口有规定:儿童身高达到或超过120厘米的,
要买半票.
写出满足下列条件的不等式:
如果a-b是正数,那么a>b;
如果a-b等于零,那么a=b;
如果a-b是负数,那么a
两个实数比大小
2
要研究量与量之间的相等或不等关系,首先要解决的是两个实数之间比大小.
b
a
a
b
a>b
两个实数比大小
2
例题:比较(a+3)(a-5)与(a+2)(a-4)的大小.
∵(a+3)(a-5)-(a+2)(a-4)
=(a2-2a-15)-(a2-2a-8)
=-7
∴(a+3)(a-5)-(a+2)(a-4)<0
∴(a+3)(a-5)<(a+2)(a-4)
解:
作差
变形
定符号
定大小
作差比较法
已知a>b,求证:a> .
练一练
知识篇
素养篇
思维篇
2.1.1 不等关系与比较大小
方
法
总结
核心素养 之 数学运算 + 逻辑推理
1. 比较下列各题中两数之间的大小:
(1)x2+y2+3x+3y 与 x-y-6 (x,y∈R)
(2)- 与
(3) 与 (x∈R)
问
题
(1)∵ (x2+y2+3x-3y ) - (x- y-6)
= x2+y2+2x+4y +6
= (x+1)2+(y+2)2+1 > 0
∴ x2+y2+3x+3y > x-y-6
作差之后为多项式结构,常用分组因式分解或分组配方来确定正负.
解
答
方
法总结
核心素养 之 数据分析 + 逻辑推理
问
题
(2)∵(- =
=<0
∴ <
作差之后的变形环节,用到了分子有理化和通分的化归技巧;对于根式的差,分子有理化是常用的变形技术.
解
答
1. 比较下列各题中两数之间的大小:
(1)x2+y2+3x+3y 与 x-y-6 (x,y∈R)
(2)- 与
(3) 与 (x∈R)
核心素养 之 数学运算 + 逻辑推理
(3)∵ -
=≤0
∴ 当x=1时,= ;当x≠1时,
方
法总结
问
题
解
答
作差之后通分,接着分子部分配方. 利用完全平方的非负性确定正负号;由于有相等的可能,故结论分开交待.
1. 比较下列各题中两数之间的大小:
(1)x2+y2+3x+3y 与 x-y-6 (x,y∈R)
(2)- 与
(3) 与 (x∈R)
核心素养 之 数学抽象 + 数学建模
数
学
抽
象
过
程
正方形内含四个全等的直角三角形(中间留一小正方形空档)
图形语言:
S大正方形>4S直角三角形
a2+b2≥2ab (a=b时取等号)
符号化
量化
逻辑推理
?
符号语言:
数学模型:
论证模型:
设直角三角形的两条直角
边的长为a,b (a≠b)
核心素养 之 逻辑推理
问
题
求证: a2+b2≥2ab (当a=b时取等号)
证明:∵ a2+b2-2ab
=(a-b)2 ≥0
∴ a2+b2≥2ab (当a=b时取等号)
论
证
方法总结
不等式就是用不等号连结两个数(式)得到的式子;
故证明不等式,本质上就是比较两个数的大小. 这里用了作差比较法,今后会学习别的证明方法.
核心素养 之 数学抽象 + 数学建模
数
学
抽
象
过
程
为什么糖水中加的糖越多越甜?
生活问题:
a克糖水中含有b(a>b>0)克糖,再加入m(m>0)克糖,糖水更甜了,为什么?
> (a>b>0,m>0)
(定性描述)
(定量描述)
量化
符号化
逻辑推理
?
数学问题:
数学模型:
论证模型:
核心素养 之 逻辑推理
问
题
求证: > (a>b>0,m>0)
证明:∵ -
=
=>0
∴
论
证
方法总结
对于两个分数(式)比大小,作差后往往通分,对分子部分进行分组因式分解.
知识篇
素养篇
思维篇
2.1.1 不等关系与比较大小
数学思想 之 主元思想 + 配方法
1. 比较 a2-2ab+2b2 与2a-3 (a , b∈R)的大小.
问
题
解法一:∵( a2-2ab+2b2 )-(2a-3 )
=a2-2(b+1)a+2b2+3
=[a2-2(b+1)a+(b+1)2]+b2-2b+2
=[a-(b+1) ]2+(b-1 )2+1>0
∴ a2-2ab+2b2 >2a-3
方法总结
第一部分以a为主元配方,其余部分以b为主元配方,利用完全平方的非负性定正负符号.
解
答
1. 比较 a2-2ab+2b2 与2a-3 (a , b∈R)的大小.
问
题
解法二:∵( a2-2ab+2b2)-(2a-3 )
= (2b2-2ab)+a2-2a+3
=2(b-)2+-2a+3
=2(b-)2+(a-2 )2+1>0
∴ a2-2ab+2b2 >2a-3
方法总结
第一部分以b为主元配方,其余部分以a为主元配方,利用完全平方的非负性定正负符号.
解
答
数学思想 之 主元思想 + 配方法
数学思想 之 函数思想 + 方程思想
1. 比较 a2-2ab+2b2 与2a-3 (a , b∈R)的大小.
问
题
解法三:( a2-2ab+2b2 )-(2a-3 )
=a2-2(b+1)a+2b2+3 ①
视①式为变量a的二次函数. 其判别式为
△=4(b+1)2-8b2-12=-4b2+8b-8
=-4(b-1)2-4 < 0
∴a2-2(b+1)a+2b2+3 >0恒成立,
∴ a2-2ab+2b2 >2a-3
方法总结
作差后,以函数的眼光看待①式,并利用一元二次方程判别式的正负来判断①式的正负.
解
答
数学思想 之 分类讨论
2. 比较 a-1 与 (a∈R)的大小.
问
题
解:( a-1 )-= =
0
-1
2
当a<-1或0
当a=-1 或a =2时,( a-1 )- ,( a-1 )=
判断多个因式的积或商的正负,往往辅助以数轴,用序轴标根确定各部分的正负.
解
答
方法总结
数学思想 之 转化与化归
问
题
3. 求证: > (a>b>0,m>0)
证明:∵a>b>0,m>0
∴ =
=1+ >1
∴
解
答
对于两个同号的数比大小,还可以考虑作商比较.
方法总结
已知a >0, b>0:
1 a>b ; 1 ; 1 a
一、本节课学习的新知识
相等与不等关系
从问题中抽象出不等式
比较两个数的大小
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学运算
三、本节课训练的数学思想方法
函数结合
转化与化归
方程思想
课堂小结
分类讨论
主元思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
