人教版数学八年级上册 11.2.1 三角形的内角教案
文档属性
| 名称 | 人教版数学八年级上册 11.2.1 三角形的内角教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 95.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 20:10:07 | ||
图片预览

文档简介
11.2.1 三角形的内角
教学目标:
1、通过操作活动探索发现和验证“三角形的内角和是180度”的规律。
2、使学生在观察、操作、分析、猜想、验证、合作、交流等具体活动中,提高动手操作能力、数学思考能力及数学推理能力,并运用新知识解决问题。
3.让学生在探究数学的过程中体验发现的乐趣,增强学好数学的信心,体验数学学习成功的喜悦。
教学重点:
探究发现和验证“三角形的内角和180度”这一规律的过程,并归纳总结出规律。
教学难点:
对不同探究方法的指导和学生对规律的灵活应用。
教具学具准备:
多媒体课件、学生准备三角形纸片,量角器、三角板。
教学过程:
1、知识回顾
师:同学们,在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.
学生讨论发言,教师总结。
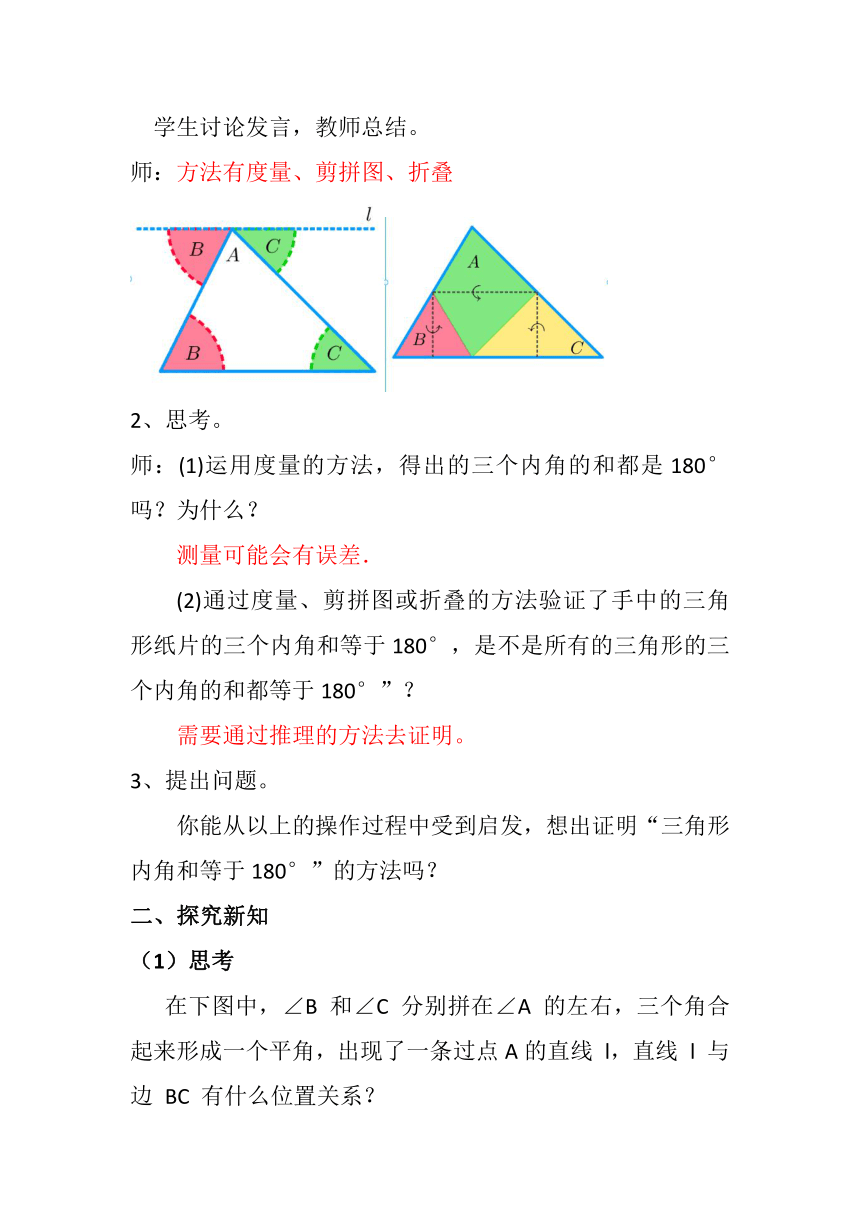
师:方法有度量、剪拼图、折叠
2、思考。
师:(1)运用度量的方法,得出的三个内角的和都是180° 吗?为什么?
测量可能会有误差.
(2)通过度量、剪拼图或折叠的方法验证了手中的三角 形纸片的三个内角和等于180°,是不是所有的三角形的三个内角的和都等于180°”?
需要通过推理的方法去证明。
3、提出问题。
你能从以上的操作过程中受到启发,想出证明“三角形内角和等于180°”的方法吗?
二、探究新知
(1)思考
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A的直线 l,直线 l 与边 BC 有什么位置关系?
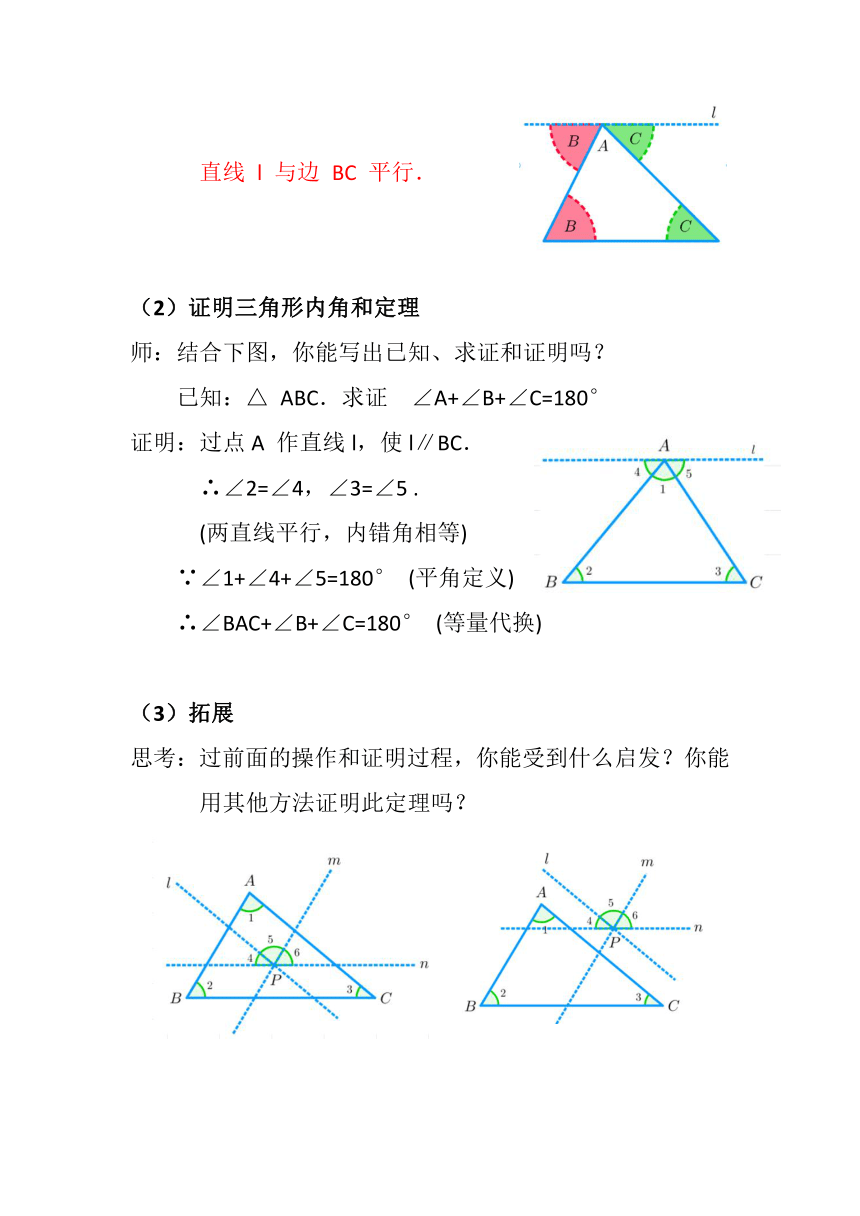
直线 l 与边 BC 平行.
(2)证明三角形内角和定理
师:结合下图,你能写出已知、求证和证明吗?
已知:△ ABC .求证∠A+∠B+∠C=180°
证明:过点A 作直线l,使l∥BC.
∴∠2=∠4,∠3=∠5 .
(两直线平行,内错角相等)
∵∠1+∠4+∠5=180° (平角定义)
∴∠BAC+∠B+∠C=180° (等量代换)
(3)拓展
思考:过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?
(4)总结
三角形内角和定理:三角形内角和为 180°。
师:为了证明的需要,在原来的图形上添加的线叫做辅助线。 在平面几何里,辅助线通常画成虚线。
思路:为了证明三个角的和为180°通常转化为一个平角或两平行线间的同旁内角.这种转化思想是数学中的常用方法.
(5)三角形内角和定理的辨析
例题1:判断下列说法对吗?
①钝角三角形的内角和大于锐角三角形的内角和. ( )
②在直角三角形中,两个锐角的和等于90 . ( )
③在钝角三角形中,两个锐角的和大于90 . ( )
④三角形中有一个角是60 ,那么这个三角形一定是个
锐角三角形. ( )
⑤一个三角形中一定不可能有两个钝角. ( )
例题2:若一个三角形三个内角度数的比为 2︰3︰4,那么这个三角形是( )
A .直角三角形 B .锐角三角形
C .钝角三角形 D .等边三角形
例题3:(1)一个三角形中最多有 1 个直角。
(2) 一个三角形中最多有 1 个钝角。
(3)一个三角形中至少有 2 个锐角。
(4)任意 一个三角形中,最大的一个角的度数至少为 60°。
拓展训练1
小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来一个角,另一块有原来两个角。他想重新买一块玻璃安上,小明非常聪明,只带了其中一块去玻璃店去,就配到了和原来一模一样的玻璃。你知道他带的哪一块吗?
拓展训练2
直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.
在 △ ABC 中∠C=90°,则 ∠ A+∠ B=90°。
推论:直角三角形的两个锐角互余。
反之,有两个角互余的三角形是直角三角形。
三、课堂练习
1、看图,求未知角的度数。
2、书上88页10题。
教师:刚才,我们利用了三角形的什么?
3、求出下面三角形各角的度数。
(1)我三边相等。
(2)我是等腰三角形,我的顶角是96°。
(3)我是直角三角形,有一个锐角是40°。
四、课堂小结。
师:这节课你有什么收获?
五、板书设计:
三角形的内角和
三角形内角和定理:三角形内角和为 180°。
为了证明的需要,在原来的图形上添加的线叫做辅助线。 在平面几何里,辅助线通常画成虚线。
推论:直角三角形的两个锐角互余。
反之,有两个角互余的三角形是直角三角形。
6、教学反思
本课设计思路,让学生经历了观察、发现、猜测、验证、归纳、概括等数学活动,切实体现了新课程的核心理念“以学生为本,以学生的发展为本”,在验证三角形内角和是180度的过程中,教师要有意识地引导学生把三角形的内角和转化成了平角,使学生对“转化”的数学思想有所感悟;在对测量的结果出现不同答案的交流过程中,使学生认识到测量时会出现误差,从而培养学生严谨的、科学的学习态度和探究精神。促使学生人人动手、人人思考,引导学生在独立思考的基础上进行合作与交流。使学生在动手“做”数学的过程中寻求成功,在成功中享受快乐,在快乐中不断超越,在超越中体验成长.
教学目标:
1、通过操作活动探索发现和验证“三角形的内角和是180度”的规律。
2、使学生在观察、操作、分析、猜想、验证、合作、交流等具体活动中,提高动手操作能力、数学思考能力及数学推理能力,并运用新知识解决问题。
3.让学生在探究数学的过程中体验发现的乐趣,增强学好数学的信心,体验数学学习成功的喜悦。
教学重点:
探究发现和验证“三角形的内角和180度”这一规律的过程,并归纳总结出规律。
教学难点:
对不同探究方法的指导和学生对规律的灵活应用。
教具学具准备:
多媒体课件、学生准备三角形纸片,量角器、三角板。
教学过程:
1、知识回顾
师:同学们,在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.
学生讨论发言,教师总结。
师:方法有度量、剪拼图、折叠
2、思考。
师:(1)运用度量的方法,得出的三个内角的和都是180° 吗?为什么?
测量可能会有误差.
(2)通过度量、剪拼图或折叠的方法验证了手中的三角 形纸片的三个内角和等于180°,是不是所有的三角形的三个内角的和都等于180°”?
需要通过推理的方法去证明。
3、提出问题。
你能从以上的操作过程中受到启发,想出证明“三角形内角和等于180°”的方法吗?
二、探究新知
(1)思考
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A的直线 l,直线 l 与边 BC 有什么位置关系?
直线 l 与边 BC 平行.
(2)证明三角形内角和定理
师:结合下图,你能写出已知、求证和证明吗?
已知:△ ABC .求证∠A+∠B+∠C=180°
证明:过点A 作直线l,使l∥BC.
∴∠2=∠4,∠3=∠5 .
(两直线平行,内错角相等)
∵∠1+∠4+∠5=180° (平角定义)
∴∠BAC+∠B+∠C=180° (等量代换)
(3)拓展
思考:过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?
(4)总结
三角形内角和定理:三角形内角和为 180°。
师:为了证明的需要,在原来的图形上添加的线叫做辅助线。 在平面几何里,辅助线通常画成虚线。
思路:为了证明三个角的和为180°通常转化为一个平角或两平行线间的同旁内角.这种转化思想是数学中的常用方法.
(5)三角形内角和定理的辨析
例题1:判断下列说法对吗?
①钝角三角形的内角和大于锐角三角形的内角和. ( )
②在直角三角形中,两个锐角的和等于90 . ( )
③在钝角三角形中,两个锐角的和大于90 . ( )
④三角形中有一个角是60 ,那么这个三角形一定是个
锐角三角形. ( )
⑤一个三角形中一定不可能有两个钝角. ( )
例题2:若一个三角形三个内角度数的比为 2︰3︰4,那么这个三角形是( )
A .直角三角形 B .锐角三角形
C .钝角三角形 D .等边三角形
例题3:(1)一个三角形中最多有 1 个直角。
(2) 一个三角形中最多有 1 个钝角。
(3)一个三角形中至少有 2 个锐角。
(4)任意 一个三角形中,最大的一个角的度数至少为 60°。
拓展训练1
小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来一个角,另一块有原来两个角。他想重新买一块玻璃安上,小明非常聪明,只带了其中一块去玻璃店去,就配到了和原来一模一样的玻璃。你知道他带的哪一块吗?
拓展训练2
直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.
在 △ ABC 中∠C=90°,则 ∠ A+∠ B=90°。
推论:直角三角形的两个锐角互余。
反之,有两个角互余的三角形是直角三角形。
三、课堂练习
1、看图,求未知角的度数。
2、书上88页10题。
教师:刚才,我们利用了三角形的什么?
3、求出下面三角形各角的度数。
(1)我三边相等。
(2)我是等腰三角形,我的顶角是96°。
(3)我是直角三角形,有一个锐角是40°。
四、课堂小结。
师:这节课你有什么收获?
五、板书设计:
三角形的内角和
三角形内角和定理:三角形内角和为 180°。
为了证明的需要,在原来的图形上添加的线叫做辅助线。 在平面几何里,辅助线通常画成虚线。
推论:直角三角形的两个锐角互余。
反之,有两个角互余的三角形是直角三角形。
6、教学反思
本课设计思路,让学生经历了观察、发现、猜测、验证、归纳、概括等数学活动,切实体现了新课程的核心理念“以学生为本,以学生的发展为本”,在验证三角形内角和是180度的过程中,教师要有意识地引导学生把三角形的内角和转化成了平角,使学生对“转化”的数学思想有所感悟;在对测量的结果出现不同答案的交流过程中,使学生认识到测量时会出现误差,从而培养学生严谨的、科学的学习态度和探究精神。促使学生人人动手、人人思考,引导学生在独立思考的基础上进行合作与交流。使学生在动手“做”数学的过程中寻求成功,在成功中享受快乐,在快乐中不断超越,在超越中体验成长.
