23.1 第一课时旋转的概念与性质 课件(共21张PPT) 2023-2024学年九年级数学上册人教版
文档属性
| 名称 | 23.1 第一课时旋转的概念与性质 课件(共21张PPT) 2023-2024学年九年级数学上册人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 960.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 20:23:08 | ||
图片预览




文档简介
(共21张PPT)
第1课时 旋转的概念与性质
第二十三章 旋转
23.1 图形的旋转
教学目标
掌握旋转的有关概念及基本性质.
能够根据旋转的基本性质解决实际问题.
1
2
指针式钟表的指针在不停地转动,风车风轮的每个
叶片在风的吹动下转动到新的位置.这些现象有哪些共
同特点?
新课导入
1.旋转是图形变化的方法之一,应该怎样描述它呢?
方向?度数?
2.旋转又有什么性质呢?
全等?
新课导入
新知探究
知识点一:旋转的概念
B
O
A
45
0
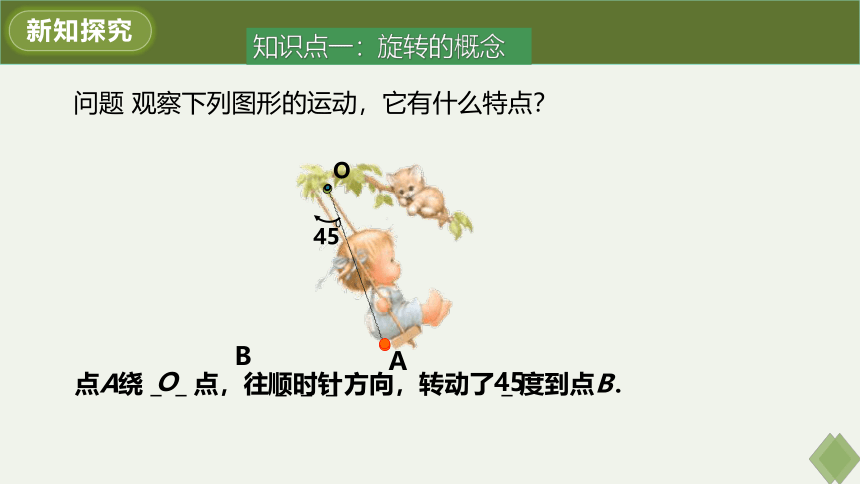
问题 观察下列图形的运动,它有什么特点?
点A绕__点,往___方向,转动了_度到点B.
O
顺时针
45
钟表的指针在不停地转动,从12时到4时,时针转动了______度.
120°
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
思考:怎样来定义这种图形变换?
知识点一:旋转的概念
新知探究
知识点一:旋转的概念
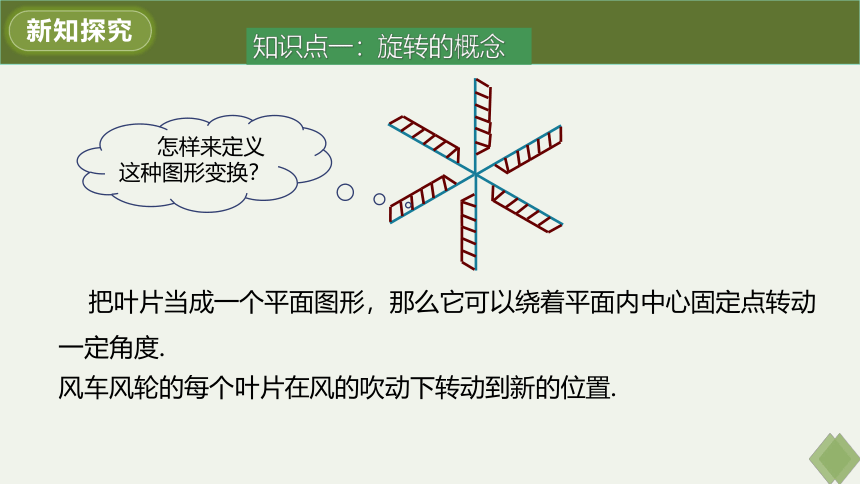
风车风轮的每个叶片在风的吹动下转动到新的位置.
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
新知探究
知识点一:旋转的概念
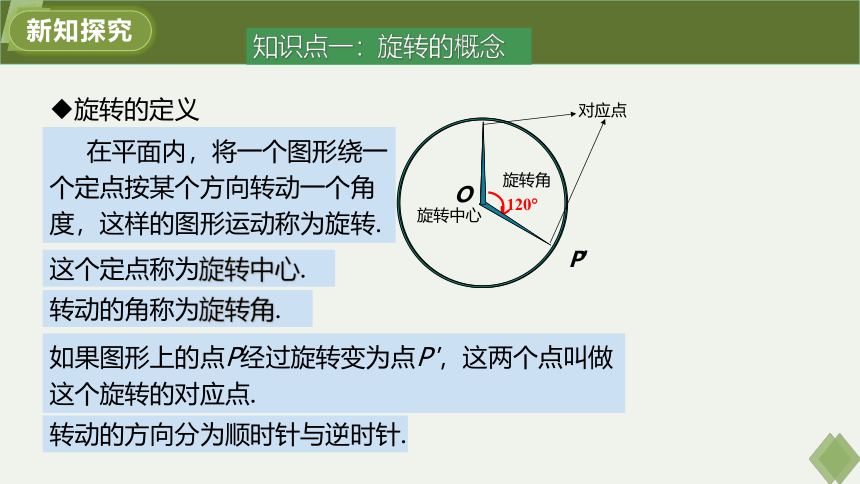
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
O
P′
旋转中心
旋转角
对应点
旋转的定义
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
新知探究
知识点一:旋转的概念
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
温馨提示:(1)旋转的范围是“平面内”,其中“旋转中心,
旋转方向,旋转角度”称之为旋转的三要素;
(2)旋转变换同样属于全等变换.
新知探究
如图,△DEF是由△ ABC旋转所得点A,
线段AB,∠A分别转到了什么位置?
D
A
DE
AB
∠D
∠A
对应点
对应边
对应角
旋转中心是:
旋转的方向是:
旋转角是:
点O
逆时针
∠AOD
∠BOE
∠COF
知识点二:旋转的性质
新知探究
知识点二:旋转的性质
(3)旋转前、后的图形全等.
(1)对应点到旋转中心的距离相等.
(2)对应点与旋转中心所连线段的夹角等于旋转角.
(3)△ABC ≌△A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
(1)OA=OA′,
B
A
B
A
C
C
OB=OB′,
OC=OC′.
O
归纳小结
练习1. 如图,△ADE绕点D的顺时针旋转,旋转的角是∠ADE,得到△CDB,那么下列说法错误的是( ).
A.DE平分∠ADB B.AD=DC
C.AE∥BD D.AE=BC
C
巩固练习
想一想 如图,将△ABC 逆时针旋转得到△DEF,如何确定它们的旋转中心位置?
D
E
B
F
C
A
如图,两组对应点所连线段的垂直平分线的交点 O,即为旋转中心.
O
知识点三:确定旋转中心位置
巩固练习
旋转中心的确定:
根据旋转的性质可知,对应点到旋转中心的距离相等,所以旋转中心位于对应点连线的垂直平分线上,即旋转中心是两对对应点所连线段的垂直平分线的交点。
归纳小结
1.时钟的时针在不停地转动,从上午 6 时到上午 9
时,时针旋转的旋转角是多少度?从上午 9 时到上午 10
时呢?
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转
中心在哪里?旋转角是哪个角?
课堂练习
3.如图所示,△AOB绕着点O顺时针旋转至△A′OB′的位置,此时:
(1)点B的对应点是______;
(2)旋转中心是________,旋转角为________________;
(3)∠A的对应角是______,线段OB的对应线段是________.
点B'
点O
∠AOA'或∠BOB'
∠A'
OB'
课堂练习
4. △A′OB′是△AOB绕点O按逆时针方向旋转得到的.已知∠AOB=20°, ∠A′OB =24°,AB=3,OA=5,则∠A′OA = ,OA ′ = ,旋转角等于 °.
3
44 °
44
课堂练习
5.如图,A,B,C三点共线,△ACD和△BCE都是等边三角形,△ACE旋转后到达△DCB的位置.
(1) 旋转中心是哪一点
(2) 旋转角是多少度
(1)C点,只有C点是不动的点。
(2)60°。 ACD的边AC转到 ACD的边CD,旋转角为∠ACD,为60°
课堂练习
6.如图,在△AOB中,AB⊥OB,∠A=30° ,OA=4 ,将△OAB绕点O旋转150°得△OA'B',则点A'的坐标为 .
课堂练习
旋转
旋转三要素
旋转的定义
旋转的性质
旋转的相关概念
旋转中心、旋转方向、旋转角
旋转中心
旋转角
对应点
课堂总结
23.1 图形的旋转
第一课时旋转的概念与性质
谢谢观看
旋转
第1课时 旋转的概念与性质
第二十三章 旋转
23.1 图形的旋转
教学目标
掌握旋转的有关概念及基本性质.
能够根据旋转的基本性质解决实际问题.
1
2
指针式钟表的指针在不停地转动,风车风轮的每个
叶片在风的吹动下转动到新的位置.这些现象有哪些共
同特点?
新课导入
1.旋转是图形变化的方法之一,应该怎样描述它呢?
方向?度数?
2.旋转又有什么性质呢?
全等?
新课导入
新知探究
知识点一:旋转的概念
B
O
A
45
0
问题 观察下列图形的运动,它有什么特点?
点A绕__点,往___方向,转动了_度到点B.
O
顺时针
45
钟表的指针在不停地转动,从12时到4时,时针转动了______度.
120°
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
思考:怎样来定义这种图形变换?
知识点一:旋转的概念
新知探究
知识点一:旋转的概念
风车风轮的每个叶片在风的吹动下转动到新的位置.
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
新知探究
知识点一:旋转的概念
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
O
P′
旋转中心
旋转角
对应点
旋转的定义
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
新知探究
知识点一:旋转的概念
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
温馨提示:(1)旋转的范围是“平面内”,其中“旋转中心,
旋转方向,旋转角度”称之为旋转的三要素;
(2)旋转变换同样属于全等变换.
新知探究
如图,△DEF是由△ ABC旋转所得点A,
线段AB,∠A分别转到了什么位置?
D
A
DE
AB
∠D
∠A
对应点
对应边
对应角
旋转中心是:
旋转的方向是:
旋转角是:
点O
逆时针
∠AOD
∠BOE
∠COF
知识点二:旋转的性质
新知探究
知识点二:旋转的性质
(3)旋转前、后的图形全等.
(1)对应点到旋转中心的距离相等.
(2)对应点与旋转中心所连线段的夹角等于旋转角.
(3)△ABC ≌△A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
(1)OA=OA′,
B
A
B
A
C
C
OB=OB′,
OC=OC′.
O
归纳小结
练习1. 如图,△ADE绕点D的顺时针旋转,旋转的角是∠ADE,得到△CDB,那么下列说法错误的是( ).
A.DE平分∠ADB B.AD=DC
C.AE∥BD D.AE=BC
C
巩固练习
想一想 如图,将△ABC 逆时针旋转得到△DEF,如何确定它们的旋转中心位置?
D
E
B
F
C
A
如图,两组对应点所连线段的垂直平分线的交点 O,即为旋转中心.
O
知识点三:确定旋转中心位置
巩固练习
旋转中心的确定:
根据旋转的性质可知,对应点到旋转中心的距离相等,所以旋转中心位于对应点连线的垂直平分线上,即旋转中心是两对对应点所连线段的垂直平分线的交点。
归纳小结
1.时钟的时针在不停地转动,从上午 6 时到上午 9
时,时针旋转的旋转角是多少度?从上午 9 时到上午 10
时呢?
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转
中心在哪里?旋转角是哪个角?
课堂练习
3.如图所示,△AOB绕着点O顺时针旋转至△A′OB′的位置,此时:
(1)点B的对应点是______;
(2)旋转中心是________,旋转角为________________;
(3)∠A的对应角是______,线段OB的对应线段是________.
点B'
点O
∠AOA'或∠BOB'
∠A'
OB'
课堂练习
4. △A′OB′是△AOB绕点O按逆时针方向旋转得到的.已知∠AOB=20°, ∠A′OB =24°,AB=3,OA=5,则∠A′OA = ,OA ′ = ,旋转角等于 °.
3
44 °
44
课堂练习
5.如图,A,B,C三点共线,△ACD和△BCE都是等边三角形,△ACE旋转后到达△DCB的位置.
(1) 旋转中心是哪一点
(2) 旋转角是多少度
(1)C点,只有C点是不动的点。
(2)60°。 ACD的边AC转到 ACD的边CD,旋转角为∠ACD,为60°
课堂练习
6.如图,在△AOB中,AB⊥OB,∠A=30° ,OA=4 ,将△OAB绕点O旋转150°得△OA'B',则点A'的坐标为 .
课堂练习
旋转
旋转三要素
旋转的定义
旋转的性质
旋转的相关概念
旋转中心、旋转方向、旋转角
旋转中心
旋转角
对应点
课堂总结
23.1 图形的旋转
第一课时旋转的概念与性质
谢谢观看
旋转
同课章节目录
