2.1 等式性质与不等式性质(第二课时) 课件(共26张PPT)
文档属性
| 名称 | 2.1 等式性质与不等式性质(第二课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第二章 一元二次函数、方程、不等式
2.1.2 不等式的性质
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
2.1.2 不等式的性质
上一课时我们学习了比较两个数的大小,为我们学习不等式的性质奠定了基础. 让我们先回顾等式的有关性质:
性质1 如果a=b,那么b=a;
性质2 如果a=b,b=c,那么a=c;
性质3 如果a=b,那么a±c=b±c;
性质4 如果a=b,那么ac=bc;
性质5 如果a=b,c≠0,那么=.
等式有下面的基本性质:
接下来,我们类比等式的性质,猜想不等式的性质,请你给出证明.
不等式的性质:
性质1 如果a>b,那么b性质2 如果a>b,b>c,那么a>c;(传递性)
不等式的性质
1
不等式的性质:
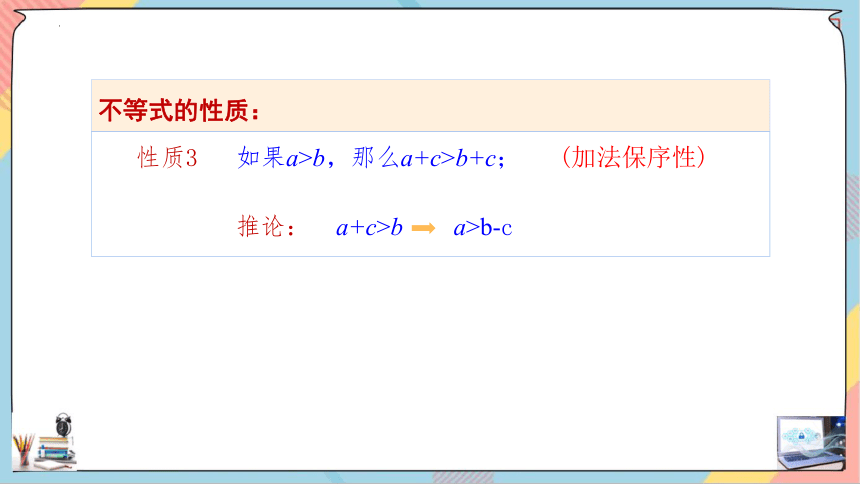
性质3 如果a>b,那么a+c>b+c; (加法保序性)
推论: a+c>b a>b-c
证明:ac-bc=(a-b)c
∵ a>b, ∴a-b>0
∴ c>0时, ac-bc>0, ac>bc;
c<0时, ac-bc<0, ac不等式的性质:
性质4 如果a>b,c>0,那么ac>bc ;(正数保序性)
如果a>b,c<0,那么ac<bc . (负数反序性)
不等式的性质:
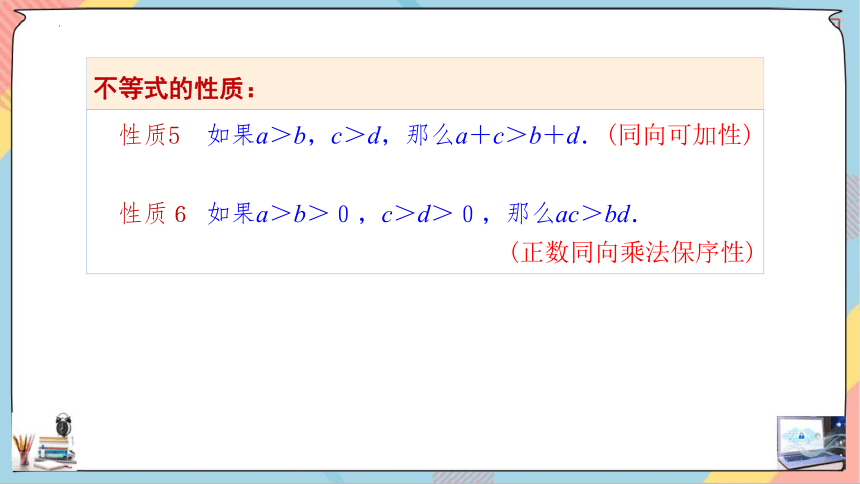
性质5 如果a>b,c>d,那么a+c>b+d.(同向可加性)
性质6 如果a>b>0,c>d>0,那么ac>bd.
(正数同向乘法保序性)
特别地:若a>b>0,则
> (保序性)
0< < (反序性)
不等式的性质:
性质7 如果a>b>0,那么an>bn (n∈N,n≥2)
(正数乘方保序性)
性质8 如果a>b>0,那么> (n∈N,n≥2)
(正数开方保序性)
(1)如果a>b,c<d,那么a-c b-d;
(2)如果a>b>0,c<d<0,那么ac bd;
(3)如果a>b>0,那么 ;
(4)如果a>b>c>0,那么
练一练
1. 用不等号 “>”或 “<”填空:
答案: (1)>; (2)>; (3)<; (4)<.
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
练一练
2. 已知x,y∈R,则“|x|+|y|>0”是“x>0”的 ( )
答案: B
2
不等式性质的应用
例题.已知a>b>0, c<0, > .
证明: 因为a>b>0, 所以ab>0, >0
所以a× > b× ;
即 > ;
又c<0, 所以 .
正数同向可乘性
倒数保号性
正数保序性
负数反序性
A.x2<ax<a2 B.x2>ax>a2
C.x2<a2<ax D.x2>a2>ax
答案:B
练一练
设x<a<0,则下列不等式一定成立的是( )
知识篇
素养篇
思维篇
2.1.2 不等式的性质
1.对于实数a,b,c, 给出下列命题:
①若a>b,则ac2>bc2; ②若aab>b2;
③若a>b,则a2>b2; ④若a
其中,正确命题的序号是 .
方
法
总结
核心素养 之 逻辑推理 + 数据分析
问
题
解
答
填②④ ①不严密! c=0时不成立;
②因为-a>-b>0,所以(-a)(-a)>(-a)(-b)>(-b)(-b)
③换一种叙述:若a>b,a>b ,则aa>bb; 错误!
④因为-a>-b>0,所以>>0, 所以 (-a)()>(-b))
不等式的推导过程,每一步都必需有依据,而主要依据就是实数大小的事实和不等式的性质.
2.(1)设a,b∈R,若a->0,则下列不等式中正确的是( )
A. b-a>0 B. a3+b3<0 C. a2-b2<0 D. a+b>0
方
法
总结
核心素养 之 逻辑推理 + 数据分析
问
题
解
答
(1)选D 注意到≥-b
(2)选D 因为-c>-d >0,所以>>0, 所以 a()>b()>0
在不等式推导过程中,常用到的两个结论:
1) ≥±x 2) a>b>0时,>>0
(2)若a>b>0,cA.> B.< C.> D. <
3.已知12方
法
总结
核心素养 之 逻辑推理 + 数据分析
问
题
解
答
因为15又12即-24不等式中出现减法运算时,要调整为加上减数的相反数,再用不等式的同向可加性;
两个正数的倒数具有反序性.
知识篇
素养篇
思维篇
2.1.2 不等式的性质
1.设a>0, 不等式-c < ax+b < c的解集是{x|-2则a:b:c= .
数学思想 之 转化与化归
问
题
解
答
方法总结
由-c < ax+b < c得-b-c c-b
又因为a>0, 所以
由已知,有, =1
解得:=,= , 所以a:b:c=2 : 1: 3
解不等式过程中的每一步化归,都用到不等式的性质;运用不等式的性质时,要检查性质的前提条件.
数学思想 之 转化与化归
问
题
解
答
2.已知a,b,c∈R,a+b+c=0, abc<0,求证:>0.
证明:由a+b+c=0,abc<0知 a,b,c中两正一负;
不妨设a>0,b>0, c<0 ; 则
===
因为 -c=a+b>0 ,所以 c2=(a+b)2>ab
所以 -c2+ab<0, 又abc<0 , 所以
方法
对于轮换式,可以作出具体的假设,以利于进一步推导.
3.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且
三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分
别为x,y,z,且x分别为a,b,c,且a元)是( )
A.ax+by+cz B.az+by+cx C.ay+bz+cx D.ay+bx+cz
数学思想 之 极端思想
问
题
解
答
选B
根据极端思想,用粉刷费用最低的涂料粉刷面积最大的房间,且用粉刷费用最高的涂料粉刷面积最小的房间,这样所需总费用最低,最低总费用为(az+by+cx)元.
可以用作差比较法加以验证.
注意:根据正数同向可乘性能得到的是最高的总费用;另一种极端情况就能得到最低的总费用.
方法总结
4.已知-2数学思想 之 转化与化归
问
题
解
答
设m=a+b, n=a-b, 则-2所以-6<3m≤15, -8≤-2n≤2;
又a+5b=3m-2n,所以-14已知二元不等式,可以通过换元转化为一元不等式;目标式的转化可以用观察法或待定系数法.
方法总结
5.若-10数学思想 之 分类讨论
问
题
解
答
1)当a≥0时,+b=a+b;
由0≤a<8, 02)当a<0时,+b=-a+b;
由0<-a<10, -10又由a综合1),2) 得:0<+b<18
1.目标式带有绝对值的,要分类讨论;
2 .两个变量取值有关联时,要注意其对目标式的影响.
方法总结
课堂小结
一、本节课学习的新知识
不等式的性质
不等式性质的应用
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学运算
三、本节课训练的数学思想方法
转化与化归
课堂小结
分类讨论
极端思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
第二章 一元二次函数、方程、不等式
2.1.2 不等式的性质
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
2.1.2 不等式的性质
上一课时我们学习了比较两个数的大小,为我们学习不等式的性质奠定了基础. 让我们先回顾等式的有关性质:
性质1 如果a=b,那么b=a;
性质2 如果a=b,b=c,那么a=c;
性质3 如果a=b,那么a±c=b±c;
性质4 如果a=b,那么ac=bc;
性质5 如果a=b,c≠0,那么=.
等式有下面的基本性质:
接下来,我们类比等式的性质,猜想不等式的性质,请你给出证明.
不等式的性质:
性质1 如果a>b,那么b
不等式的性质
1
不等式的性质:
性质3 如果a>b,那么a+c>b+c; (加法保序性)
推论: a+c>b a>b-c
证明:ac-bc=(a-b)c
∵ a>b, ∴a-b>0
∴ c>0时, ac-bc>0, ac>bc;
c<0时, ac-bc<0, ac
性质4 如果a>b,c>0,那么ac>bc ;(正数保序性)
如果a>b,c<0,那么ac<bc . (负数反序性)
不等式的性质:
性质5 如果a>b,c>d,那么a+c>b+d.(同向可加性)
性质6 如果a>b>0,c>d>0,那么ac>bd.
(正数同向乘法保序性)
特别地:若a>b>0,则
> (保序性)
0< < (反序性)
不等式的性质:
性质7 如果a>b>0,那么an>bn (n∈N,n≥2)
(正数乘方保序性)
性质8 如果a>b>0,那么> (n∈N,n≥2)
(正数开方保序性)
(1)如果a>b,c<d,那么a-c b-d;
(2)如果a>b>0,c<d<0,那么ac bd;
(3)如果a>b>0,那么 ;
(4)如果a>b>c>0,那么
练一练
1. 用不等号 “>”或 “<”填空:
答案: (1)>; (2)>; (3)<; (4)<.
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
练一练
2. 已知x,y∈R,则“|x|+|y|>0”是“x>0”的 ( )
答案: B
2
不等式性质的应用
例题.已知a>b>0, c<0, > .
证明: 因为a>b>0, 所以ab>0, >0
所以a× > b× ;
即 > ;
又c<0, 所以 .
正数同向可乘性
倒数保号性
正数保序性
负数反序性
A.x2<ax<a2 B.x2>ax>a2
C.x2<a2<ax D.x2>a2>ax
答案:B
练一练
设x<a<0,则下列不等式一定成立的是( )
知识篇
素养篇
思维篇
2.1.2 不等式的性质
1.对于实数a,b,c, 给出下列命题:
①若a>b,则ac2>bc2; ②若a
③若a>b,则a2>b2; ④若a
其中,正确命题的序号是 .
方
法
总结
核心素养 之 逻辑推理 + 数据分析
问
题
解
答
填②④ ①不严密! c=0时不成立;
②因为-a>-b>0,所以(-a)(-a)>(-a)(-b)>(-b)(-b)
③换一种叙述:若a>b,a>b ,则aa>bb; 错误!
④因为-a>-b>0,所以>>0, 所以 (-a)()>(-b))
不等式的推导过程,每一步都必需有依据,而主要依据就是实数大小的事实和不等式的性质.
2.(1)设a,b∈R,若a->0,则下列不等式中正确的是( )
A. b-a>0 B. a3+b3<0 C. a2-b2<0 D. a+b>0
方
法
总结
核心素养 之 逻辑推理 + 数据分析
问
题
解
答
(1)选D 注意到≥-b
(2)选D 因为-c>-d >0,所以>>0, 所以 a()>b()>0
在不等式推导过程中,常用到的两个结论:
1) ≥±x 2) a>b>0时,>>0
(2)若a>b>0,c
3.已知12
法
总结
核心素养 之 逻辑推理 + 数据分析
问
题
解
答
因为15
两个正数的倒数具有反序性.
知识篇
素养篇
思维篇
2.1.2 不等式的性质
1.设a>0, 不等式-c < ax+b < c的解集是{x|-2
数学思想 之 转化与化归
问
题
解
答
方法总结
由-c < ax+b < c得-b-c c-b
又因为a>0, 所以
由已知,有, =1
解得:=,= , 所以a:b:c=2 : 1: 3
解不等式过程中的每一步化归,都用到不等式的性质;运用不等式的性质时,要检查性质的前提条件.
数学思想 之 转化与化归
问
题
解
答
2.已知a,b,c∈R,a+b+c=0, abc<0,求证:>0.
证明:由a+b+c=0,abc<0知 a,b,c中两正一负;
不妨设a>0,b>0, c<0 ; 则
===
因为 -c=a+b>0 ,所以 c2=(a+b)2>ab
所以 -c2+ab<0, 又abc<0 , 所以
方法
对于轮换式,可以作出具体的假设,以利于进一步推导.
3.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且
三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分
别为x,y,z,且x
A.ax+by+cz B.az+by+cx C.ay+bz+cx D.ay+bx+cz
数学思想 之 极端思想
问
题
解
答
选B
根据极端思想,用粉刷费用最低的涂料粉刷面积最大的房间,且用粉刷费用最高的涂料粉刷面积最小的房间,这样所需总费用最低,最低总费用为(az+by+cx)元.
可以用作差比较法加以验证.
注意:根据正数同向可乘性能得到的是最高的总费用;另一种极端情况就能得到最低的总费用.
方法总结
4.已知-2
问
题
解
答
设m=a+b, n=a-b, 则-2
又a+5b=3m-2n,所以-14
方法总结
5.若-10
问
题
解
答
1)当a≥0时,+b=a+b;
由0≤a<8, 0
由0<-a<10, -10
1.目标式带有绝对值的,要分类讨论;
2 .两个变量取值有关联时,要注意其对目标式的影响.
方法总结
课堂小结
一、本节课学习的新知识
不等式的性质
不等式性质的应用
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学运算
三、本节课训练的数学思想方法
转化与化归
课堂小结
分类讨论
极端思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
