2.5 角平分线的性质 教学课件(共29张PPT)青岛版八年级数学上册
文档属性
| 名称 | 2.5 角平分线的性质 教学课件(共29张PPT)青岛版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
课程名称:角平分线的性质
学科:数学
年级:八年级
上/下册:上册
版本:青岛版
主讲教师:
工作单位:
2.5角平分线的性质
青岛版数学八年级上册
情境导入
如图,在两条铁路之间有两个村庄A,B,现欲建一个中转站C,使得C到两条铁路的距离相等,且C到A,B两个村庄的距离也相等,试确定中转站C的位置.
学习目标
1.通过折纸活动,探索角的轴对称性质;
2.通过折一折,猜一猜,证一证的活动,探索角平分线的性质定理和判定定理,并加以证明,会进行简单的应用和综合运用;
3.通过分析角平分仪的原理,探究用尺规作角的平分线的方法,能从实际问题中建立数学模型,解决实际问题.
知识回顾
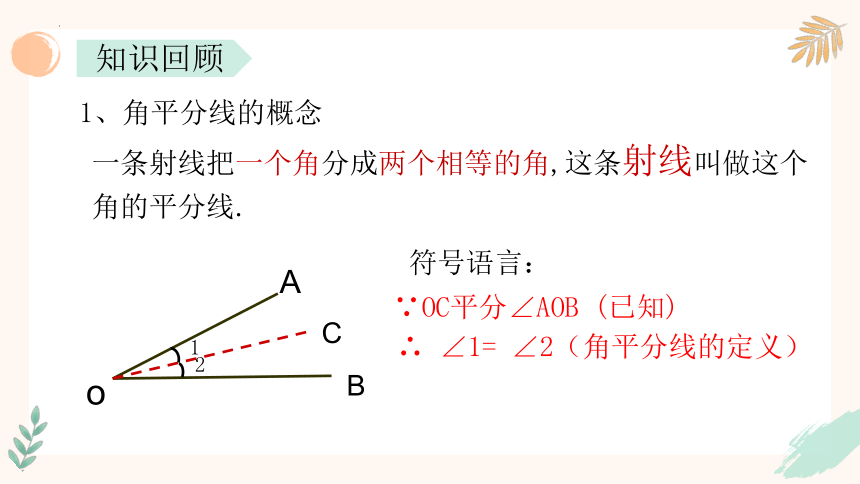
1、角平分线的概念
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
o
B
C
A
1
2
符号语言:
∴ ∠1= ∠2(角平分线的定义)
∵OC平分∠AOB (已知)
知识回顾
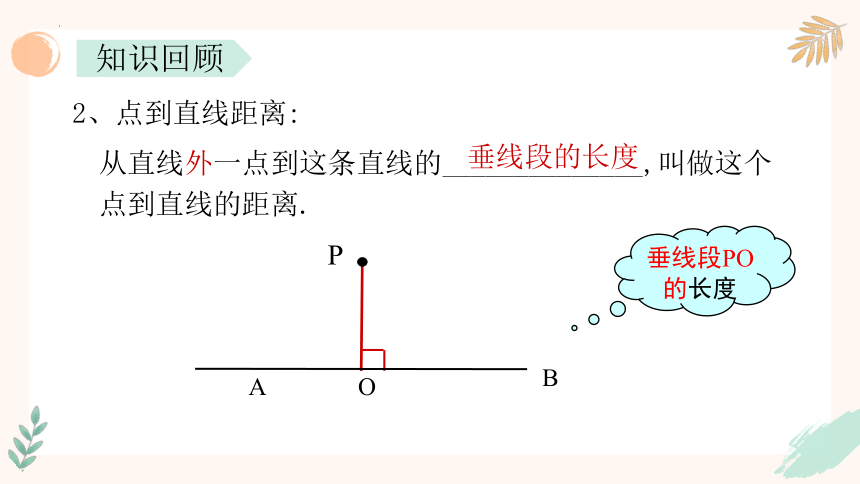
2、点到直线距离:
从直线外一点到这条直线的______________,叫做这个点到直线的距离.
垂线段PO的长度
O
P
A
B
垂线段的长度
新知探究
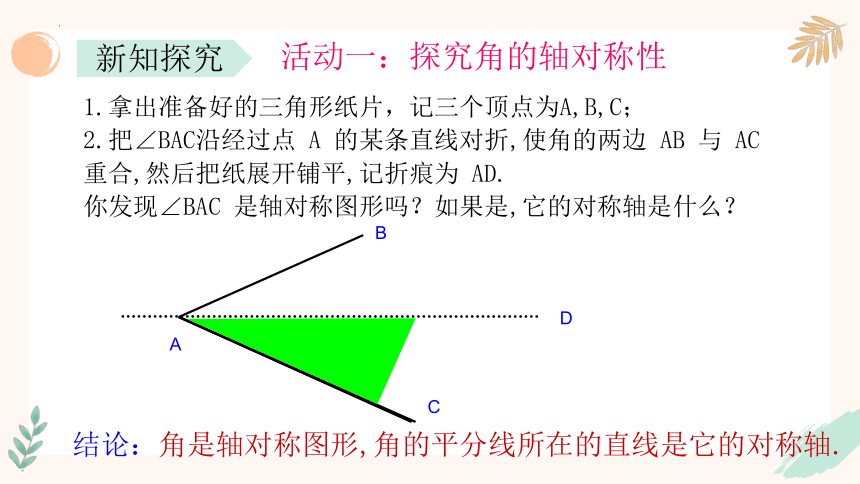
活动一:探究角的轴对称性
1.拿出准备好的三角形纸片,记三个顶点为A,B,C;
2.把∠BAC沿经过点 A 的某条直线对折,使角的两边 AB 与 AC 重合,然后把纸展开铺平,记折痕为 AD.
你发现∠BAC 是轴对称图形吗?如果是,它的对称轴是什么?
C
B
A
D
结论:角是轴对称图形,角的平分线所在的直线是它的对称轴.
D
新知探究
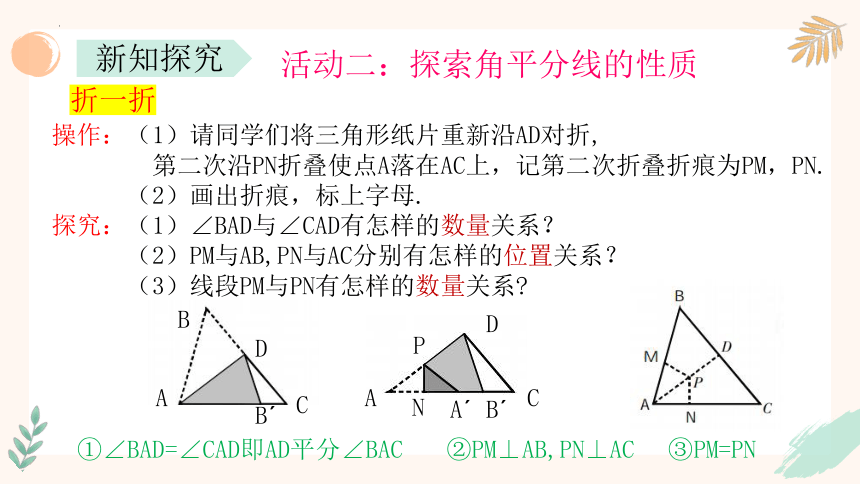
活动二:探索角平分线的性质
操作:(1)请同学们将三角形纸片重新沿AD对折,
第二次沿PN折叠使点A落在AC上,记第二次折叠折痕为PM,PN.
(2)画出折痕,标上字母.
探究:(1)∠BAD与∠CAD有怎样的数量关系?
(2)PM与AB,PN与AC分别有怎样的位置关系?
(3)线段PM与PN有怎样的数量关系
折一折
①∠BAD=∠CAD即AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
A
B
C
D
B
A
C
D
P
A
N
B
①AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
新知探究
猜一猜
角平分线有什么性质呢?请从以下三个关系中任选两个作为条件,一个作为结论,看看你能写出哪些组合,并加以证明.
组合方式:
①②推③
①③推②
②③推①
活动二:探索角平分线的性质
C
B
M
A
P
N
D
1
2
新知探究
证一证
已知:AD是∠BAC的角平分线,点P是AD上任意一点,PM⊥AB,PN⊥AC.
求证:PM=PN
C
B
M
A
P
N
D
1
2
∵AD平分∠BAC
∴ ∠1=∠2
∵PM⊥AB , PN⊥AC
∴ ∠ AMP=∠ANP=90
在△AMP与△ANP中
∵ ∠1= ∠2
∠ AMP=∠ANP
AP=AP
∴ △AMP ≌ △ANP(AAS)
∴PM=PN
证明:
结论:角平分线上的点,到这个角的两边的距离相等.
①AD平分∠BAC
②PM⊥AB,PN⊥AC
③PM=PN
请同学们试着用文字语言描述上述结论?
活动二:探索角平分线的性质
新知探究
C
B
M
A
P
N
D
角平分线的性质:
角平分线上的点,到这个角的两边的距离相等.
∵AD平分∠BAC,P在AD上
PM⊥AB ,PN⊥AC
∴PM=PN
②角平分线的性质为证明线段相等提供了新思路.
符号语言:
①一平分,两垂直得一相等.
注意:
判断正误,并说明理由:
(1)如图,P是∠AOB的平分线OC上的一点,D、E分别在OA、OB上,
则PD=PE. ( )
(2)如图,P在射线OC上,PD⊥OA,PE⊥OB,则PD=PE.( )
(3)如图,在∠AOB的平分线OC上任取一点P,若P到OA
的距离为3cm,则P到OB的距离边为3cm. ( )
(1题)
(2题)
(3题)
×
√
×
新知巩固
第1题图
第2题图
第3题图
缺少“垂直距离”这一条件
缺少“角平分线”这一条件
用一用
①AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
新知探究
猜一猜
角平分线有什么性质呢?请从以下三个关系中任选两个作为条件,一个作为结论,看看你能写出哪些组合,并加以证明.
组合方式:
①②推③
①③推②
②③推①
活动三:探索角平分线的判定
C
B
M
A
P
N
D
1
2
角的内部到角的两边距离相等的点在角的平分线上.
新知探究
结论:
已知:点P在∠BAC内部,且PM⊥AB,PN⊥AC,PM=PN.
求证:点P在∠BAC的平分线上.
C
B
M
A
P
N
D
1
2
证明: ∵PM⊥AB PN⊥AC
∴ ∠ AMP=∠ANP=90
在Rt△AMP与Rt△ANP中
PM=PN
AP=AP
∴ Rt△AMP ≌ Rt△ANP(HL)
∴ ∠1= ∠2
∴AD平分∠BAC 即点P在∠BAC的平分线上.
证一证
①AD平分∠BAC
②PM⊥AB,PN⊥AC
③PM=PN
请同学们试着用文字语言描述上述结论?
活动三:探索角平分线的判定
角的内部到角的两边距离相等的点在角的平分线上.
新知探究
C
B
M
A
P
N
D
角平分线的判定:
∵PM⊥AB ,PN⊥AC
PM=PN
∴AD平分∠BAC
②角平分线的判定为证明角相等提供了新的依据.
符号语言:
①一相等,两垂直得一平分.
注意:
①AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
新知探究
猜一猜
角平分线有什么性质呢?请从以下三个关系中任选两个作为条件,一个作为结论,看看你能写出哪些组合,并加以证明.
组合方式:
①②推③
①③推②
②③推①
C
B
M
A
P
N
D
1
2
新知探究
小组合作交流:
能由已知条件证明PM⊥AB,PN⊥AC吗?说明理由.
C
B
M
A
P
N
D
1
2
证一证
①AD平分∠BAC
②PM⊥AB,PN⊥AC
③PM=PN
M
N
∠1=∠2
PM=PN
AP=AP
边边角推不出全等!
图形 名称 图形语言 文字语言 符号语言 关键词
角平分线 性质定理
判定定理
P
C
∵OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
∴PD=PE
角的平分线上的点到角的两边的距离相等.
一平分,
两垂直,
得一相等.
P
C
∴OP平分∠AOB
∵PD=PE
PD⊥OA于D
PE⊥OB于E
角的内部到角的两边距离相等的点在角的平分线上.
一相等,
两垂直,
得一平分.
归纳小结
(1题)
(2题)
(3题)
新知应用
1. 如图,△ABC的角平分线BM,CN相交于点P
求证:点P到三角形三边AB,BC,AC的距离相等.
证明:分别过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F
∵BM平分∠ABC,PD⊥AB,PE⊥BC
∴PD=PE
∵CN平分∠ACB,PE⊥BC,PF⊥AC
∴PE=PF
∴PD=PE=PF
即点P到三边的距离相等.
∟
∟
∟
D
E
F
总结:遇到角平分线常作的辅助线
——过角平分线上一点向这个角的两边作垂线.
2. 如图,P 是∠AOB 内部的一点,PE⊥OA,PF⊥OB,垂足分别为点 E,F,且PE = PF . Q是 OP 上的任意一点, QM⊥OA, QN⊥OB,垂足分别为点 M 和 N . QM与QN 相等吗?为什么?
新知应用
证明:
∵ PE⊥OA, PF⊥OB, PE=PF
∴ OP为∠AOB的平分线
∵ QM⊥OA,QN⊥OB
∴ QM=QN
相等
(角平分线的判定)
(角平分线的性质)
新知探究
活动四:探索用尺规作角的平分线
如图,是一个角平分仪,其中OA=OB,AC=BC.将点O放在角的顶点,OA和OB沿着角的两边放下,过O,C两点作射线OC,OC就是角平分线,你能说明它的道理吗
O
B
C
A
其依据是SSS,两全等三角形的
对应角相等.
【思考】如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗?
A
B
O
请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.
提示
(1)已知什么?求作什么?
(2)仪器的顶点与角的顶点重合,且仪器的两边OA,OB相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,AC=BC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
新知探究
活动四:探索用尺规作角的平分线
O
B
C
A
A
B
M
N
C
已知: ∠AOB.
求作:∠AOB的平分线.
仔细观察步骤
作角平分线是最基本的尺规作图,大家一定要掌握噢!
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN 的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
半径为什么要大于 MN?
新知探究
活动四:探索用尺规作角的平分线
O
如图,在两条铁路之间有两个村庄A,B,现欲建一个中转站C,使得C到两条铁路的距离相等,且C到A,B两个村庄的距离也相等,试确定点C的位置.
问题解决
C
课堂小结
角的平分线的性质
会用尺规作图法作出一个已知角的平分线
性质
作图
角平分线上的点到角的两边的距离相等
利用角的平分线的性质解决实际问题
判定
角的内部到角的两边距离相等的点在角的平分线上
角是轴对称图形,对称轴是角平分线所在的直线
应用
达标检测
1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF=______ 度,BE= .
60
B F
E
B
D
F
A
C
G
2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
SSS
ASA
AAS
角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
达标检测
达标检测
4.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
证明:
再见!
课程名称:角平分线的性质
学科:数学
年级:八年级
上/下册:上册
版本:青岛版
主讲教师:
工作单位:
2.5角平分线的性质
青岛版数学八年级上册
情境导入
如图,在两条铁路之间有两个村庄A,B,现欲建一个中转站C,使得C到两条铁路的距离相等,且C到A,B两个村庄的距离也相等,试确定中转站C的位置.
学习目标
1.通过折纸活动,探索角的轴对称性质;
2.通过折一折,猜一猜,证一证的活动,探索角平分线的性质定理和判定定理,并加以证明,会进行简单的应用和综合运用;
3.通过分析角平分仪的原理,探究用尺规作角的平分线的方法,能从实际问题中建立数学模型,解决实际问题.
知识回顾
1、角平分线的概念
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
o
B
C
A
1
2
符号语言:
∴ ∠1= ∠2(角平分线的定义)
∵OC平分∠AOB (已知)
知识回顾
2、点到直线距离:
从直线外一点到这条直线的______________,叫做这个点到直线的距离.
垂线段PO的长度
O
P
A
B
垂线段的长度
新知探究
活动一:探究角的轴对称性
1.拿出准备好的三角形纸片,记三个顶点为A,B,C;
2.把∠BAC沿经过点 A 的某条直线对折,使角的两边 AB 与 AC 重合,然后把纸展开铺平,记折痕为 AD.
你发现∠BAC 是轴对称图形吗?如果是,它的对称轴是什么?
C
B
A
D
结论:角是轴对称图形,角的平分线所在的直线是它的对称轴.
D
新知探究
活动二:探索角平分线的性质
操作:(1)请同学们将三角形纸片重新沿AD对折,
第二次沿PN折叠使点A落在AC上,记第二次折叠折痕为PM,PN.
(2)画出折痕,标上字母.
探究:(1)∠BAD与∠CAD有怎样的数量关系?
(2)PM与AB,PN与AC分别有怎样的位置关系?
(3)线段PM与PN有怎样的数量关系
折一折
①∠BAD=∠CAD即AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
A
B
C
D
B
A
C
D
P
A
N
B
①AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
新知探究
猜一猜
角平分线有什么性质呢?请从以下三个关系中任选两个作为条件,一个作为结论,看看你能写出哪些组合,并加以证明.
组合方式:
①②推③
①③推②
②③推①
活动二:探索角平分线的性质
C
B
M
A
P
N
D
1
2
新知探究
证一证
已知:AD是∠BAC的角平分线,点P是AD上任意一点,PM⊥AB,PN⊥AC.
求证:PM=PN
C
B
M
A
P
N
D
1
2
∵AD平分∠BAC
∴ ∠1=∠2
∵PM⊥AB , PN⊥AC
∴ ∠ AMP=∠ANP=90
在△AMP与△ANP中
∵ ∠1= ∠2
∠ AMP=∠ANP
AP=AP
∴ △AMP ≌ △ANP(AAS)
∴PM=PN
证明:
结论:角平分线上的点,到这个角的两边的距离相等.
①AD平分∠BAC
②PM⊥AB,PN⊥AC
③PM=PN
请同学们试着用文字语言描述上述结论?
活动二:探索角平分线的性质
新知探究
C
B
M
A
P
N
D
角平分线的性质:
角平分线上的点,到这个角的两边的距离相等.
∵AD平分∠BAC,P在AD上
PM⊥AB ,PN⊥AC
∴PM=PN
②角平分线的性质为证明线段相等提供了新思路.
符号语言:
①一平分,两垂直得一相等.
注意:
判断正误,并说明理由:
(1)如图,P是∠AOB的平分线OC上的一点,D、E分别在OA、OB上,
则PD=PE. ( )
(2)如图,P在射线OC上,PD⊥OA,PE⊥OB,则PD=PE.( )
(3)如图,在∠AOB的平分线OC上任取一点P,若P到OA
的距离为3cm,则P到OB的距离边为3cm. ( )
(1题)
(2题)
(3题)
×
√
×
新知巩固
第1题图
第2题图
第3题图
缺少“垂直距离”这一条件
缺少“角平分线”这一条件
用一用
①AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
新知探究
猜一猜
角平分线有什么性质呢?请从以下三个关系中任选两个作为条件,一个作为结论,看看你能写出哪些组合,并加以证明.
组合方式:
①②推③
①③推②
②③推①
活动三:探索角平分线的判定
C
B
M
A
P
N
D
1
2
角的内部到角的两边距离相等的点在角的平分线上.
新知探究
结论:
已知:点P在∠BAC内部,且PM⊥AB,PN⊥AC,PM=PN.
求证:点P在∠BAC的平分线上.
C
B
M
A
P
N
D
1
2
证明: ∵PM⊥AB PN⊥AC
∴ ∠ AMP=∠ANP=90
在Rt△AMP与Rt△ANP中
PM=PN
AP=AP
∴ Rt△AMP ≌ Rt△ANP(HL)
∴ ∠1= ∠2
∴AD平分∠BAC 即点P在∠BAC的平分线上.
证一证
①AD平分∠BAC
②PM⊥AB,PN⊥AC
③PM=PN
请同学们试着用文字语言描述上述结论?
活动三:探索角平分线的判定
角的内部到角的两边距离相等的点在角的平分线上.
新知探究
C
B
M
A
P
N
D
角平分线的判定:
∵PM⊥AB ,PN⊥AC
PM=PN
∴AD平分∠BAC
②角平分线的判定为证明角相等提供了新的依据.
符号语言:
①一相等,两垂直得一平分.
注意:
①AD平分∠BAC
③PM=PN
②PM⊥AB,PN⊥AC
新知探究
猜一猜
角平分线有什么性质呢?请从以下三个关系中任选两个作为条件,一个作为结论,看看你能写出哪些组合,并加以证明.
组合方式:
①②推③
①③推②
②③推①
C
B
M
A
P
N
D
1
2
新知探究
小组合作交流:
能由已知条件证明PM⊥AB,PN⊥AC吗?说明理由.
C
B
M
A
P
N
D
1
2
证一证
①AD平分∠BAC
②PM⊥AB,PN⊥AC
③PM=PN
M
N
∠1=∠2
PM=PN
AP=AP
边边角推不出全等!
图形 名称 图形语言 文字语言 符号语言 关键词
角平分线 性质定理
判定定理
P
C
∵OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
∴PD=PE
角的平分线上的点到角的两边的距离相等.
一平分,
两垂直,
得一相等.
P
C
∴OP平分∠AOB
∵PD=PE
PD⊥OA于D
PE⊥OB于E
角的内部到角的两边距离相等的点在角的平分线上.
一相等,
两垂直,
得一平分.
归纳小结
(1题)
(2题)
(3题)
新知应用
1. 如图,△ABC的角平分线BM,CN相交于点P
求证:点P到三角形三边AB,BC,AC的距离相等.
证明:分别过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F
∵BM平分∠ABC,PD⊥AB,PE⊥BC
∴PD=PE
∵CN平分∠ACB,PE⊥BC,PF⊥AC
∴PE=PF
∴PD=PE=PF
即点P到三边的距离相等.
∟
∟
∟
D
E
F
总结:遇到角平分线常作的辅助线
——过角平分线上一点向这个角的两边作垂线.
2. 如图,P 是∠AOB 内部的一点,PE⊥OA,PF⊥OB,垂足分别为点 E,F,且PE = PF . Q是 OP 上的任意一点, QM⊥OA, QN⊥OB,垂足分别为点 M 和 N . QM与QN 相等吗?为什么?
新知应用
证明:
∵ PE⊥OA, PF⊥OB, PE=PF
∴ OP为∠AOB的平分线
∵ QM⊥OA,QN⊥OB
∴ QM=QN
相等
(角平分线的判定)
(角平分线的性质)
新知探究
活动四:探索用尺规作角的平分线
如图,是一个角平分仪,其中OA=OB,AC=BC.将点O放在角的顶点,OA和OB沿着角的两边放下,过O,C两点作射线OC,OC就是角平分线,你能说明它的道理吗
O
B
C
A
其依据是SSS,两全等三角形的
对应角相等.
【思考】如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗?
A
B
O
请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.
提示
(1)已知什么?求作什么?
(2)仪器的顶点与角的顶点重合,且仪器的两边OA,OB相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,AC=BC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
新知探究
活动四:探索用尺规作角的平分线
O
B
C
A
A
B
M
N
C
已知: ∠AOB.
求作:∠AOB的平分线.
仔细观察步骤
作角平分线是最基本的尺规作图,大家一定要掌握噢!
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN 的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
半径为什么要大于 MN?
新知探究
活动四:探索用尺规作角的平分线
O
如图,在两条铁路之间有两个村庄A,B,现欲建一个中转站C,使得C到两条铁路的距离相等,且C到A,B两个村庄的距离也相等,试确定点C的位置.
问题解决
C
课堂小结
角的平分线的性质
会用尺规作图法作出一个已知角的平分线
性质
作图
角平分线上的点到角的两边的距离相等
利用角的平分线的性质解决实际问题
判定
角的内部到角的两边距离相等的点在角的平分线上
角是轴对称图形,对称轴是角平分线所在的直线
应用
达标检测
1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF=______ 度,BE= .
60
B F
E
B
D
F
A
C
G
2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
SSS
ASA
AAS
角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
达标检测
达标检测
4.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
证明:
再见!
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
