精编人教版第二章整式的加减重难点题型汇总第二部分(含解析)
文档属性
| 名称 | 精编人教版第二章整式的加减重难点题型汇总第二部分(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 00:00:00 | ||
图片预览




文档简介
精编人教版第二章整式的加减重难点题型汇总及答案解析
第二部分(第一章共二个部分)
小专题6 整式的加减(二)不含某些项问题讨论
小专题7 整式的加减(三)绝对值的化简
小专题8 整式的加减(四)整式加减的实际应用
小专题9 整式的加减(五)整式加减的综合应用
第二章整式的加减
小专题6 整式的加减(二)不含某些项问题讨论
[方法技巧]不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
[例1]已知关于x和y的代数式mx4+4nxy3+3x4-xy3+2x-xy+1不含四次项,求m2-4n的值.
[例2]若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x所取的值无关,
求代数式2a3-2b2-(4a3-2b2)的值.
[方法小结]
1.对于给出的多项式,能合并的先要合并;
2.不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
1.若关于x,y的多项式mx3+3nxy2+2x3-xy2+y不含三次项,求2m+3n的值.
2.已知A=2x2+4xy-2x-3,B=-x2+xy+2,且3A+6B的值与x无关,你能求出字母 y 的值吗?
3.若代数式(2x2+ax-y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,那么请你求出3(a2-ab-b2)-(4a2+ab+b2)的值.
小专题7 整式的加减(三)绝对值的化简
[方法技巧]零点讨论法化简绝对值.
[例1]有理数a,b在数轴上的对应点位置如图所示:
试化简|a|-2|a+b-1||b-a-1|.
[例2]当x在什么范围时,|x-3|+|3-5x|+6x为定值?并写出这个定值.
[方法小结]
1.化简绝对值,就是根据绝对值的代数意义,一个正数的绝对值等于它本身,一个负数的绝对值等于它的相反数,零的绝对值是零:
2.通常用零点讨论法化简含多个绝对值的式子.
1.|x+1|+|x-2|的最小值为_______,此时x的取值是____________;
2.已知如图,数轴上有A,B,C三点分别对应有理数a,b,c,若|a|>|b|>|c|,试化简:3|b-c|-2|a+2b|+|b+c|.
小专题8 整式的加减(四)整式加减的实际应用
[方法技巧]挖掘隐含线段的关系,表达周长与面积.
[例]如图所示,用三种正方形六个和一个缺角的长方形AFHGKE拼成长方形ABCD,其中GH=a,GK=2,设BF=x.
(1)DM=_______;(用含x和a的代数式表示)
(2)求长方形ABCD的周长.(用含x和a的代数式表示)
[方法小结]
1.挖掘线段间的隐含关系,准确表示线段间的关系;
2.注意组合图形的周长和面积表达式.
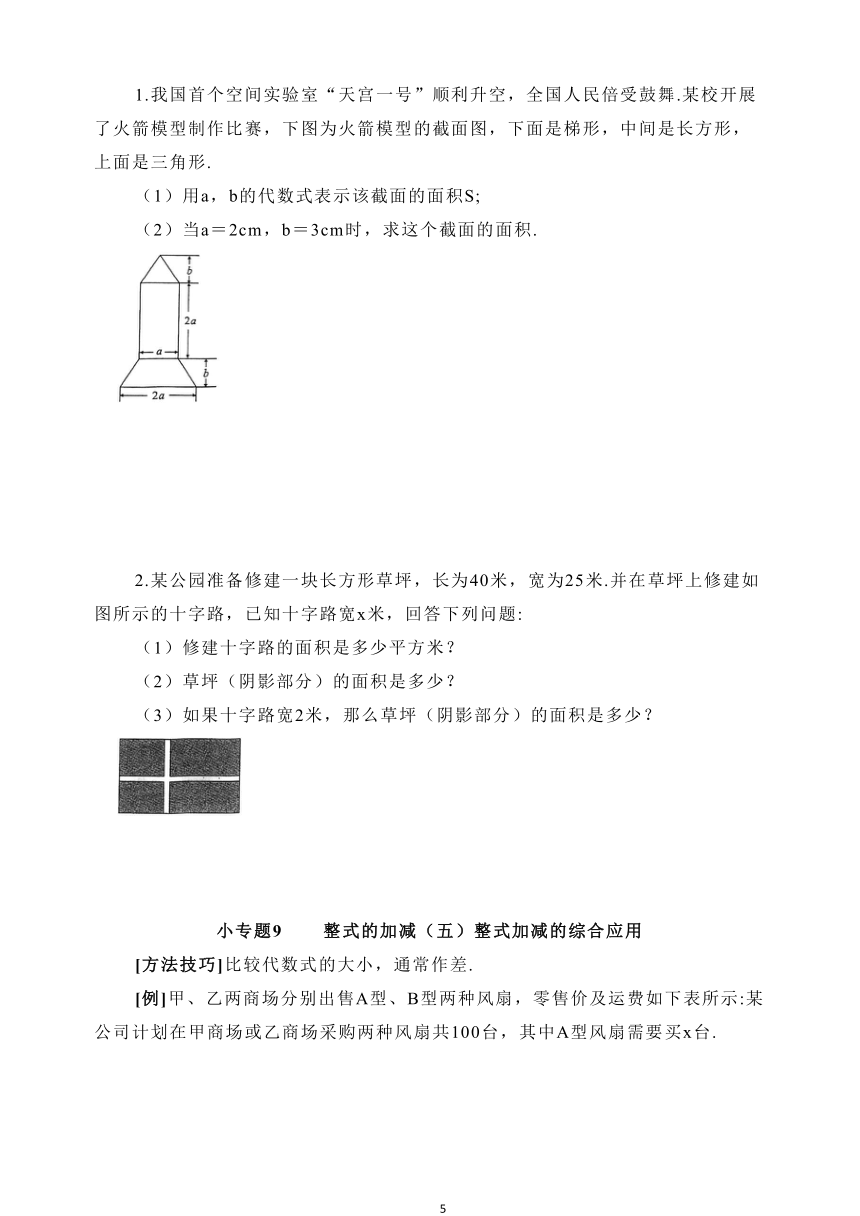
1.我国首个空间实验室“天宫一号”顺利升空,全国人民倍受鼓舞.某校开展了火箭模型制作比赛,下图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
(1)用a,b的代数式表示该截面的面积S;
(2)当a=2cm,b=3cm时,求这个截面的面积.
2.某公园准备修建一块长方形草坪,长为40米,宽为25米.并在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题:
(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?
小专题9 整式的加减(五)整式加减的综合应用
[方法技巧]比较代数式的大小,通常作差.
[例]甲、乙两商场分别出售A型、B型两种风扇,零售价及运费如下表所示:某公司计划在甲商场或乙商场采购两种风扇共100台,其中A型风扇需要买x台.
(1)请用含x的代数式分别表示在两家商场购买风扇所需要的总费用(总费用=购买价+运费);
(2)通过计算发现,在甲商场购买风扇的总费用比在乙商场购买风扇的总费用要低,且低的费用与购买A型风扇的数量无关,请求出a的值及总费用低多少?
[方法小结]
1.比较代数式的大小,通常作差;
2.在销售问题中,注意费用的组成部分,灵活表达式子.
1.为了丰富工会活动,某客户将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付费.
某客户要到该商场购买乒乓球拍20副,乒乓球x盒(x>20且为整数)
(1)若该客户按方案一购买,需付款__________元(用含x的代数式表示);
若该客户按方案二购买,需付款__________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
参考答案及解析:
小专题6 整式的加减(二)不含某些项问题讨论
[方法技巧]不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
[例1]已知关于x和y的代数式mx4+4nxy3+3x4-xy3+2x-xy+1不含四次项,求m2-4n的值.
分析:首先分清哪些是四次项,哪些是同类项,能合并的先合并;所谓不含四次项,就是四次项对应的系数为0.
解答:
解:mx4+4nxy3+3x4-xy3+2x-xy+1
=(m+3)x4+(4n-1)xy3+2x-xy+1.
因为代数式中不含四次项,所以m+3=0且4n-1=0.
解得,m=-3,.所以m2-4n=9-1=8.
[例2]若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x所取的值无关,求代数式2a3-2b2-(4a3-2b2)的值.
分析:先去括号化简,(2x2+ax-y+6)-(2bx2-3x+5y-1)=2x2+ax-y+6-2bx2+3x-5y+1=2(1-b)x2+(a+3)x-6y+7
与字母 x 的取值无关,就是含 x 项对应的系数为 0,从而得到 a, b 方程,求出 a, b 的值,最后化简求值.
解答:
解:∵(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2(1-b)x2+(a+3)x-6y+7与字母x所取的值无关,
∴1-b=0,a+3=0,∴b=1,a=-3,
∴原式=-2a3=54
[方法小结]
1.对于给出的多项式,能合并的先要合并;
2.不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
1.若关于x,y的多项式mx3+3nxy2+2x3-xy2+y不含三次项,求2m+3n的值.
解答:
解:∵mx3+3nxy2+2x3-xy2+y=(m+2)x3+(3n-1)xy2+y不含三次项,
∴m+2=0,3n-1=0,∴m=-2,3n=1,
∴2m+3n=-3.
2.已知A=2x2+4xy-2x-3,B=-x2+xy+2,且3A+6B的值与x无关,你能求出字母 y 的值吗?
解答:
解:3A+6B=6x(3y-1)+3与x无关,则3y-1=0,∴
3.若代数式(2x2+ax-y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,那么请你求出3(a2-ab-b2)-(4a2+ab+b2)的值.
解答:
解:(2x2+ax-y+b)-(2bx2-3x+5y-1)
=(2-2b)x2+(a+3)x+(-6y+b+1),其值与x的取值无关,
∴2-2b=0,a+3=0,∴a=-3,b=1,
∴原式=-a2-4ab-4b2=-1
小专题7 整式的加减(三)绝对值的化简
[方法技巧]零点讨论法化简绝对值.
[例1]有理数a,b在数轴上的对应点位置如图所示:
试化简|a|-2|a+b-1||b-a-1|.
分析:根据相反数的意义,我们可以在数轴上标出-a与-b,a<-1<-b<0<b<1<-a,从而得到 a<0, a+b-1<0, b-a-1>0,利用绝对值的意义,去掉绝对值,进而化简.
解答:
解:∵a<-1<-b<0<b<1<-a,
∴原式=-a+2(a+b-1)(b-a-1)
[例2]当x在什么范围时,|x-3|+|3-5x|+6x为定值?并写出这个定值.
分析:使绝对值为0的x值称为零点,显然零点是或3,
解答:
解:(1)当x≤时,|x-3|+|3-5x|+6x=-(x-3)+(3-5x)+6x=-x+3+3-5x+6x=6;
(2)当≤x≤3时,|x-3|+|3-5x|+6x=-(x-3)-(3-5x)+6x
=-x+3-3+5x+6x=10x;
(3)当x≥3时,|x-3|+|3-5x|+6x=(x-3)-(3-5x)+6x
=x-3-3+5x+6x=12x-6.
当x≤时,|x-3|+|3-5x|+6x为定值,定值为6.
[方法小结]
1.化简绝对值,就是根据绝对值的代数意义,一个正数的绝对值等于它本身,一个负数的绝对值等于它的相反数,零的绝对值是零:
2.通常用零点讨论法化简含多个绝对值的式子.
1.|x+1|+|x-2|的最小值为_______,此时x的取值是____________;
解答:
解:当x<-1,原式=-x-1+2-x=1-2x>3;
当-1≤x≤2时,原式=x+1+2-x=3;
当x>2时,原式=x+1+x-2=2x-1>3;
∴|x+1|+|x-2|的最小值为3,-1≤x≤2.
2.已知如图,数轴上有A,B,C三点分别对应有理数a,b,c,若|a|>|b|>|c|,试化简:3|b-c|-2|a+2b|+|b+c|.
解答:
解:由|a|>|b|>|c|可知,原点O在BC之间且靠近点C或在点C右边,
∴b-c<0,a+2b<0,b+c<0,
∴3|b-c|-2|a+2b|+|b+c|=3(c-b)+2(a+2b)-(b+c)=2a+2c.
小专题8 整式的加减(四)整式加减的实际应用
[方法技巧]挖掘隐含线段的关系,表达周长与面积.
[例]如图所示,用三种正方形六个和一个缺角的长方形AFHGKE拼成长方形ABCD,其中GH=a,GK=2,设BF=x.
(1)DM=_______;(用含x和a的代数式表示)
(2)求长方形ABCD的周长.(用含x和a的代数式表示)
解答:
解:(1)CM=GH+FB=a+x,则DM=KM=2(a+x)-2=2x+2a-2,
故答案为:2x+2a-2;
(2)CD=DM+CM=2x+2a-2+x+a=3x+3a-2, AD=AE+ED=3x+2+2x+2a-2=5x+2a,
则长方形ABCD的周长为2(AD+CD)=2(5x+2a)+2(3x+3a-2)=16x+10a-4.
[方法小结]
1.挖掘线段间的隐含关系,准确表示线段间的关系;
2.注意组合图形的周长和面积表达式.
1.我国首个空间实验室“天宫一号”顺利升空,全国人民倍受鼓舞.某校开展了火箭模型制作比赛,下图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
(1)用a,b的代数式表示该截面的面积S;
(2)当a=2cm,b=3cm时,求这个截面的面积.
答案:(1)S=2ab+2a2;(2)S=20cm2.
解答:
解(1)ab+2a2(a+2a)b=2ab+ 2a2;
(2)当a=2,b=3时,原式=2ab+2a2=2× 2×3+2×4=12+8=20(cm2).
2.某公园准备修建一块长方形草坪,长为40米,宽为25米.并在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题:
(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?
解:(1)40x+25x-x2=65x-x2.
答:修建十字路的面积是(65x-x2)平方米.
(2)草坪的面积为:40×25-(65x-x2)=1000-65x+x2;
(3)1000-65x+x2=1000-65×2+2×2=874(平方米).
答:草坪(阴影部分)的面积874平方米.
小专题9 整式的加减(五)整式加减的综合应用
[方法技巧]比较代数式的大小,通常作差.
[例]甲、乙两商场分别出售A型、B型两种风扇,零售价及运费如下表所示:某公司计划在甲商场或乙商场采购两种风扇共100台,其中A型风扇需要买x台.
(1)请用含x的代数式分别表示在两家商场购买风扇所需要的总费用(总费用=购买价+运费);
分析:设在甲、乙两商场购买风扇所需要的总费用分别为WA,WB,则
WA=210x+310(100-x)
陈=220x+(290+a)(100-x)
解答:
解:WA=210x+310(100-x)=-100x+31000,
WB=220x+(290+a)(100-x)=-(70+a)x+29000+100a;
(2)通过计算发现,在甲商场购买风扇的总费用比在乙商场购买风扇的总费用要低,且低的费用与购买A型风扇的数量无关,请求出a的值及总费用低多少?
分析:(1)WA=210x+310(100-x)=-100x+31000,
WB=220x+(290+a)(100-x)=-(70+a)x+29000+100a;
WB- WA 与购买 A 型风扇的数量无关,
与字母 x 的取值无关,就是含 x 项对应的系数为 0,
(2)WB-WA=-(70+a)x+29000+100a-(-100x+31000)
=(30-a)x+100a-2000,∵低的费用与购买A型风扇的数量无关,
∴30-a=0,∴a=30,(30-a)x+100a-2000=100×30-2000=1000.
∴当a=30时,在甲商场购买风扇的总费用比在乙商场购买风扇的总费用要低1000元.
[方法小结]
1.比较代数式的大小,通常作差;
2.在销售问题中,注意费用的组成部分,灵活表达式子.
1.为了丰富工会活动,某客户将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付费.
某客户要到该商场购买乒乓球拍20副,乒乓球x盒(x>20且为整数)
(1)若该客户按方案一购买,需付款__________元(用含x的代数式表示);
若该客户按方案二购买,需付款__________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
解:(1)方案一费用:(20x+1200)元;方案二费用:(18x+1440)元;
(2)当x=30时,方案一:20×30+1200=1800(元);
方案二:18×30+1440=1980(元);
所以,按方案一购买较合算;
(3)先按方案一购买20副乒乓球拍获赠送20盒乒乓球,再按方案二购买10盒乒乓球.
则20×80+20×10×90%=1780(元).
第二部分(第一章共二个部分)
小专题6 整式的加减(二)不含某些项问题讨论
小专题7 整式的加减(三)绝对值的化简
小专题8 整式的加减(四)整式加减的实际应用
小专题9 整式的加减(五)整式加减的综合应用
第二章整式的加减
小专题6 整式的加减(二)不含某些项问题讨论
[方法技巧]不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
[例1]已知关于x和y的代数式mx4+4nxy3+3x4-xy3+2x-xy+1不含四次项,求m2-4n的值.
[例2]若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x所取的值无关,
求代数式2a3-2b2-(4a3-2b2)的值.
[方法小结]
1.对于给出的多项式,能合并的先要合并;
2.不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
1.若关于x,y的多项式mx3+3nxy2+2x3-xy2+y不含三次项,求2m+3n的值.
2.已知A=2x2+4xy-2x-3,B=-x2+xy+2,且3A+6B的值与x无关,你能求出字母 y 的值吗?
3.若代数式(2x2+ax-y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,那么请你求出3(a2-ab-b2)-(4a2+ab+b2)的值.
小专题7 整式的加减(三)绝对值的化简
[方法技巧]零点讨论法化简绝对值.
[例1]有理数a,b在数轴上的对应点位置如图所示:
试化简|a|-2|a+b-1||b-a-1|.
[例2]当x在什么范围时,|x-3|+|3-5x|+6x为定值?并写出这个定值.
[方法小结]
1.化简绝对值,就是根据绝对值的代数意义,一个正数的绝对值等于它本身,一个负数的绝对值等于它的相反数,零的绝对值是零:
2.通常用零点讨论法化简含多个绝对值的式子.
1.|x+1|+|x-2|的最小值为_______,此时x的取值是____________;
2.已知如图,数轴上有A,B,C三点分别对应有理数a,b,c,若|a|>|b|>|c|,试化简:3|b-c|-2|a+2b|+|b+c|.
小专题8 整式的加减(四)整式加减的实际应用
[方法技巧]挖掘隐含线段的关系,表达周长与面积.
[例]如图所示,用三种正方形六个和一个缺角的长方形AFHGKE拼成长方形ABCD,其中GH=a,GK=2,设BF=x.
(1)DM=_______;(用含x和a的代数式表示)
(2)求长方形ABCD的周长.(用含x和a的代数式表示)
[方法小结]
1.挖掘线段间的隐含关系,准确表示线段间的关系;
2.注意组合图形的周长和面积表达式.
1.我国首个空间实验室“天宫一号”顺利升空,全国人民倍受鼓舞.某校开展了火箭模型制作比赛,下图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
(1)用a,b的代数式表示该截面的面积S;
(2)当a=2cm,b=3cm时,求这个截面的面积.
2.某公园准备修建一块长方形草坪,长为40米,宽为25米.并在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题:
(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?
小专题9 整式的加减(五)整式加减的综合应用
[方法技巧]比较代数式的大小,通常作差.
[例]甲、乙两商场分别出售A型、B型两种风扇,零售价及运费如下表所示:某公司计划在甲商场或乙商场采购两种风扇共100台,其中A型风扇需要买x台.
(1)请用含x的代数式分别表示在两家商场购买风扇所需要的总费用(总费用=购买价+运费);
(2)通过计算发现,在甲商场购买风扇的总费用比在乙商场购买风扇的总费用要低,且低的费用与购买A型风扇的数量无关,请求出a的值及总费用低多少?
[方法小结]
1.比较代数式的大小,通常作差;
2.在销售问题中,注意费用的组成部分,灵活表达式子.
1.为了丰富工会活动,某客户将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付费.
某客户要到该商场购买乒乓球拍20副,乒乓球x盒(x>20且为整数)
(1)若该客户按方案一购买,需付款__________元(用含x的代数式表示);
若该客户按方案二购买,需付款__________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
参考答案及解析:
小专题6 整式的加减(二)不含某些项问题讨论
[方法技巧]不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
[例1]已知关于x和y的代数式mx4+4nxy3+3x4-xy3+2x-xy+1不含四次项,求m2-4n的值.
分析:首先分清哪些是四次项,哪些是同类项,能合并的先合并;所谓不含四次项,就是四次项对应的系数为0.
解答:
解:mx4+4nxy3+3x4-xy3+2x-xy+1
=(m+3)x4+(4n-1)xy3+2x-xy+1.
因为代数式中不含四次项,所以m+3=0且4n-1=0.
解得,m=-3,.所以m2-4n=9-1=8.
[例2]若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x所取的值无关,求代数式2a3-2b2-(4a3-2b2)的值.
分析:先去括号化简,(2x2+ax-y+6)-(2bx2-3x+5y-1)=2x2+ax-y+6-2bx2+3x-5y+1=2(1-b)x2+(a+3)x-6y+7
与字母 x 的取值无关,就是含 x 项对应的系数为 0,从而得到 a, b 方程,求出 a, b 的值,最后化简求值.
解答:
解:∵(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2(1-b)x2+(a+3)x-6y+7与字母x所取的值无关,
∴1-b=0,a+3=0,∴b=1,a=-3,
∴原式=-2a3=54
[方法小结]
1.对于给出的多项式,能合并的先要合并;
2.不含某项或与字母取值无关,就是这项或含该字母的项的系数为零.
1.若关于x,y的多项式mx3+3nxy2+2x3-xy2+y不含三次项,求2m+3n的值.
解答:
解:∵mx3+3nxy2+2x3-xy2+y=(m+2)x3+(3n-1)xy2+y不含三次项,
∴m+2=0,3n-1=0,∴m=-2,3n=1,
∴2m+3n=-3.
2.已知A=2x2+4xy-2x-3,B=-x2+xy+2,且3A+6B的值与x无关,你能求出字母 y 的值吗?
解答:
解:3A+6B=6x(3y-1)+3与x无关,则3y-1=0,∴
3.若代数式(2x2+ax-y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,那么请你求出3(a2-ab-b2)-(4a2+ab+b2)的值.
解答:
解:(2x2+ax-y+b)-(2bx2-3x+5y-1)
=(2-2b)x2+(a+3)x+(-6y+b+1),其值与x的取值无关,
∴2-2b=0,a+3=0,∴a=-3,b=1,
∴原式=-a2-4ab-4b2=-1
小专题7 整式的加减(三)绝对值的化简
[方法技巧]零点讨论法化简绝对值.
[例1]有理数a,b在数轴上的对应点位置如图所示:
试化简|a|-2|a+b-1||b-a-1|.
分析:根据相反数的意义,我们可以在数轴上标出-a与-b,a<-1<-b<0<b<1<-a,从而得到 a<0, a+b-1<0, b-a-1>0,利用绝对值的意义,去掉绝对值,进而化简.
解答:
解:∵a<-1<-b<0<b<1<-a,
∴原式=-a+2(a+b-1)(b-a-1)
[例2]当x在什么范围时,|x-3|+|3-5x|+6x为定值?并写出这个定值.
分析:使绝对值为0的x值称为零点,显然零点是或3,
解答:
解:(1)当x≤时,|x-3|+|3-5x|+6x=-(x-3)+(3-5x)+6x=-x+3+3-5x+6x=6;
(2)当≤x≤3时,|x-3|+|3-5x|+6x=-(x-3)-(3-5x)+6x
=-x+3-3+5x+6x=10x;
(3)当x≥3时,|x-3|+|3-5x|+6x=(x-3)-(3-5x)+6x
=x-3-3+5x+6x=12x-6.
当x≤时,|x-3|+|3-5x|+6x为定值,定值为6.
[方法小结]
1.化简绝对值,就是根据绝对值的代数意义,一个正数的绝对值等于它本身,一个负数的绝对值等于它的相反数,零的绝对值是零:
2.通常用零点讨论法化简含多个绝对值的式子.
1.|x+1|+|x-2|的最小值为_______,此时x的取值是____________;
解答:
解:当x<-1,原式=-x-1+2-x=1-2x>3;
当-1≤x≤2时,原式=x+1+2-x=3;
当x>2时,原式=x+1+x-2=2x-1>3;
∴|x+1|+|x-2|的最小值为3,-1≤x≤2.
2.已知如图,数轴上有A,B,C三点分别对应有理数a,b,c,若|a|>|b|>|c|,试化简:3|b-c|-2|a+2b|+|b+c|.
解答:
解:由|a|>|b|>|c|可知,原点O在BC之间且靠近点C或在点C右边,
∴b-c<0,a+2b<0,b+c<0,
∴3|b-c|-2|a+2b|+|b+c|=3(c-b)+2(a+2b)-(b+c)=2a+2c.
小专题8 整式的加减(四)整式加减的实际应用
[方法技巧]挖掘隐含线段的关系,表达周长与面积.
[例]如图所示,用三种正方形六个和一个缺角的长方形AFHGKE拼成长方形ABCD,其中GH=a,GK=2,设BF=x.
(1)DM=_______;(用含x和a的代数式表示)
(2)求长方形ABCD的周长.(用含x和a的代数式表示)
解答:
解:(1)CM=GH+FB=a+x,则DM=KM=2(a+x)-2=2x+2a-2,
故答案为:2x+2a-2;
(2)CD=DM+CM=2x+2a-2+x+a=3x+3a-2, AD=AE+ED=3x+2+2x+2a-2=5x+2a,
则长方形ABCD的周长为2(AD+CD)=2(5x+2a)+2(3x+3a-2)=16x+10a-4.
[方法小结]
1.挖掘线段间的隐含关系,准确表示线段间的关系;
2.注意组合图形的周长和面积表达式.
1.我国首个空间实验室“天宫一号”顺利升空,全国人民倍受鼓舞.某校开展了火箭模型制作比赛,下图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
(1)用a,b的代数式表示该截面的面积S;
(2)当a=2cm,b=3cm时,求这个截面的面积.
答案:(1)S=2ab+2a2;(2)S=20cm2.
解答:
解(1)ab+2a2(a+2a)b=2ab+ 2a2;
(2)当a=2,b=3时,原式=2ab+2a2=2× 2×3+2×4=12+8=20(cm2).
2.某公园准备修建一块长方形草坪,长为40米,宽为25米.并在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题:
(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?
解:(1)40x+25x-x2=65x-x2.
答:修建十字路的面积是(65x-x2)平方米.
(2)草坪的面积为:40×25-(65x-x2)=1000-65x+x2;
(3)1000-65x+x2=1000-65×2+2×2=874(平方米).
答:草坪(阴影部分)的面积874平方米.
小专题9 整式的加减(五)整式加减的综合应用
[方法技巧]比较代数式的大小,通常作差.
[例]甲、乙两商场分别出售A型、B型两种风扇,零售价及运费如下表所示:某公司计划在甲商场或乙商场采购两种风扇共100台,其中A型风扇需要买x台.
(1)请用含x的代数式分别表示在两家商场购买风扇所需要的总费用(总费用=购买价+运费);
分析:设在甲、乙两商场购买风扇所需要的总费用分别为WA,WB,则
WA=210x+310(100-x)
陈=220x+(290+a)(100-x)
解答:
解:WA=210x+310(100-x)=-100x+31000,
WB=220x+(290+a)(100-x)=-(70+a)x+29000+100a;
(2)通过计算发现,在甲商场购买风扇的总费用比在乙商场购买风扇的总费用要低,且低的费用与购买A型风扇的数量无关,请求出a的值及总费用低多少?
分析:(1)WA=210x+310(100-x)=-100x+31000,
WB=220x+(290+a)(100-x)=-(70+a)x+29000+100a;
WB- WA 与购买 A 型风扇的数量无关,
与字母 x 的取值无关,就是含 x 项对应的系数为 0,
(2)WB-WA=-(70+a)x+29000+100a-(-100x+31000)
=(30-a)x+100a-2000,∵低的费用与购买A型风扇的数量无关,
∴30-a=0,∴a=30,(30-a)x+100a-2000=100×30-2000=1000.
∴当a=30时,在甲商场购买风扇的总费用比在乙商场购买风扇的总费用要低1000元.
[方法小结]
1.比较代数式的大小,通常作差;
2.在销售问题中,注意费用的组成部分,灵活表达式子.
1.为了丰富工会活动,某客户将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付费.
某客户要到该商场购买乒乓球拍20副,乒乓球x盒(x>20且为整数)
(1)若该客户按方案一购买,需付款__________元(用含x的代数式表示);
若该客户按方案二购买,需付款__________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
解:(1)方案一费用:(20x+1200)元;方案二费用:(18x+1440)元;
(2)当x=30时,方案一:20×30+1200=1800(元);
方案二:18×30+1440=1980(元);
所以,按方案一购买较合算;
(3)先按方案一购买20副乒乓球拍获赠送20盒乒乓球,再按方案二购买10盒乒乓球.
则20×80+20×10×90%=1780(元).
