全等三角形的条件复习
图片预览



文档简介
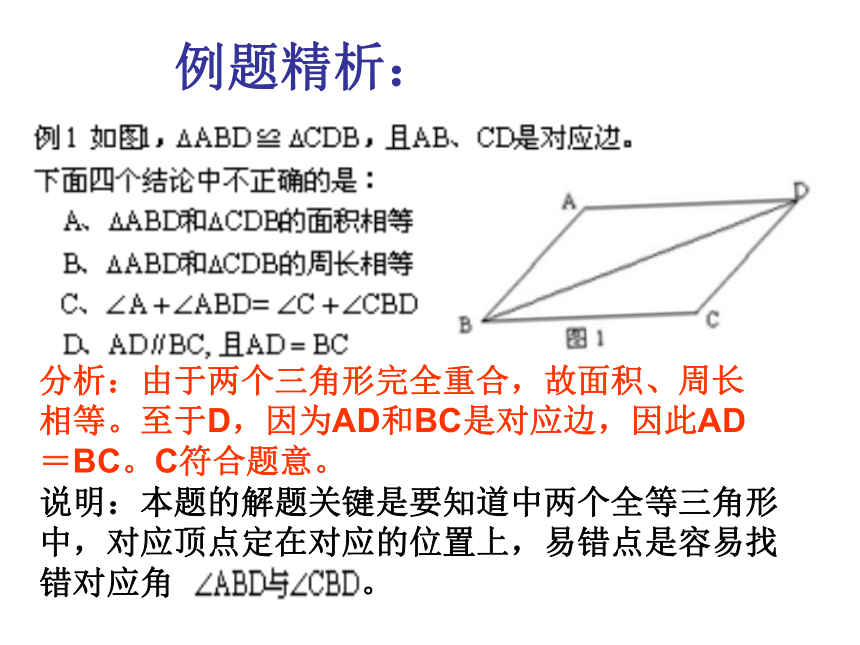
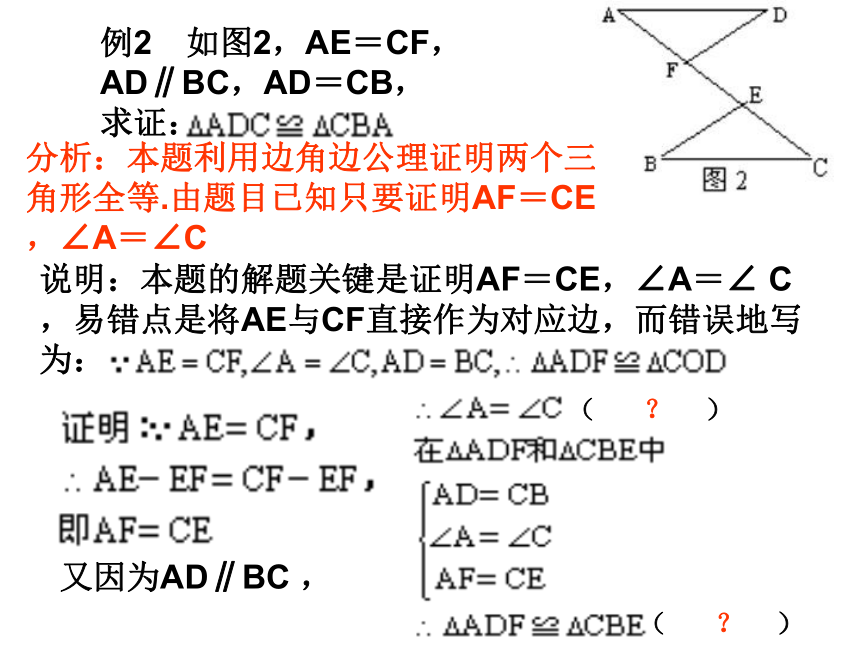
课件15张PPT。13.2三角形全等的条件复习课知识回顾:一般三角形 全等的条件:1.定义(重合)法;2.SSS;3.SAS;4.ASA;5.AAS.直角三角形 全等特有的条件:HL.包括直角三角形不包括其它形状的三角形分析:由于两个三角形完全重合,故面积、周长相等。至于D,因为AD和BC是对应边,因此AD=BC。C符合题意。说明:本题的解题关键是要知道中两个全等三角形中,对应顶点定在对应的位置上,易错点是容易找错对应角 ???????????? 。例题精析:分析:本题利用边角边公理证明两个三角形全等.由题目已知只要证明AF=CE,∠A=∠C例2 如图2,AE=CF,AD∥BC,AD=CB,
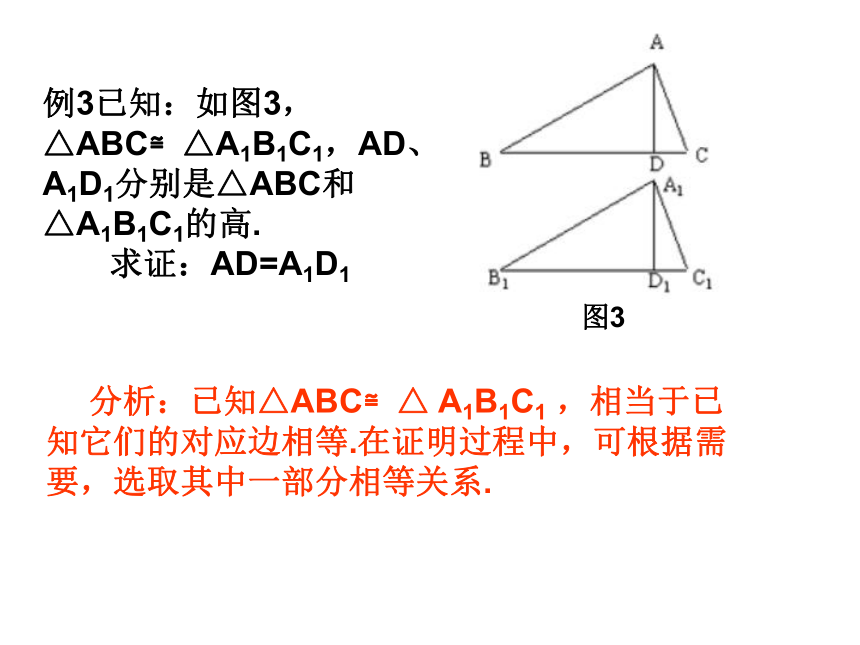
求证: ?????????????说明:本题的解题关键是证明AF=CE,∠A=∠ C,易错点是将AE与CF直接作为对应边,而错误地写为:??????????????????????????????????又因为AD∥BC ,( ? )( ? ) 分析:已知△ABC≌△ A1B1C1 ,相当于已知它们的对应边相等.在证明过程中,可根据需要,选取其中一部分相等关系.例3已知:如图3,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.
求证:AD=A1D1图3说明:本题为例2的一个延伸题目,关键是利用三角形全等的性质及判定找到相等关系.类似的题目还有角平分线相等、中线相等.
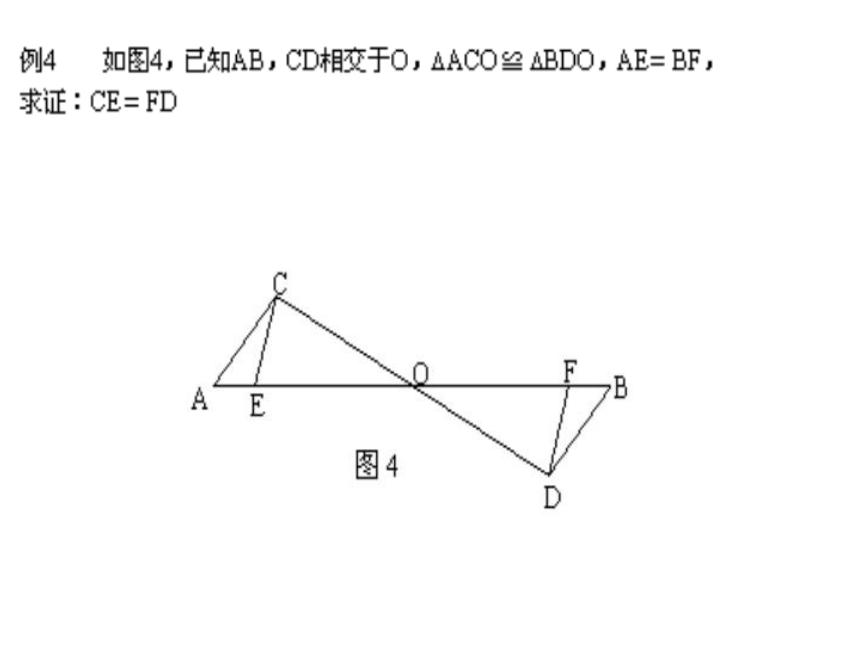
说明:本题的解题关键是证明 ???????????? ,易错点是忽视证OE=OF,而直接将证得的AO=BO作为证明 ???????????? 的条件.另外注意格式书写.分析:AB不是全等三角形的对应边,
但它通过对应边转化为AB=CD,而使AB+CD=AD-BC,可利用已知的AD与BC求得。说明:解决本题的关键是利用三角形全等的性质,得到对应边相等。例6:求证:有一条直角边和斜边上的高对应相等的两个直角三角形全等。分析:首先要分清题设和结论,然后按要求画出图形,根据题意写出、已知求证后,再写出证明过程。 已知: 如图,在Rt△ABC、Rt△ ??????? 中,∠ACB=∠ ??????? =Rt∠,BC= ?????,
CD⊥AB于D, ?????⊥ ?????于 ???,CD= ?????
求证:Rt△ABC≌Rt△
证明:在Rt△CDB和
Rt△ ????? 中
????????????????
∴Rt△CDB≌Rt△ ????????(HL)
由此得∠B=∠ ???
在△ABC与△ ???????中
?????????????????????
∴△ABC≌△ ???????(ASA)说明:文字证明题的书写格式要标准。1.如图1:△ABF≌ △CDE,∠B=30°, ∠BAE= ∠DCF=20 °.求∠EFC的度数.练习题:2 、如图2,已知:AD平分∠BAC,AB=AC,连接BD,CD,并延长相交AC、AB于F、E点.则图形中有(? )对全等三角形.
A、2 B、3 C4 D、5
C图1图23、如图3,已知:△ABC中,DF=FE,BD=CE,AF⊥BC于F,则此图中全等三角形共有(? )
A、5对 B、4对 C、3对 D2对
?????????????????????????????????????????????????????????????????????????????????????????????????????????
4、如图4,已知:在△ABC中,AD是BC边上的高,AD=BD,DE=DC,延长BE交AC于F,
求证:BF是△ABC中边上的高.
提示:关键证明△ADC≌△BFCB 5、如图5,已知:AB=CD,AD=CB,O为AC任一点,过O作直线分别交AB、CD的延长线于F、E,求证:∠E=∠F.提示:由条件易证△ABC≌△CDA 从而得知∠BAC=∠DCA ,即:AB∥CD.6、如图6,已知:∠A=90°, AB=BD,ED⊥BC于 D.
求证:AE=ED
提示:找两个全等三角形,需连结BE.图6
求证: ?????????????说明:本题的解题关键是证明AF=CE,∠A=∠ C,易错点是将AE与CF直接作为对应边,而错误地写为:??????????????????????????????????又因为AD∥BC ,( ? )( ? ) 分析:已知△ABC≌△ A1B1C1 ,相当于已知它们的对应边相等.在证明过程中,可根据需要,选取其中一部分相等关系.例3已知:如图3,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.
求证:AD=A1D1图3说明:本题为例2的一个延伸题目,关键是利用三角形全等的性质及判定找到相等关系.类似的题目还有角平分线相等、中线相等.
说明:本题的解题关键是证明 ???????????? ,易错点是忽视证OE=OF,而直接将证得的AO=BO作为证明 ???????????? 的条件.另外注意格式书写.分析:AB不是全等三角形的对应边,
但它通过对应边转化为AB=CD,而使AB+CD=AD-BC,可利用已知的AD与BC求得。说明:解决本题的关键是利用三角形全等的性质,得到对应边相等。例6:求证:有一条直角边和斜边上的高对应相等的两个直角三角形全等。分析:首先要分清题设和结论,然后按要求画出图形,根据题意写出、已知求证后,再写出证明过程。 已知: 如图,在Rt△ABC、Rt△ ??????? 中,∠ACB=∠ ??????? =Rt∠,BC= ?????,
CD⊥AB于D, ?????⊥ ?????于 ???,CD= ?????
求证:Rt△ABC≌Rt△
证明:在Rt△CDB和
Rt△ ????? 中
????????????????
∴Rt△CDB≌Rt△ ????????(HL)
由此得∠B=∠ ???
在△ABC与△ ???????中
?????????????????????
∴△ABC≌△ ???????(ASA)说明:文字证明题的书写格式要标准。1.如图1:△ABF≌ △CDE,∠B=30°, ∠BAE= ∠DCF=20 °.求∠EFC的度数.练习题:2 、如图2,已知:AD平分∠BAC,AB=AC,连接BD,CD,并延长相交AC、AB于F、E点.则图形中有(? )对全等三角形.
A、2 B、3 C4 D、5
C图1图23、如图3,已知:△ABC中,DF=FE,BD=CE,AF⊥BC于F,则此图中全等三角形共有(? )
A、5对 B、4对 C、3对 D2对
?????????????????????????????????????????????????????????????????????????????????????????????????????????
4、如图4,已知:在△ABC中,AD是BC边上的高,AD=BD,DE=DC,延长BE交AC于F,
求证:BF是△ABC中边上的高.
提示:关键证明△ADC≌△BFCB 5、如图5,已知:AB=CD,AD=CB,O为AC任一点,过O作直线分别交AB、CD的延长线于F、E,求证:∠E=∠F.提示:由条件易证△ABC≌△CDA 从而得知∠BAC=∠DCA ,即:AB∥CD.6、如图6,已知:∠A=90°, AB=BD,ED⊥BC于 D.
求证:AE=ED
提示:找两个全等三角形,需连结BE.图6
