2.3函数的应用(Ⅰ) 山东省第六届教学能手比赛课件
文档属性
| 名称 | 2.3函数的应用(Ⅰ) 山东省第六届教学能手比赛课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 82.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-12 12:50:20 | ||
图片预览



文档简介
课件9张PPT。2.3 函数的应用(Ⅰ)人教B版必修1山东师大附中
(一)确立目标,引领课堂初步掌握一次和二次函数模型的应用,会解决较简单的实际问题;
尝试运用一次和二次函数模型解决实际问题,提高数学建模的能力。
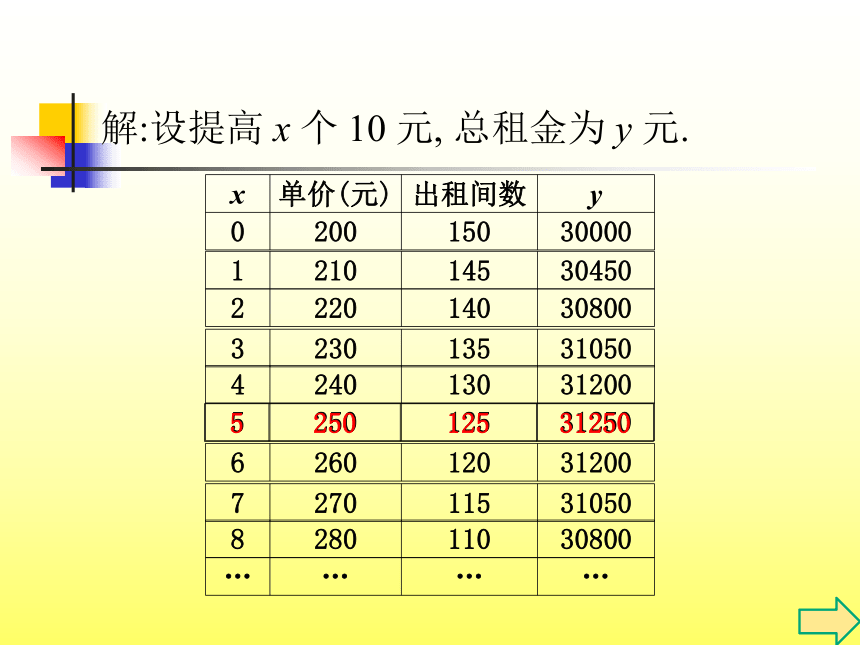
济南市某国际酒店有客房150间, 每间日房租为200元,每天都客满. 酒店欲提高档次,并提高租金, 如果每间日房租每增加10元,客房出租数就会减少5间. 若不考虑其他因素,酒店将房间租金提高到多少时,每天客房的租金总收入最高?(二)结合实例,探求新知解:设提高 x 个 10 元, 总租金为 y 元. (三)归纳整理,发展思维函数应用题的一般解题步骤(1)审题: 认真读题,正确理解题意,理顺数量 关系;
(2)建模:合理选取变量,建立实际问题中的变量 之间的函数关系,从而将实际问题转 化为函数模型问题;
(3)解模:运用有关数学知识,解决这个函数模型;
(4)还原:将所得结论转译成实际问题的解答.(四)应用新知,巩固提高巩固练习1
某单位计划用围墙围出一块矩形场地, 现有材料可筑墙的总长度为 l , 如果要使围墙围出的场地面积最大, 问矩形的长、宽各等于多少?(四)应用新知,巩固提高 巩固练习2
某列火车从北京西站开往石家庄, 全程 277 km, 火车出发 10 min 开出 13 km后, 以 120 km/h 匀速行驶. 试写出火车行驶的总路程 S 与匀速行驶的时间 t 之间的关系式, 并求火车离开北京 2 h 内行驶的路程.(五)归纳整理,布置作业小结:知识:一次、二次函数模型在实际中的应用;
步骤:审题、建模、解模、还原;
问题:审题不清,建模错误,忽略定义域和检验
思想:划归思想、函数思想.(五)归纳整理,布置作业作业:必做:教材68页 1,3,4选做:要建一个容积为8 m3,深为2 m 的长方体无盖水池, 如果池底和池壁的造价每平方米分别为 120 元和 80 元, 试求应当怎样设计, 才能使水池总造价最低?并求此最低造价.
(一)确立目标,引领课堂初步掌握一次和二次函数模型的应用,会解决较简单的实际问题;
尝试运用一次和二次函数模型解决实际问题,提高数学建模的能力。
济南市某国际酒店有客房150间, 每间日房租为200元,每天都客满. 酒店欲提高档次,并提高租金, 如果每间日房租每增加10元,客房出租数就会减少5间. 若不考虑其他因素,酒店将房间租金提高到多少时,每天客房的租金总收入最高?(二)结合实例,探求新知解:设提高 x 个 10 元, 总租金为 y 元. (三)归纳整理,发展思维函数应用题的一般解题步骤(1)审题: 认真读题,正确理解题意,理顺数量 关系;
(2)建模:合理选取变量,建立实际问题中的变量 之间的函数关系,从而将实际问题转 化为函数模型问题;
(3)解模:运用有关数学知识,解决这个函数模型;
(4)还原:将所得结论转译成实际问题的解答.(四)应用新知,巩固提高巩固练习1
某单位计划用围墙围出一块矩形场地, 现有材料可筑墙的总长度为 l , 如果要使围墙围出的场地面积最大, 问矩形的长、宽各等于多少?(四)应用新知,巩固提高 巩固练习2
某列火车从北京西站开往石家庄, 全程 277 km, 火车出发 10 min 开出 13 km后, 以 120 km/h 匀速行驶. 试写出火车行驶的总路程 S 与匀速行驶的时间 t 之间的关系式, 并求火车离开北京 2 h 内行驶的路程.(五)归纳整理,布置作业小结:知识:一次、二次函数模型在实际中的应用;
步骤:审题、建模、解模、还原;
问题:审题不清,建模错误,忽略定义域和检验
思想:划归思想、函数思想.(五)归纳整理,布置作业作业:必做:教材68页 1,3,4选做:要建一个容积为8 m3,深为2 m 的长方体无盖水池, 如果池底和池壁的造价每平方米分别为 120 元和 80 元, 试求应当怎样设计, 才能使水池总造价最低?并求此最低造价.
