22.1.4二次函数的图象和性质(第一课时)课件
文档属性
| 名称 | 22.1.4二次函数的图象和性质(第一课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 40.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-11 21:15:15 | ||
图片预览



文档简介
课件19张PPT。22.1.4二次函数
图象和性质(第1课时)22.1.4二次函数
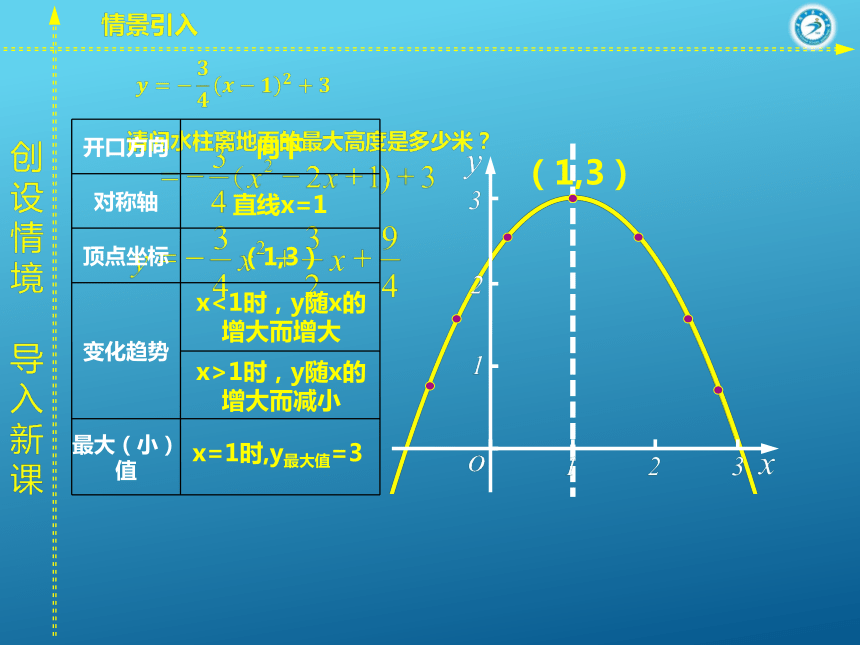
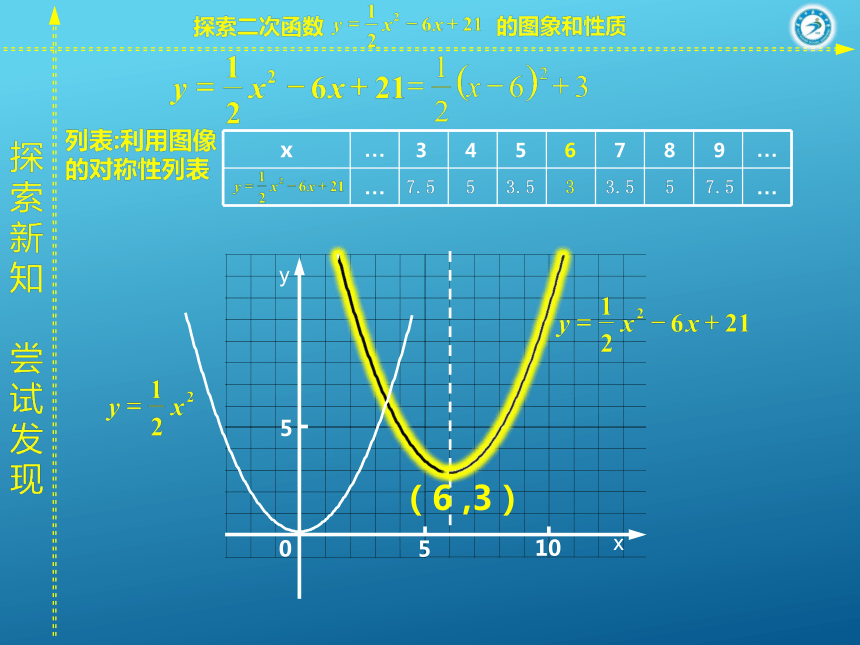
图象和性质(第1课时)(1,3)? 抛物线(1,3)向下直线x=1(1,3)x<1时,y随x的增大而增大x>1时,y随x的增大而减小x=1时,y最大值=3 探索二次函数的图象和性质 如何研究二次函数 的图象和性质?如何将转化成?(6 ,3)(6 ,3)(-1,3)求二次函数y=ax2+bx+c(a≠0)的对称轴和顶点坐标. 配方: 你能写出函数y=ax2+bx+c(a≠0)的顶点吗?探索二次函数的图象和性质?的图象和性质y=ax2+bx+cy=ax2+bx+c(a<0)向上向下(a>0) 写出下列抛物线的开口方向、对称轴
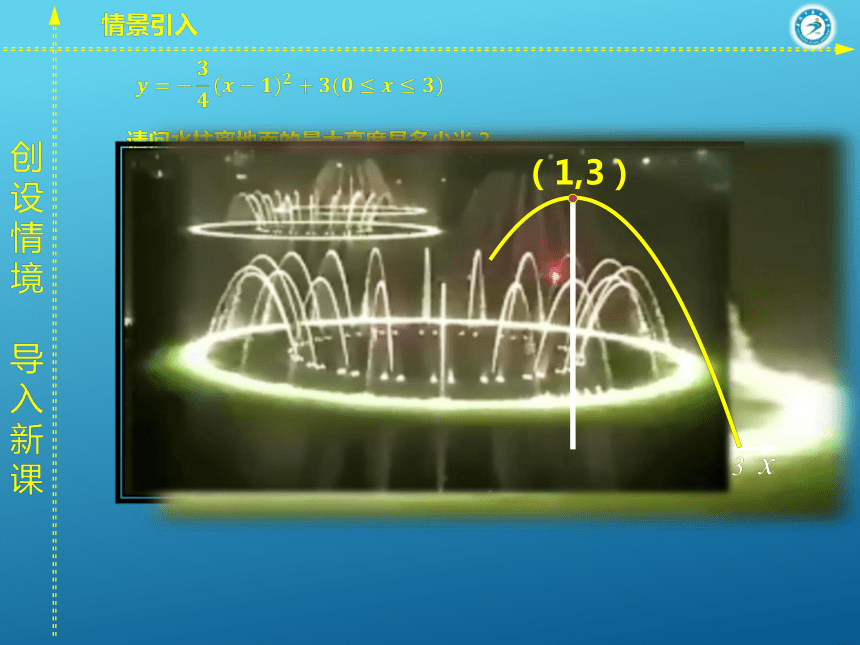
和顶点坐标.巩固训练引例变式则水柱离地面的最大高度是多少米?(1,3)?变式1:?请问水柱水平距离行进多远开始下降?水柱水平行进距离分别是1.6米与2.3米,哪个时刻水柱离地面高一些?(1,3)引例变式变式2:则水柱离地面的最大高度是多少米?变式1:(1,3)引例变式变式3:请问水柱水平距离行进多远开始下降?水柱水平行进距离分别是1.6米与2.3米,哪个时刻水柱离地面高一些?变式2:则水柱离地面的最大高度是多少米?变式1:如果不计其它因素,水池的半径至少要修建多少米,才能使喷出的水流不会落到池外?归纳小结归纳小结配方转化特殊一般?布置作业教科书习题22.1第6、7题.1.已知二次函数 ,用配方法将其化为 的形式为 。2.写出二次函数图象 的开口方向、对称轴和顶点坐标,并画出图象。
3.已知二次函数 ,
当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小。目标检测22.1.4二次函数
图象和性质欢迎指导义务教育课程标准实验教科书九年级 上册
图象和性质(第1课时)22.1.4二次函数
图象和性质(第1课时)(1,3)? 抛物线(1,3)向下直线x=1(1,3)x<1时,y随x的增大而增大x>1时,y随x的增大而减小x=1时,y最大值=3 探索二次函数的图象和性质 如何研究二次函数 的图象和性质?如何将转化成?(6 ,3)(6 ,3)(-1,3)求二次函数y=ax2+bx+c(a≠0)的对称轴和顶点坐标. 配方: 你能写出函数y=ax2+bx+c(a≠0)的顶点吗?探索二次函数的图象和性质?的图象和性质y=ax2+bx+cy=ax2+bx+c(a<0)向上向下(a>0) 写出下列抛物线的开口方向、对称轴
和顶点坐标.巩固训练引例变式则水柱离地面的最大高度是多少米?(1,3)?变式1:?请问水柱水平距离行进多远开始下降?水柱水平行进距离分别是1.6米与2.3米,哪个时刻水柱离地面高一些?(1,3)引例变式变式2:则水柱离地面的最大高度是多少米?变式1:(1,3)引例变式变式3:请问水柱水平距离行进多远开始下降?水柱水平行进距离分别是1.6米与2.3米,哪个时刻水柱离地面高一些?变式2:则水柱离地面的最大高度是多少米?变式1:如果不计其它因素,水池的半径至少要修建多少米,才能使喷出的水流不会落到池外?归纳小结归纳小结配方转化特殊一般?布置作业教科书习题22.1第6、7题.1.已知二次函数 ,用配方法将其化为 的形式为 。2.写出二次函数图象 的开口方向、对称轴和顶点坐标,并画出图象。
3.已知二次函数 ,
当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小。目标检测22.1.4二次函数
图象和性质欢迎指导义务教育课程标准实验教科书九年级 上册
同课章节目录
