22.1.4 二次函数的图象与性质(第二课时)课件
文档属性
| 名称 | 22.1.4 二次函数的图象与性质(第二课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-11 00:00:00 | ||
图片预览







文档简介
课件23张PPT。欢迎各位评委批评指正2018年12月21日星期五在合作中前进
在创新中发展(一) 操 作 方 法人教版义务教育教科书 数学 九年级 上册 §22.1.4
二次函数 的图象和性质
(第2课时)
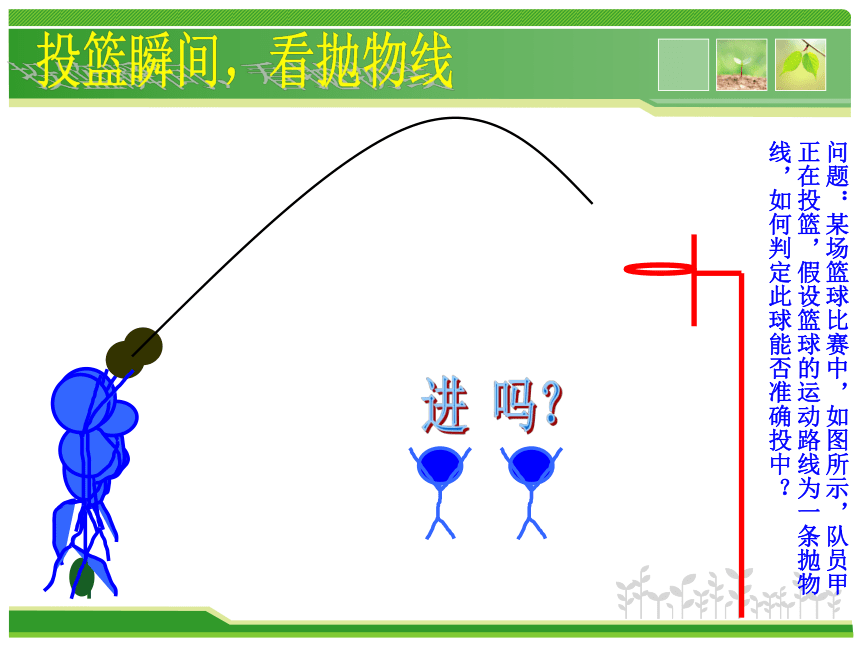
快乐课堂 你我共创投篮瞬间,看抛物线进 吗?投篮瞬间,看抛物线问题:某场篮球比赛中,如图所示,队员甲
正在投篮,假设篮球的运动路线为一条抛物
线,如何判定此球能否准确投中?
2、已知一次函数的图象经过点A(-1,0),B(1,2)求此一次函数的解析式. 问:以上求解析式的方法我们称为_________,它主要的做法是___________________________________
___________________________________________________.解:设一次函数的解析式为y=kx+b待定系数法 ①设函数的解析式;②由条件建立关于待定系数的
方程(组);③解方程(组)从而得到函数解析式;④作答∴所求一次函数为:y=x+1活动二:类比探索,解决问题 1、二次函数y=ax2+bx+c中有几个待定系数?求解析式就是求什么呢?①如果一个二次函数的图象经过(-1,0),能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?②如果一个二次函数的图象经过(-1,0),(1,2)能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.如果不能,请思考为什么?③如果一个二次函数的图象经过(-1,0),(1,2)(3,0)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么? 2、请同们猜想一下,一般由几个点的坐标可以确定二次函数?这几个点应该满足什么条件呢?活动二:类比探索,解决问题①如果一个二次函数的图象经过(-1,0),能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?说明由一个点的坐标不能唯一确定这个二次函数的解析式。活动二:类比探索,解决问题①如果一个二次函数的图象经过(-1,0),能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题②如果一个二次函数的图象经过(-1,0),(1,2)能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.如果不能,请思考为什么?说明由一般的两个点的坐标不能唯一确定这个二次函数的解析式。活动二:类比探索,解决问题②如果一个二次函数的图象经过(-1,0),(1,2)能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.如果不能,请思考为什么?活动二:类比探索,解决问题③如果一个二次函数的图象经过(-1,0),(1,2)(3,0)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题你能说一说用待定系数法求二次函数解析式的一般过程与要求吗?③如果一个二次函数的图象经过(-1,0),(1,2)(3,0)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题 例1:一个二次函数的图象经过(-1,10),(1,4),(2,7)三个点,求这个二次函数的解析式.∴所求二次函数为y=2x2 -3x +5活动二:类比探索,解决问题④如果一个二次函数的图象经过(-1,0),(0,1)(1,2)三点,能确定一个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么? 说明由在同一条直线上的三个点的坐标不能确定这个二次函数的解析式。活动二:类比探索,解决问题④如果一个二次函数的图象经过(-1,0),(0,1)(1,2)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么? 说明由在同一条直线上的三个点的坐标不能唯一确定这个二次函数的解析式。活动二:类比探索,解决问题⑤如果一个二次函数的图象经过(-1,0),(1,2)两个点,其中点(1,2)为此二次函数图象的顶点,能确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题⑤如果一个二次函数的图象经过(-1,0),(1,2)两个点,其中点(1,2)为此二次函数图象的顶点,能确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题进 吗?投篮瞬间,看抛物线问题:某场篮球比赛中,如图所示,队员甲
正在投篮,假设篮球的运动路线为一条抛物
线,如何判定此球能否准确投中?
活动二:类比探索,解决问题进 吗?投篮瞬间,看抛物线问题:某场篮球比赛中,如图所示,队员甲
正在投篮,假设篮球的运动路线为一条抛物
线,如何判定此球能否准确投中?
好 球! 经过本节课的探究学习你有什么收获,感受到了哪些数学思想与方法,还有哪些疑问? 1、用待定系数法求二次函数的一般步骤,设——列——解——答。 2、能求出二次函数解析式一般的三个点的坐标应满足的条件。不在同一条直线上的三个点(或任意两点的连线不与y轴平行的三个点)的坐标。3、经历了猜想——验证——得出结论的过程。4、用方程(组)去解决问题,即方程思想。 6、验证确定二次函数的解析式一般需要几个点时既可从数的方面,也可从形的方面,即数形结合思想。 5、求二次函数的解析式的方法是通过与求一次函数解析式的方法类比得到,即类比思想。活动三:归纳总结,升华认知2、在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=900,AO=BO,点A的坐标为(-3,1)
(1)求点B的坐标;
(2)求以A为顶点,且经过B点的抛物线的解析式 .活动四:课后练习,巩固知识感谢专家们的指点谢谢评委们的聆听
在创新中发展(一) 操 作 方 法人教版义务教育教科书 数学 九年级 上册 §22.1.4
二次函数 的图象和性质
(第2课时)
快乐课堂 你我共创投篮瞬间,看抛物线进 吗?投篮瞬间,看抛物线问题:某场篮球比赛中,如图所示,队员甲
正在投篮,假设篮球的运动路线为一条抛物
线,如何判定此球能否准确投中?
2、已知一次函数的图象经过点A(-1,0),B(1,2)求此一次函数的解析式. 问:以上求解析式的方法我们称为_________,它主要的做法是___________________________________
___________________________________________________.解:设一次函数的解析式为y=kx+b待定系数法 ①设函数的解析式;②由条件建立关于待定系数的
方程(组);③解方程(组)从而得到函数解析式;④作答∴所求一次函数为:y=x+1活动二:类比探索,解决问题 1、二次函数y=ax2+bx+c中有几个待定系数?求解析式就是求什么呢?①如果一个二次函数的图象经过(-1,0),能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?②如果一个二次函数的图象经过(-1,0),(1,2)能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.如果不能,请思考为什么?③如果一个二次函数的图象经过(-1,0),(1,2)(3,0)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么? 2、请同们猜想一下,一般由几个点的坐标可以确定二次函数?这几个点应该满足什么条件呢?活动二:类比探索,解决问题①如果一个二次函数的图象经过(-1,0),能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?说明由一个点的坐标不能唯一确定这个二次函数的解析式。活动二:类比探索,解决问题①如果一个二次函数的图象经过(-1,0),能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题②如果一个二次函数的图象经过(-1,0),(1,2)能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.如果不能,请思考为什么?说明由一般的两个点的坐标不能唯一确定这个二次函数的解析式。活动二:类比探索,解决问题②如果一个二次函数的图象经过(-1,0),(1,2)能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.如果不能,请思考为什么?活动二:类比探索,解决问题③如果一个二次函数的图象经过(-1,0),(1,2)(3,0)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题你能说一说用待定系数法求二次函数解析式的一般过程与要求吗?③如果一个二次函数的图象经过(-1,0),(1,2)(3,0)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题 例1:一个二次函数的图象经过(-1,10),(1,4),(2,7)三个点,求这个二次函数的解析式.∴所求二次函数为y=2x2 -3x +5活动二:类比探索,解决问题④如果一个二次函数的图象经过(-1,0),(0,1)(1,2)三点,能确定一个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么? 说明由在同一条直线上的三个点的坐标不能确定这个二次函数的解析式。活动二:类比探索,解决问题④如果一个二次函数的图象经过(-1,0),(0,1)(1,2)三点,能唯一确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么? 说明由在同一条直线上的三个点的坐标不能唯一确定这个二次函数的解析式。活动二:类比探索,解决问题⑤如果一个二次函数的图象经过(-1,0),(1,2)两个点,其中点(1,2)为此二次函数图象的顶点,能确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题⑤如果一个二次函数的图象经过(-1,0),(1,2)两个点,其中点(1,2)为此二次函数图象的顶点,能确定这个二次函数的解析式吗?如果能,求出这个二次函数的解析式。如果不能,请思考为什么?活动二:类比探索,解决问题进 吗?投篮瞬间,看抛物线问题:某场篮球比赛中,如图所示,队员甲
正在投篮,假设篮球的运动路线为一条抛物
线,如何判定此球能否准确投中?
活动二:类比探索,解决问题进 吗?投篮瞬间,看抛物线问题:某场篮球比赛中,如图所示,队员甲
正在投篮,假设篮球的运动路线为一条抛物
线,如何判定此球能否准确投中?
好 球! 经过本节课的探究学习你有什么收获,感受到了哪些数学思想与方法,还有哪些疑问? 1、用待定系数法求二次函数的一般步骤,设——列——解——答。 2、能求出二次函数解析式一般的三个点的坐标应满足的条件。不在同一条直线上的三个点(或任意两点的连线不与y轴平行的三个点)的坐标。3、经历了猜想——验证——得出结论的过程。4、用方程(组)去解决问题,即方程思想。 6、验证确定二次函数的解析式一般需要几个点时既可从数的方面,也可从形的方面,即数形结合思想。 5、求二次函数的解析式的方法是通过与求一次函数解析式的方法类比得到,即类比思想。活动三:归纳总结,升华认知2、在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=900,AO=BO,点A的坐标为(-3,1)
(1)求点B的坐标;
(2)求以A为顶点,且经过B点的抛物线的解析式 .活动四:课后练习,巩固知识感谢专家们的指点谢谢评委们的聆听
同课章节目录
