4.1.1 指数(第一课时课件)-高一数学同步备课(人教A版2019必修第一册)(共30张PPT)
文档属性
| 名称 | 4.1.1 指数(第一课时课件)-高一数学同步备课(人教A版2019必修第一册)(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 738.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 14:17:25 | ||
图片预览










文档简介
(共30张PPT)
第四章 指数函数与对数函数
4.1.1 n次方根与分数指数幂
高中数学/人教A版/必修一
……
在某一适宜的环境下,某种细菌每2小时分裂一次,从一个细菌开始分裂,一个分裂成两个,经过t小时后,细菌数y为多少?
y = (t>0)
思考:这里细胞数y是时间t的函数吗?
类似地,(±2)4=16,则±2叫做16的 4次方根 ;
25=32,则2叫做32的 5次方根 .
① (±2)2=4,则称±2为4的 平方根 ;
② 23=8,则称2为8的 立方根 ;
1
n次方根的概念
一般地,如果xn=a,那么x叫做a的 ,
其中n>1,且n∈N﹡.
n次方根
-2
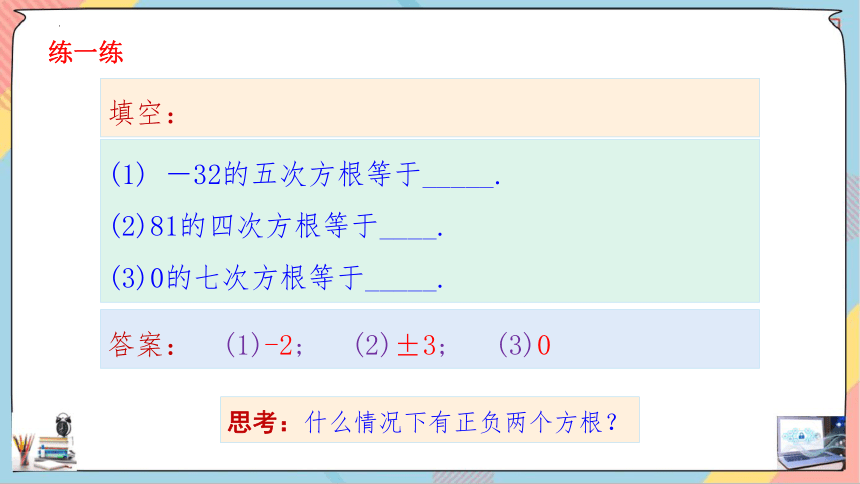
(1) -32的五次方根等于_____.
(2)81的四次方根等于____.
(3)0的七次方根等于_____.
练一练
填空:
答案: (1)-2; (2)±3; (3)0
思考:什么情况下有正负两个方根?
正数的奇次方根是一个正数;
负数的奇次方根是一个负数;
0的奇次方根是0.
2
n次方根的性质
奇次方根:
正数的偶次方根有两个,且互为相反数;
负数没有偶次方根;
0的偶次方根是0.
偶次方根:
0的任何次方根都是0,记作 =0.
当n为奇数时,
当n为偶数时,
3
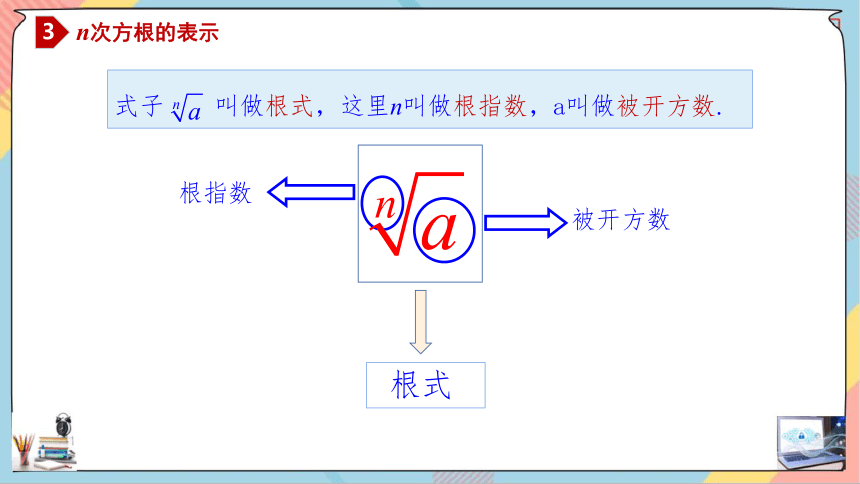
n次方根的表示
式子 叫做根式,这里n叫做根指数,a叫做被开方数.
根指数
被开方数
3
n次方根的表示
根式
结论: .
1.根据方根的意义确定下面式子的值:
练一练
(1)= ;
(2)= ;
(3)= .
a
2.填空:
(1)= ; (2)= .
结论:当n为奇数时, =
a
3.填空:
(1)= ; (2)= .
(3)= ; (4)= .
结论:当n为偶数时, =
4
整数幂的方根
⑴当n为任意正整数时,( )n = a .
⑵当n为奇数时, =a;
当n为偶数时, =|a|= .
对比与小结
(1) ; (2) ;
(3) ; (4) (a>b)
答案:(1) -8 (2) 10
(3) π-3 (4) a - b
练一练
求下列各式的值:
5
分数指数幂
= = a2 = (a>0)
= = a3 = (a>0)
= (a>0)
= (b>0)
= (c>0)
5
分数指数幂
我们规定,正数的正分数指数幂的意义是
(a>0, m、n∈N且n>1)
我们规定,正数的负分数指数幂的意义是
(a>0, m、n∈N且n>1)
0的正分数指数幂等于0,0的负分数指数幂没有意义.
把下列的分数指数式化为根式,把根式化成分数指数式.
;
;
练一练
(1)= ; (2)= ;
(3)= ; (4)= .
答案:(1) ; (2) ;
(3) ; (4) .
解决根式的化简或求值问题,首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简或求值.
有理数指数幂的性质:
6
有理数指数幂的运算性质
例1. 用分数指数幂的形式表示下列各式(a>0):
解析:
(1) ; (2) ;
(3) .
练一练
用分数指数幂表示下列各式:
答案:(1) ; (2) ; (3) .
解析:
方法总结:注意把数转化成乘方的形式.
例2. 求值:(1) ; (2);
(3)( ; (4)(
练一练
(1)= ; (2)
(3) (4)
1.求值:
答案:(1)8 ; (2) ;
(3) ; (4) 2 .
练一练
2.计算:=( )
A.x B.-x
C.-x D.x
答案:C
解析:
(1) ;
(2) .
例3. 计算下列各式(式中字母都是正数):
解析:
解:
练一练
计算下列各式的值:
综合练习
计算下列各式的值:
解析:(1)原式=
计算下列各式的值:
综合练习
解析:(2)原式=
计算下列各式的值:
综合练习
课堂小结
一、本节课学习的新知识
n次方根的概念
n次方根的性质
n次方根的表示
整数幂的方根
分数指数幂
有理数指数幂的运算性质
二、本节课提升的核心素养
数学抽象
直观想象
课堂小结
数学运算
三、本节课训练的数学思想方法
类比联想
课堂小结
分类讨论
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
给授课教师的建议:
1. 素养篇与思维篇中的问题,建议以学生分析为主,由
学生思考、探究、讨论,得出解决方案,教师适时点
拨即可;
2. 原PPT上的“分析”文本框内容,仅供教师参考,上
课前建议删除,使问题解决的过程得以原生态呈现.
(本页可以删了!)
第四章 指数函数与对数函数
4.1.1 n次方根与分数指数幂
高中数学/人教A版/必修一
……
在某一适宜的环境下,某种细菌每2小时分裂一次,从一个细菌开始分裂,一个分裂成两个,经过t小时后,细菌数y为多少?
y = (t>0)
思考:这里细胞数y是时间t的函数吗?
类似地,(±2)4=16,则±2叫做16的 4次方根 ;
25=32,则2叫做32的 5次方根 .
① (±2)2=4,则称±2为4的 平方根 ;
② 23=8,则称2为8的 立方根 ;
1
n次方根的概念
一般地,如果xn=a,那么x叫做a的 ,
其中n>1,且n∈N﹡.
n次方根
-2
(1) -32的五次方根等于_____.
(2)81的四次方根等于____.
(3)0的七次方根等于_____.
练一练
填空:
答案: (1)-2; (2)±3; (3)0
思考:什么情况下有正负两个方根?
正数的奇次方根是一个正数;
负数的奇次方根是一个负数;
0的奇次方根是0.
2
n次方根的性质
奇次方根:
正数的偶次方根有两个,且互为相反数;
负数没有偶次方根;
0的偶次方根是0.
偶次方根:
0的任何次方根都是0,记作 =0.
当n为奇数时,
当n为偶数时,
3
n次方根的表示
式子 叫做根式,这里n叫做根指数,a叫做被开方数.
根指数
被开方数
3
n次方根的表示
根式
结论: .
1.根据方根的意义确定下面式子的值:
练一练
(1)= ;
(2)= ;
(3)= .
a
2.填空:
(1)= ; (2)= .
结论:当n为奇数时, =
a
3.填空:
(1)= ; (2)= .
(3)= ; (4)= .
结论:当n为偶数时, =
4
整数幂的方根
⑴当n为任意正整数时,( )n = a .
⑵当n为奇数时, =a;
当n为偶数时, =|a|= .
对比与小结
(1) ; (2) ;
(3) ; (4) (a>b)
答案:(1) -8 (2) 10
(3) π-3 (4) a - b
练一练
求下列各式的值:
5
分数指数幂
= = a2 = (a>0)
= = a3 = (a>0)
= (a>0)
= (b>0)
= (c>0)
5
分数指数幂
我们规定,正数的正分数指数幂的意义是
(a>0, m、n∈N且n>1)
我们规定,正数的负分数指数幂的意义是
(a>0, m、n∈N且n>1)
0的正分数指数幂等于0,0的负分数指数幂没有意义.
把下列的分数指数式化为根式,把根式化成分数指数式.
;
;
练一练
(1)= ; (2)= ;
(3)= ; (4)= .
答案:(1) ; (2) ;
(3) ; (4) .
解决根式的化简或求值问题,首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简或求值.
有理数指数幂的性质:
6
有理数指数幂的运算性质
例1. 用分数指数幂的形式表示下列各式(a>0):
解析:
(1) ; (2) ;
(3) .
练一练
用分数指数幂表示下列各式:
答案:(1) ; (2) ; (3) .
解析:
方法总结:注意把数转化成乘方的形式.
例2. 求值:(1) ; (2);
(3)( ; (4)(
练一练
(1)= ; (2)
(3) (4)
1.求值:
答案:(1)8 ; (2) ;
(3) ; (4) 2 .
练一练
2.计算:=( )
A.x B.-x
C.-x D.x
答案:C
解析:
(1) ;
(2) .
例3. 计算下列各式(式中字母都是正数):
解析:
解:
练一练
计算下列各式的值:
综合练习
计算下列各式的值:
解析:(1)原式=
计算下列各式的值:
综合练习
解析:(2)原式=
计算下列各式的值:
综合练习
课堂小结
一、本节课学习的新知识
n次方根的概念
n次方根的性质
n次方根的表示
整数幂的方根
分数指数幂
有理数指数幂的运算性质
二、本节课提升的核心素养
数学抽象
直观想象
课堂小结
数学运算
三、本节课训练的数学思想方法
类比联想
课堂小结
分类讨论
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
给授课教师的建议:
1. 素养篇与思维篇中的问题,建议以学生分析为主,由
学生思考、探究、讨论,得出解决方案,教师适时点
拨即可;
2. 原PPT上的“分析”文本框内容,仅供教师参考,上
课前建议删除,使问题解决的过程得以原生态呈现.
(本页可以删了!)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
