幂函数(山东省济南市)
图片预览




文档简介
课件10张PPT。幂函数济南第十一中学数学组 马可宇 ——幂函数的图象及性质观察下列函数,它们的共同特征是什么:共同的特征:
自变量都在指数的位置上,底数都是常数。共同的特征:
自变量都在底数的位置上,指数都是常数。幂函数y = 3x
y = (2/3)x
y = 5x
y = 7x复习引入: 幂函数的定义:
一般地,形如
的函数称为幂函数,其中 为常数.注意:
1.幂函数的自变量在底数位置上.
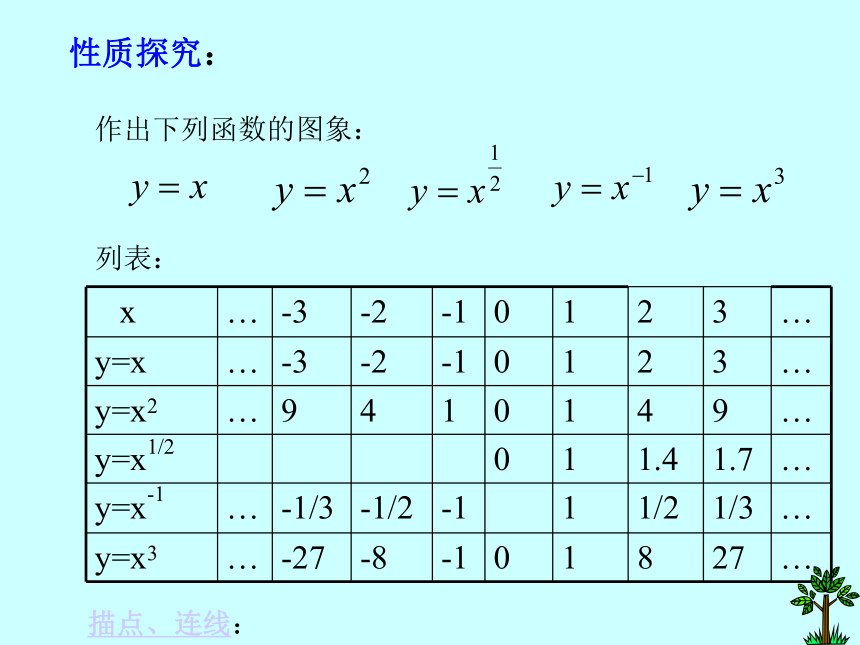
2.幂函数的指数为常数3.幂函数的自变量的系数为 1. 性质探究:作出下列函数的图象:
列表:描点、连线:例1:比较下列两个代数式值的大小:
(1) (a+1) 1.5 , a1.5 (2) (2+a2) -2/3 , 2-2/3(1)考察幂函数 y = x1.5 ,(2)考察幂函数 y = x-2/3,在第一象限内,y的值 随x 的增大而减小。
因为2+a2 >2
所以(2+a2) -2/3 <2-2/3解:在第一象限内,y的值随 x的增大而增大。因为a+1>a,所以 (a+1) 1.5 >a1.5例题讲解:思考总结:
比较两个代数式的值的大小的解题步骤:1.确定可以利用的幂函数.
2.确定底数所在的区间.
3.确定所利用的幂函数在这个区间上的单 调性.
4.利用函数的单调性确定代数式的大小。课堂练习:
p110 习题3-3 B 第1题若a为正偶数
若a为正奇数定义域RR过定点(1,1),(0,0),(-1,1)(1,1),(0,0),(-1,-1)象限第一、二第一、三奇偶性偶函数奇函数在x>0上是增函数,在x< 0上 是减函数.增函数.单调性(图象)(图象)探究讨论:例2:讨论函数 的定义域、奇偶性,作出它的图象。并根据图象说明函数的增减性。解:函数 y=x2/3 ,定义域是实数集R.
因为 f(-x)= (-x)2/3 =[(-x)2]1/3 =(x2)1/3 = x2/3
所以 函数 y=x2/3是偶函数.
因此它的图象关于y轴对称.作出这个函数在[0, )的图象:
列表作图:拓展应用:课堂小结:1.幂函数的定义、图象、性质:2.幂函数的图象的位置和形状的变化:3.利用的数学思想:
数形结合的思想、由特殊到一般的思想.作业:p110 习题3-3 A 第2、4题
谢谢指导
自变量都在指数的位置上,底数都是常数。共同的特征:
自变量都在底数的位置上,指数都是常数。幂函数y = 3x
y = (2/3)x
y = 5x
y = 7x复习引入: 幂函数的定义:
一般地,形如
的函数称为幂函数,其中 为常数.注意:
1.幂函数的自变量在底数位置上.
2.幂函数的指数为常数3.幂函数的自变量的系数为 1. 性质探究:作出下列函数的图象:
列表:描点、连线:例1:比较下列两个代数式值的大小:
(1) (a+1) 1.5 , a1.5 (2) (2+a2) -2/3 , 2-2/3(1)考察幂函数 y = x1.5 ,(2)考察幂函数 y = x-2/3,在第一象限内,y的值 随x 的增大而减小。
因为2+a2 >2
所以(2+a2) -2/3 <2-2/3解:在第一象限内,y的值随 x的增大而增大。因为a+1>a,所以 (a+1) 1.5 >a1.5例题讲解:思考总结:
比较两个代数式的值的大小的解题步骤:1.确定可以利用的幂函数.
2.确定底数所在的区间.
3.确定所利用的幂函数在这个区间上的单 调性.
4.利用函数的单调性确定代数式的大小。课堂练习:
p110 习题3-3 B 第1题若a为正偶数
若a为正奇数定义域RR过定点(1,1),(0,0),(-1,1)(1,1),(0,0),(-1,-1)象限第一、二第一、三奇偶性偶函数奇函数在x>0上是增函数,在x< 0上 是减函数.增函数.单调性(图象)(图象)探究讨论:例2:讨论函数 的定义域、奇偶性,作出它的图象。并根据图象说明函数的增减性。解:函数 y=x2/3 ,定义域是实数集R.
因为 f(-x)= (-x)2/3 =[(-x)2]1/3 =(x2)1/3 = x2/3
所以 函数 y=x2/3是偶函数.
因此它的图象关于y轴对称.作出这个函数在[0, )的图象:
列表作图:拓展应用:课堂小结:1.幂函数的定义、图象、性质:2.幂函数的图象的位置和形状的变化:3.利用的数学思想:
数形结合的思想、由特殊到一般的思想.作业:p110 习题3-3 A 第2、4题
谢谢指导
