24.1.4《圆周角》(第2课时)说课课件
文档属性
| 名称 | 24.1.4《圆周角》(第2课时)说课课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 675.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-13 00:00:00 | ||
图片预览



文档简介
课件14张PPT。九年级 上册24.1.4 圆周角(第2课时)陈华荣枝江市顾家店中学义务教育课程标准实验教科书(一)创设情境? 导入新课兴趣是最好的老师。首先,根据学生好奇心的特点,利用世界十大未解决的奥秘之一--------麦田怪圈引入,由麦田怪圈抽象出几何图形,观察几何图形的共同特征。
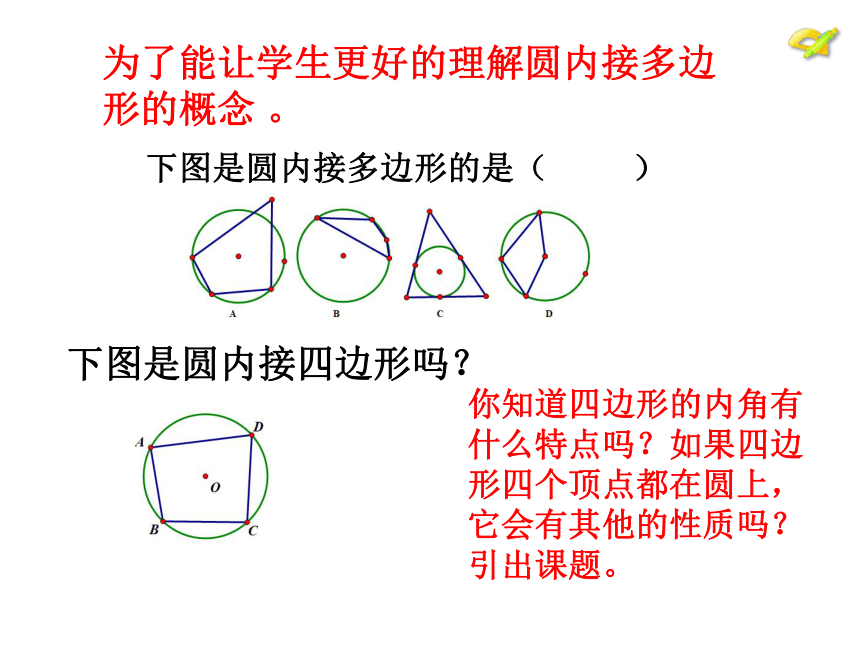
问题一提出,学生的积极性立刻被调动起来,很快就得出圆内接多边形的概念。利用类比的数学方法得出圆内接四边形的定义,引出课题。下图是圆内接四边形吗?下图是圆内接多边形的是( )为了能让学生更好的理解圆内接多边形的概念 。你知道四边形的内角有什么特点吗?如果四边形四个顶点都在圆上,它会有其他的性质吗?引出课题。1、请画出圆O的一个内接四边形。
2、 ∠A、∠B、∠C、∠D是圆周角吗?哪你还记得圆周角定理吗?你能找出∠A、∠B、∠C、∠D分别所对弧吗?
3、用量角器量出∠A、∠C的度数,你能猜想∠A与∠C有什么数量关系?
4、你能用文字语言把你的猜想叙述出来吗?
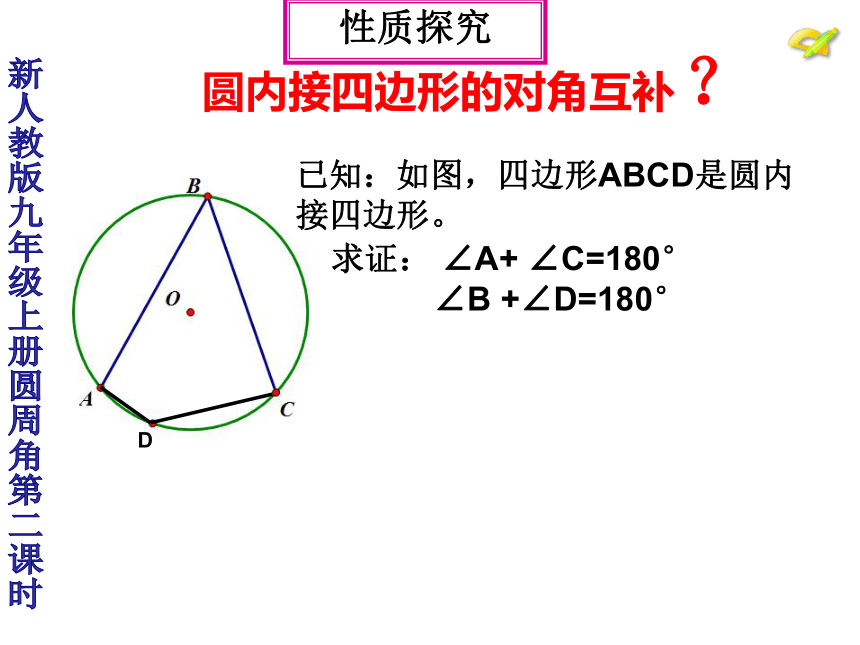
探究新知新人教版九年级上册圆周角第二课时D圆内接四边形的对角互补?已知:如图,四边形ABCD是圆内接四边形。求证: ∠A+ ∠C=180°
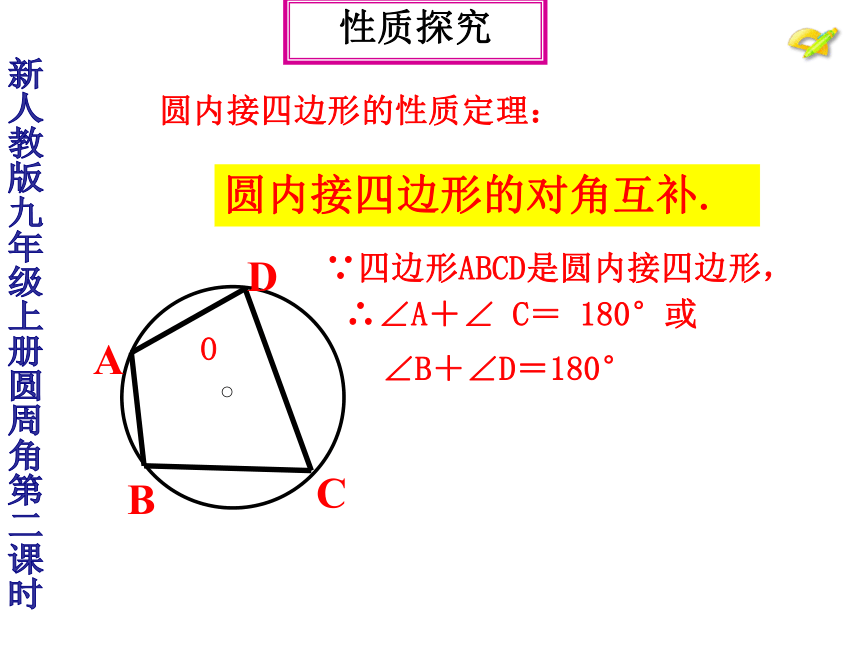
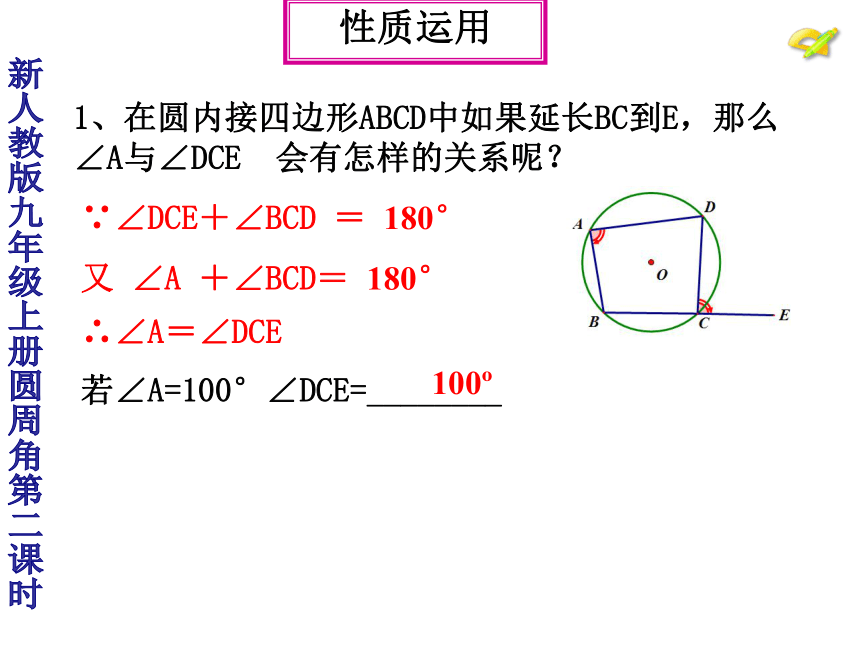
∠B +∠D=180°新人教版九年级上册圆周角第二课时性质探究O∵四边形ABCD是圆内接四边形,∴∠A+∠ C= 180°或∠B+∠D=180°圆内接四边形的对角互补.圆内接四边形的性质定理:新人教版九年级上册圆周角第二课时性质探究1、在圆内接四边形ABCD中如果延长BC到E,那么∠A与∠DCE 会有怎样的关系呢?∵∠DCE+∠BCD = 180°
又 ∠A +∠BCD= 180°
∴∠A=∠DCE性质运用新人教版九年级上册圆周角第二课时若∠A=100°∠DCE=________100o2、如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A、115° B、130°
C、65° D、50°
3、如图,等边三角形ABC内接于⊙O,P是弧AB上的 一点,则∠APB= 。
A120°新人教版九年级上册圆周角第二课时性质运用150o新人教版九年级上册圆周角第二课时圆内接平行四边形是_____________.正方形矩形圆内接菱形是_______________快乐大挑快乐大挑战战60°30°圆内接梯形是______________!等腰梯形602如图,AD、BE 是△ABC 的两条高.
求证:∠CED=∠ABC.1 如图:AB是半圆O的直径,E、D是弧AB上两点,连接AE、BD并延长交与点C。求证: ∠CED=∠ABC大显身手OO新人教版九年级上册圆周角第二课时课堂小结这节课你有什么收获和体会,和大家一起分享一下吧!数学知识数学方法圆内接多边形定义
圆内接四边形的性质类比
实验
猜想
观察
分析
归纳新人教版九年级上册圆周角第二课时六、评价分析本节课整个教学活动从学生的认知规律出发,突出了数学课堂教学中的探索性 。关于圆的内接四边形性质的引出 , 在本教学案例上没有像教材那样直接给出定理,然后证明。而是让学生通过对直观图形的观察归纳和猜想 ,自己去发现结论,并用命题的形式表述结论。关于圆内接四边形性质的证明, 没有采用教师给学生演示定理证明,而是引导学生证明猜想,并做了进一步的完善。这样既调动了学生学习数学的积极性和主动性,增强了学生参与数学活动的意识,又培养了学生的动手实践能力。 本节课充分发挥教师的主导作用和学生的主体作用。教师合理设计使用多媒体,增大课堂容量,提高课堂效率,有效地突出重点,突破难点,使教学过程轻松自如,学生易于并乐于接受,体现了数学教学的时代感。让学生在民主和谐的课堂氛围中探索知识,感受数学创造的乐趣;提高能力,体验获得成功的喜悦。从而更为全面地理解数学,获得更大的发展。 谢 谢
问题一提出,学生的积极性立刻被调动起来,很快就得出圆内接多边形的概念。利用类比的数学方法得出圆内接四边形的定义,引出课题。下图是圆内接四边形吗?下图是圆内接多边形的是( )为了能让学生更好的理解圆内接多边形的概念 。你知道四边形的内角有什么特点吗?如果四边形四个顶点都在圆上,它会有其他的性质吗?引出课题。1、请画出圆O的一个内接四边形。
2、 ∠A、∠B、∠C、∠D是圆周角吗?哪你还记得圆周角定理吗?你能找出∠A、∠B、∠C、∠D分别所对弧吗?
3、用量角器量出∠A、∠C的度数,你能猜想∠A与∠C有什么数量关系?
4、你能用文字语言把你的猜想叙述出来吗?
探究新知新人教版九年级上册圆周角第二课时D圆内接四边形的对角互补?已知:如图,四边形ABCD是圆内接四边形。求证: ∠A+ ∠C=180°
∠B +∠D=180°新人教版九年级上册圆周角第二课时性质探究O∵四边形ABCD是圆内接四边形,∴∠A+∠ C= 180°或∠B+∠D=180°圆内接四边形的对角互补.圆内接四边形的性质定理:新人教版九年级上册圆周角第二课时性质探究1、在圆内接四边形ABCD中如果延长BC到E,那么∠A与∠DCE 会有怎样的关系呢?∵∠DCE+∠BCD = 180°
又 ∠A +∠BCD= 180°
∴∠A=∠DCE性质运用新人教版九年级上册圆周角第二课时若∠A=100°∠DCE=________100o2、如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A、115° B、130°
C、65° D、50°
3、如图,等边三角形ABC内接于⊙O,P是弧AB上的 一点,则∠APB= 。
A120°新人教版九年级上册圆周角第二课时性质运用150o新人教版九年级上册圆周角第二课时圆内接平行四边形是_____________.正方形矩形圆内接菱形是_______________快乐大挑快乐大挑战战60°30°圆内接梯形是______________!等腰梯形602如图,AD、BE 是△ABC 的两条高.
求证:∠CED=∠ABC.1 如图:AB是半圆O的直径,E、D是弧AB上两点,连接AE、BD并延长交与点C。求证: ∠CED=∠ABC大显身手OO新人教版九年级上册圆周角第二课时课堂小结这节课你有什么收获和体会,和大家一起分享一下吧!数学知识数学方法圆内接多边形定义
圆内接四边形的性质类比
实验
猜想
观察
分析
归纳新人教版九年级上册圆周角第二课时六、评价分析本节课整个教学活动从学生的认知规律出发,突出了数学课堂教学中的探索性 。关于圆的内接四边形性质的引出 , 在本教学案例上没有像教材那样直接给出定理,然后证明。而是让学生通过对直观图形的观察归纳和猜想 ,自己去发现结论,并用命题的形式表述结论。关于圆内接四边形性质的证明, 没有采用教师给学生演示定理证明,而是引导学生证明猜想,并做了进一步的完善。这样既调动了学生学习数学的积极性和主动性,增强了学生参与数学活动的意识,又培养了学生的动手实践能力。 本节课充分发挥教师的主导作用和学生的主体作用。教师合理设计使用多媒体,增大课堂容量,提高课堂效率,有效地突出重点,突破难点,使教学过程轻松自如,学生易于并乐于接受,体现了数学教学的时代感。让学生在民主和谐的课堂氛围中探索知识,感受数学创造的乐趣;提高能力,体验获得成功的喜悦。从而更为全面地理解数学,获得更大的发展。 谢 谢
同课章节目录
