【高效备课】人教版九(上) 21.2 解一元二次方程 21.2.1 配方法 第2课时 配方法 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 21.2 解一元二次方程 21.2.1 配方法 第2课时 配方法 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 368.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:32 | ||
图片预览








文档简介
(共22张PPT)
R·九年级上册
21.2 解一元二次方程
21.2.1 配方法
第2课时 配方法
新课导入
导入课题
请把方程(x+3)2=5化成一般形式。
那么你能将方程x2+6x+4=0转化为(x+m)2=n的形式吗?
这节课我们一起来学习配方法。
学习目标
(1)知道用配方法解一元二次方程的一般步骤,会
用配方法解一元二次方程.
(2)通过配方进一步体会“降次”的转化思想.
推进新课
知识点1
用配方法解一元二次方程
怎样解方程x2+6x+4=0
分析:我们已经会解方程(x+3)2=5. 因为它的左边是含有x的完全平方式,右边是非负数,所以可以直接降次解方程.那么,能否将方程x2+6x+4=0转化为可以直接降次的形式再求解呢?
降次
左边写成
完全平方式
使左边配成x2+2bx+b2的形式
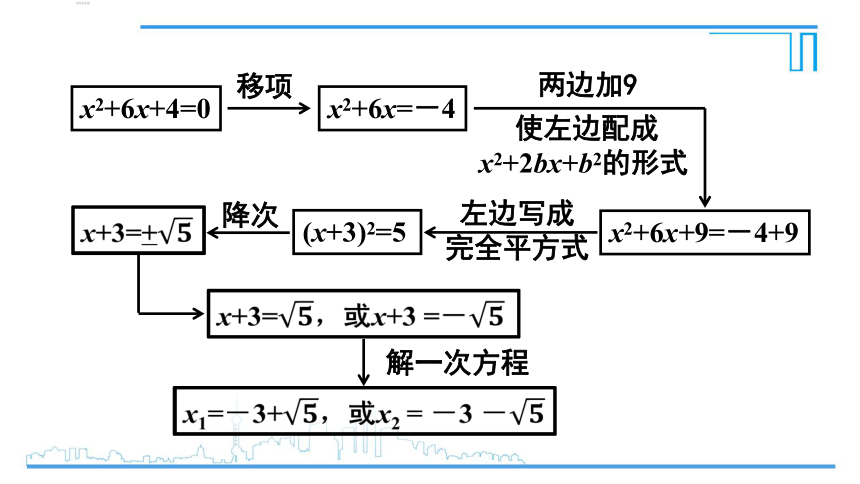
x2+6x+4=0
x2+6x=-4
移项
两边加9
x2+6x+9=-4+9
(x+3)2=5
解一次方程
回忆完全平方公式
a2+2ab+b2=(a+b)2
思考:为什么要在x2+6x=-4两边加9而不是其他数?
因为两边加9,式子左边可以恰好凑成完全平方式.
试一试:对下列各式进行配方:
x2+10x+25
=(x+5)2
x2-12x+36
=(x-6)2
知识点2
用配方法解一元二次方程的一般步骤
例1 解下列方程
(1) x2-8x+1=0 (2)2x2+1=3x (3)3x2-6x+4=0
(1)解:移项,得:x2-8x=-1
配方,得:x2-8x+42=-1+42
(x-4)2=15
(2) 2x2+1=3x
(2) 解:移项,得:2x2-3x=-1
二次项系数化为1:
配方,得:
(3) 3x2-6x+4=0
(3) 解:移项,得:3x2-6x=-4
二次项系数化为1:
配方,得:
因为实数的平方不会是负数,所以x取任何实数时,
(x-1)2都是非负数,上式都不成立,即原方程无实数根.
思考1:用配方法解一元二次方程时,移项时要
注意什么?
思考2:说说配方法解一元二次方程的一般步骤.
移项时需注意改变符号.
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p.
规律总结
①当p>0时,则 ,方程的两个根为
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为
x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
1. 用配方法解方程-x2+6x+7=0时,配方后得的方程为( )
A. (x+3)2=16 B.(x-3)2=16
C.(x+3)2=2 D.(x-3)2=2
2. 填空.
(1) 4x2+4x+1= (2) x2-30x+225=
随堂演练
基础巩固
(2x+1)2
B
(x-15)2
3. 用配方法解下列方程.
(1)x2+10x+9=0; (2)x2+4x-9=2x-11;
解:移项, x2+10x=-9
配方, x2+10x+25=16
(x+5) 2=16
x+5=±4
方程的两个根为
x1=-1,x2=-9
解:移项, x2+2x=-2
配方, x2+2x+1=-1
(x+1)2=-1
方程没有实数根.
(3)x(x+4)=8x+12
解:化简移项 x2-4x=12
配方 x2-4x+4=16
(x-2)2=16
x-2=±4
方程的两个根为x1=6, x2=-2
4. 当a为何值时,多项式a2+2a+18有最小值?并求出
这个最小值.
解:对原式进行配方,则原式=(a+1)2+17
∵(a+1)2≥0,
∴当a=-1时,原式有最小值为17.
25
练习
1. 填空:
【教材P9练习 第1题】
(1)x2+10x +_____ =(x+_____)2
(2)x2 -12x +_____ =(x - _____)2(3)x2+5x +_____ =(x+_____)2
(4)x2 - x +_____ =(x - _____)2
5
36
6
2. 解下列方程。
【教材P9练习 第1题】
(1)x2+10x +9 = 0 (2)x2 -x - = 0
移项,得 x2+10x =-9
配方,得 x2+10x +52 =-9+52
(x+5)2 =16
由此可得 x+5 =±4
x1= -1 , x2=-9
移项,得 x2 - x =
配方,得x2 - x + 2 = + 2
(x - )2 = 2
由此可得 x- =±
x1= + , x2= -
2. 解下列方程。
【教材P9练习 第1题】
(3)3x2+6x -4 = 0 (4)4x2 -6x -3 = 0
移项,得 3x2+6x =4
二次项系数化为1,得 x2+2x =
配方,得 x2+2x +12 = +12
由此可得 x+1 =±
x1= -1+ , x2=-1-
(x +1)2 =
移项,得 4x2 -6x =3
二次项系数化为1,得 x2- x =
配方,得 x2- x + 2 = + 2
由此可得 x- =±
x1= , x2=
(x- )2 =
2. 解下列方程。
【教材P9练习 第1题】
(5)x2+4x-9 = 2x-11 (6)x(x +4) = 8x+12
x2+4x-2x = -11+9
x2+2x = -2
x2+2x +12 = -2+12
原方程无实数根.
(x +1)2 =-1
x2 +4x = 8x+12
x2 -4x = 12
x2 -4x+22 = 12 +22
x-2 =±4
x1= 6, x2= -2
(x-2)2 = 16
课堂小结
配方法解一元二次方程
配方法
直接开平方法
ax2+bx+c=0 (a≠0)
(x+m)2=n (n≥0)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
R·九年级上册
21.2 解一元二次方程
21.2.1 配方法
第2课时 配方法
新课导入
导入课题
请把方程(x+3)2=5化成一般形式。
那么你能将方程x2+6x+4=0转化为(x+m)2=n的形式吗?
这节课我们一起来学习配方法。
学习目标
(1)知道用配方法解一元二次方程的一般步骤,会
用配方法解一元二次方程.
(2)通过配方进一步体会“降次”的转化思想.
推进新课
知识点1
用配方法解一元二次方程
怎样解方程x2+6x+4=0
分析:我们已经会解方程(x+3)2=5. 因为它的左边是含有x的完全平方式,右边是非负数,所以可以直接降次解方程.那么,能否将方程x2+6x+4=0转化为可以直接降次的形式再求解呢?
降次
左边写成
完全平方式
使左边配成x2+2bx+b2的形式
x2+6x+4=0
x2+6x=-4
移项
两边加9
x2+6x+9=-4+9
(x+3)2=5
解一次方程
回忆完全平方公式
a2+2ab+b2=(a+b)2
思考:为什么要在x2+6x=-4两边加9而不是其他数?
因为两边加9,式子左边可以恰好凑成完全平方式.
试一试:对下列各式进行配方:
x2+10x+25
=(x+5)2
x2-12x+36
=(x-6)2
知识点2
用配方法解一元二次方程的一般步骤
例1 解下列方程
(1) x2-8x+1=0 (2)2x2+1=3x (3)3x2-6x+4=0
(1)解:移项,得:x2-8x=-1
配方,得:x2-8x+42=-1+42
(x-4)2=15
(2) 2x2+1=3x
(2) 解:移项,得:2x2-3x=-1
二次项系数化为1:
配方,得:
(3) 3x2-6x+4=0
(3) 解:移项,得:3x2-6x=-4
二次项系数化为1:
配方,得:
因为实数的平方不会是负数,所以x取任何实数时,
(x-1)2都是非负数,上式都不成立,即原方程无实数根.
思考1:用配方法解一元二次方程时,移项时要
注意什么?
思考2:说说配方法解一元二次方程的一般步骤.
移项时需注意改变符号.
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p.
规律总结
①当p>0时,则 ,方程的两个根为
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为
x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
1. 用配方法解方程-x2+6x+7=0时,配方后得的方程为( )
A. (x+3)2=16 B.(x-3)2=16
C.(x+3)2=2 D.(x-3)2=2
2. 填空.
(1) 4x2+4x+1= (2) x2-30x+225=
随堂演练
基础巩固
(2x+1)2
B
(x-15)2
3. 用配方法解下列方程.
(1)x2+10x+9=0; (2)x2+4x-9=2x-11;
解:移项, x2+10x=-9
配方, x2+10x+25=16
(x+5) 2=16
x+5=±4
方程的两个根为
x1=-1,x2=-9
解:移项, x2+2x=-2
配方, x2+2x+1=-1
(x+1)2=-1
方程没有实数根.
(3)x(x+4)=8x+12
解:化简移项 x2-4x=12
配方 x2-4x+4=16
(x-2)2=16
x-2=±4
方程的两个根为x1=6, x2=-2
4. 当a为何值时,多项式a2+2a+18有最小值?并求出
这个最小值.
解:对原式进行配方,则原式=(a+1)2+17
∵(a+1)2≥0,
∴当a=-1时,原式有最小值为17.
25
练习
1. 填空:
【教材P9练习 第1题】
(1)x2+10x +_____ =(x+_____)2
(2)x2 -12x +_____ =(x - _____)2(3)x2+5x +_____ =(x+_____)2
(4)x2 - x +_____ =(x - _____)2
5
36
6
2. 解下列方程。
【教材P9练习 第1题】
(1)x2+10x +9 = 0 (2)x2 -x - = 0
移项,得 x2+10x =-9
配方,得 x2+10x +52 =-9+52
(x+5)2 =16
由此可得 x+5 =±4
x1= -1 , x2=-9
移项,得 x2 - x =
配方,得x2 - x + 2 = + 2
(x - )2 = 2
由此可得 x- =±
x1= + , x2= -
2. 解下列方程。
【教材P9练习 第1题】
(3)3x2+6x -4 = 0 (4)4x2 -6x -3 = 0
移项,得 3x2+6x =4
二次项系数化为1,得 x2+2x =
配方,得 x2+2x +12 = +12
由此可得 x+1 =±
x1= -1+ , x2=-1-
(x +1)2 =
移项,得 4x2 -6x =3
二次项系数化为1,得 x2- x =
配方,得 x2- x + 2 = + 2
由此可得 x- =±
x1= , x2=
(x- )2 =
2. 解下列方程。
【教材P9练习 第1题】
(5)x2+4x-9 = 2x-11 (6)x(x +4) = 8x+12
x2+4x-2x = -11+9
x2+2x = -2
x2+2x +12 = -2+12
原方程无实数根.
(x +1)2 =-1
x2 +4x = 8x+12
x2 -4x = 12
x2 -4x+22 = 12 +22
x-2 =±4
x1= 6, x2= -2
(x-2)2 = 16
课堂小结
配方法解一元二次方程
配方法
直接开平方法
ax2+bx+c=0 (a≠0)
(x+m)2=n (n≥0)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
