【高效备课】人教版九(上) 22.2 二次函数与一元二次方程 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 22.2 二次函数与一元二次方程 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1023.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:32 | ||
图片预览








文档简介
(共25张PPT)
22.2 二次函数与一元二次方程
R·九年级上册
新课导入
导入课题
问题: 以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2.球的飞行高度能否达到15m或20m或20.5m?如能,需要多少飞行时间呢?
(1)知道抛物线y=ax2+bx+c与x轴交点情况与一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的根的情况之间的关系.
(2)会用二次函数的图象求一元二次方程的近似解.
学习目标
推进新课
知识点1
二次函数与一元二次方程的关系
问题 以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2.球的飞行高度能否达到15m或20m或20.5m?如能,需要多少飞行时间呢?
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
h=20t-5t2.
15=20t-5t2.
解:
t2-4t+3=0.
t1=1,
t2=3.
当小球飞行1s和3s时,它的飞行高度为15m.
1s
3s
15m
你能结合图指出为什么在两个时间小球的高度为15m吗?
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
h=20t-5t2.
20=20t-5t2.
解:
t2 - 4t+4=0.
t1 =t2 =2.
当小球飞行2s时,它的飞行高度为20m.
你能结合图指出为什么只在一个时间小球的高度为20m吗?
2s
20m
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
h=20t-5t2.
20.5=20t-5t2.
解:
t2 - 4t+4.1=0.
因为(-4)2 – 4×4.1<0,
所以方程无实根.
2s
20m
即小球的飞行高度不能达到20.5m.
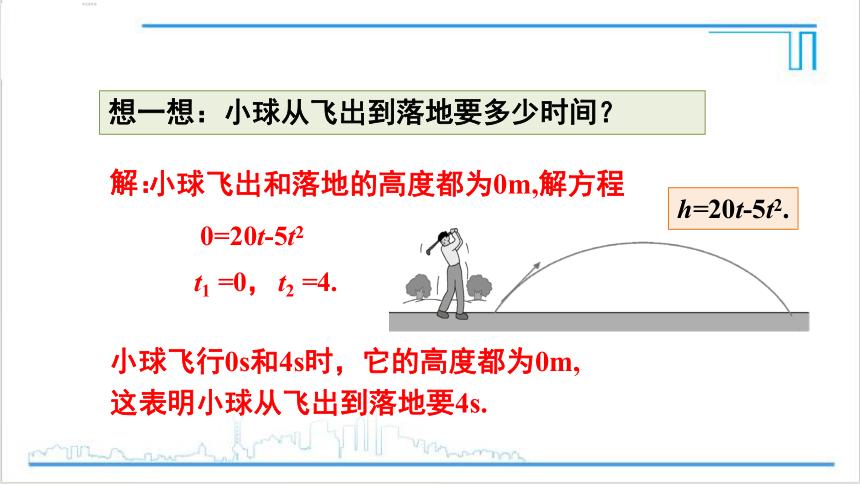
h=20t-5t2.
想一想:小球从飞出到落地要多少时间?
小球飞出和落地的高度都为0m,解方程
0=20t-5t2
t1 =0,
t2 =4.
解:
小球飞行0s和4s时,它的高度都为0m,这表明小球从飞出到落地要4s.
从以上问题的解法中,可以发现:
(1)求y=ax2+bx+c的值为k时的自变量x的值的问题,可以通过解一元二次方程 解决;
(2)求y=ax2+bx+c的值为0时的自变量x的值的问题,可以通过解一元二次方程 解决.
ax2+bx+c=k
ax2+bx+c=0
从上面发现,二次函数y=ax2+bx+c(a≠0)何时为一元二次方程
一般地,当y取定值时,二次函数为一元二次方程.
如:y=5时,则5=ax2+bx+c(a≠0)就是一个一元二次方程.
自由讨论
为一个常数
(定值)
已知二次函数中因变量的值,求自变量的值
解一元二次方程的根
二次函数与一元二次方程的关系(1)
下列二次函数的图象与x轴有公共点吗?若果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
(1)y = x2+x–2 ,(2) y = x2–6x +9 , (3)y = x2 – x+ 1
思考
二次函数图象与x轴的公共点的横坐标是多少?
无公共点
先画出函数图象:
公共点的函数值为 。
0
对应一元二次方程的根是多少?
x1 =-2,
x2 =1.
x1 =x2 =3.
方程无解
有两个不等的实根
有两个相等的实根
没有实数根
由上述问题,你可以得到什么结论呢?
方程ax2+bx+c=0的解就是抛物线y=ax2+bx+c与x轴公共点的横坐标。当抛物线与x轴没有公共点时,对应的方程无实数根.
反过来,由一元
二次方程的根的情
况,也可以确定相
应的二次函数的图
象与 x 轴的位置关
系。
有两个不同实根
有两个相同实根
没有根
有两个交点
有一个交点
没有交点
△ > 0
△ = 0
△ < 0
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系(2)
ax2+bx+c = 0 的根
抛物线 y=ax2+bx+c与x轴
若抛物线 y=ax2+bx+c 与 x 轴有交点,则________________ 。
b2 – 4ac ≥ 0
△= b2 – 4ac
△>0
△=0
△<0
o
x
y
△ = b2 – 4ac
y=ax2+bx+c
那么a<0时呢?
a>0
知识点2
用图象法求一元二次方程的近似解
例 利用函数图象求方程x -2x-2=0的实数解.
解:
作y=x -2x-2的图象,
它与x轴的公共点的横坐标大约是-0.7,2.7
所以方程x -2x-2=0的实数根为x1≈-0.7,x2≈2.7
3
y
O
-3
3
x
先画出函数图象,再通过函数图象找点
3
y
O
-3
3
x
(-0.7,0)
(2.7,0)
你能利用函数图象指出x -2x-2<0和x -2x-2>0的解集吗?
y=x -2x-2
解:x -2x-2<0的解集为-0.7x -2x-2>0的解集为x>2.7或x<-0.7.
随堂演练
基础巩固
1. 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
2.抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),则这条抛物线的对称轴是( )
A.直线x=-1 B.直线x=0 C.直线x=1 D.直线x=3
B
C
3.抛物线y=-2(x+4)(x-2)与x轴的两个交点坐标为 .
4.抛物线y=x2-x-2与直线y=4的交点坐标是 ,与y轴的交点坐标是 .
(-4,0),(2,0)
(-2,4),(3,4)
(0,-2)
5.在图中画出函数y=x2-2x-3的图象,利用图象回答:
(1)方程x2-2x-3=0的解是多少;
(2) x取什么值时,函数值大于0;
(3) x取什么值时,函数值小于0.
解:图象如图所示.
(1) 方程x2-2x-3=0的解为x1=-1,x2=3.
(2) x>3或x<-1时,函数值大于0.
(3) -13
y
O
-3
3
x
综合应用
解:
(1)如图所示.
(2)由图象可知,铅球推出的距离为10.
拓展延伸
7.把下列各题中解析式的编号①②③④与图象的编号A、B、C、D对应起来.
①y=x2+bx+2; ②y=ax(x-3);
③y=a(x+2)(x-3); ④y=-x2+bx-3.
A. ; B. ; C. ; D. .
①
④
③
②
课堂小结
(2)通过画函数的图象解一元二次方程是数的直观化的体现,但存在作图的误差,因此通过这种方法求得的方程的根一般是近似的.
(1)当抛物线的顶点在x轴上,即抛物线与x轴只有一个公共点时,相应的方程有两个相等的实数根,二者不要混淆,对“数”来说是两个,对“形”来说是一个.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
22.2 二次函数与一元二次方程
R·九年级上册
新课导入
导入课题
问题: 以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2.球的飞行高度能否达到15m或20m或20.5m?如能,需要多少飞行时间呢?
(1)知道抛物线y=ax2+bx+c与x轴交点情况与一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的根的情况之间的关系.
(2)会用二次函数的图象求一元二次方程的近似解.
学习目标
推进新课
知识点1
二次函数与一元二次方程的关系
问题 以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2.球的飞行高度能否达到15m或20m或20.5m?如能,需要多少飞行时间呢?
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
h=20t-5t2.
15=20t-5t2.
解:
t2-4t+3=0.
t1=1,
t2=3.
当小球飞行1s和3s时,它的飞行高度为15m.
1s
3s
15m
你能结合图指出为什么在两个时间小球的高度为15m吗?
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
h=20t-5t2.
20=20t-5t2.
解:
t2 - 4t+4=0.
t1 =t2 =2.
当小球飞行2s时,它的飞行高度为20m.
你能结合图指出为什么只在一个时间小球的高度为20m吗?
2s
20m
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
h=20t-5t2.
20.5=20t-5t2.
解:
t2 - 4t+4.1=0.
因为(-4)2 – 4×4.1<0,
所以方程无实根.
2s
20m
即小球的飞行高度不能达到20.5m.
h=20t-5t2.
想一想:小球从飞出到落地要多少时间?
小球飞出和落地的高度都为0m,解方程
0=20t-5t2
t1 =0,
t2 =4.
解:
小球飞行0s和4s时,它的高度都为0m,这表明小球从飞出到落地要4s.
从以上问题的解法中,可以发现:
(1)求y=ax2+bx+c的值为k时的自变量x的值的问题,可以通过解一元二次方程 解决;
(2)求y=ax2+bx+c的值为0时的自变量x的值的问题,可以通过解一元二次方程 解决.
ax2+bx+c=k
ax2+bx+c=0
从上面发现,二次函数y=ax2+bx+c(a≠0)何时为一元二次方程
一般地,当y取定值时,二次函数为一元二次方程.
如:y=5时,则5=ax2+bx+c(a≠0)就是一个一元二次方程.
自由讨论
为一个常数
(定值)
已知二次函数中因变量的值,求自变量的值
解一元二次方程的根
二次函数与一元二次方程的关系(1)
下列二次函数的图象与x轴有公共点吗?若果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
(1)y = x2+x–2 ,(2) y = x2–6x +9 , (3)y = x2 – x+ 1
思考
二次函数图象与x轴的公共点的横坐标是多少?
无公共点
先画出函数图象:
公共点的函数值为 。
0
对应一元二次方程的根是多少?
x1 =-2,
x2 =1.
x1 =x2 =3.
方程无解
有两个不等的实根
有两个相等的实根
没有实数根
由上述问题,你可以得到什么结论呢?
方程ax2+bx+c=0的解就是抛物线y=ax2+bx+c与x轴公共点的横坐标。当抛物线与x轴没有公共点时,对应的方程无实数根.
反过来,由一元
二次方程的根的情
况,也可以确定相
应的二次函数的图
象与 x 轴的位置关
系。
有两个不同实根
有两个相同实根
没有根
有两个交点
有一个交点
没有交点
△ > 0
△ = 0
△ < 0
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系(2)
ax2+bx+c = 0 的根
抛物线 y=ax2+bx+c与x轴
若抛物线 y=ax2+bx+c 与 x 轴有交点,则________________ 。
b2 – 4ac ≥ 0
△= b2 – 4ac
△>0
△=0
△<0
o
x
y
△ = b2 – 4ac
y=ax2+bx+c
那么a<0时呢?
a>0
知识点2
用图象法求一元二次方程的近似解
例 利用函数图象求方程x -2x-2=0的实数解.
解:
作y=x -2x-2的图象,
它与x轴的公共点的横坐标大约是-0.7,2.7
所以方程x -2x-2=0的实数根为x1≈-0.7,x2≈2.7
3
y
O
-3
3
x
先画出函数图象,再通过函数图象找点
3
y
O
-3
3
x
(-0.7,0)
(2.7,0)
你能利用函数图象指出x -2x-2<0和x -2x-2>0的解集吗?
y=x -2x-2
解:x -2x-2<0的解集为-0.7
随堂演练
基础巩固
1. 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
2.抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),则这条抛物线的对称轴是( )
A.直线x=-1 B.直线x=0 C.直线x=1 D.直线x=3
B
C
3.抛物线y=-2(x+4)(x-2)与x轴的两个交点坐标为 .
4.抛物线y=x2-x-2与直线y=4的交点坐标是 ,与y轴的交点坐标是 .
(-4,0),(2,0)
(-2,4),(3,4)
(0,-2)
5.在图中画出函数y=x2-2x-3的图象,利用图象回答:
(1)方程x2-2x-3=0的解是多少;
(2) x取什么值时,函数值大于0;
(3) x取什么值时,函数值小于0.
解:图象如图所示.
(1) 方程x2-2x-3=0的解为x1=-1,x2=3.
(2) x>3或x<-1时,函数值大于0.
(3) -1
y
O
-3
3
x
综合应用
解:
(1)如图所示.
(2)由图象可知,铅球推出的距离为10.
拓展延伸
7.把下列各题中解析式的编号①②③④与图象的编号A、B、C、D对应起来.
①y=x2+bx+2; ②y=ax(x-3);
③y=a(x+2)(x-3); ④y=-x2+bx-3.
A. ; B. ; C. ; D. .
①
④
③
②
课堂小结
(2)通过画函数的图象解一元二次方程是数的直观化的体现,但存在作图的误差,因此通过这种方法求得的方程的根一般是近似的.
(1)当抛物线的顶点在x轴上,即抛物线与x轴只有一个公共点时,相应的方程有两个相等的实数根,二者不要混淆,对“数”来说是两个,对“形”来说是一个.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
