【高效备课】人教版九(上) 22.3 实际问题与二次函数 第3课时 抛物线形问题 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 22.3 实际问题与二次函数 第3课时 抛物线形问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 905.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:32 | ||
图片预览




文档简介
(共15张PPT)
22.3 实际问题与二次函数
第3课时 抛物线形问题
R·九年级上册
新课导入
导入课题
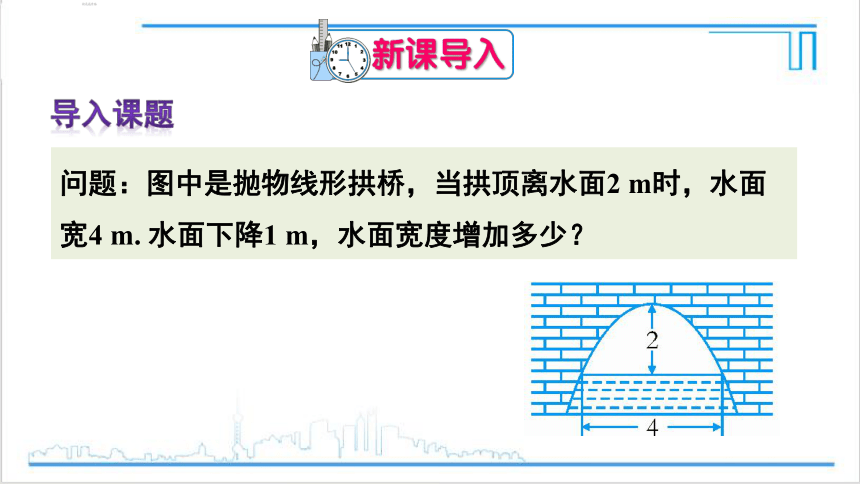
问题:图中是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m. 水面下降1 m,水面宽度增加多少?
(1)能建立合适的直角坐标系,用二次函数的知识解决与抛物线相关的实际问题.
(2)进一步巩固二次函数的性质与图象特征.
学习目标
推进新课
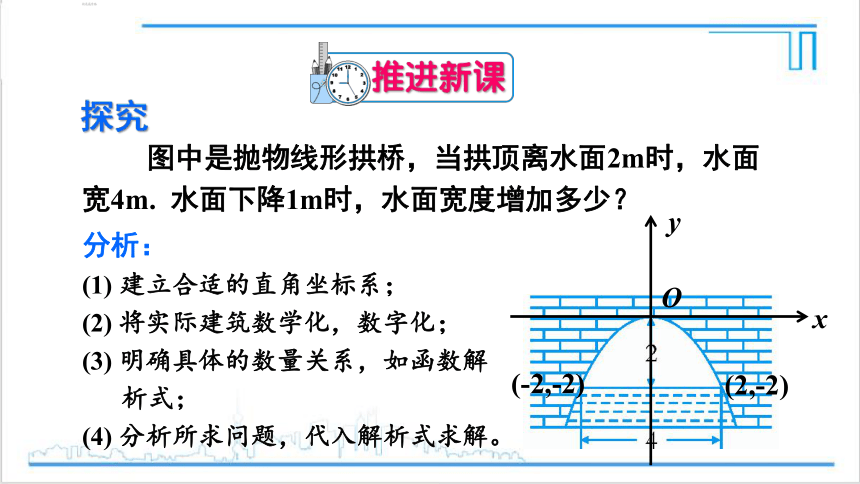
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m. 水面下降1m时,水面宽度增加多少?
分析:
(1) 建立合适的直角坐标系;
(2) 将实际建筑数学化,数字化;
(3) 明确具体的数量关系,如函数解
析式;
(4) 分析所求问题,代入解析式求解。
探究
(2,-2)
(-2,-2)
x
y
O
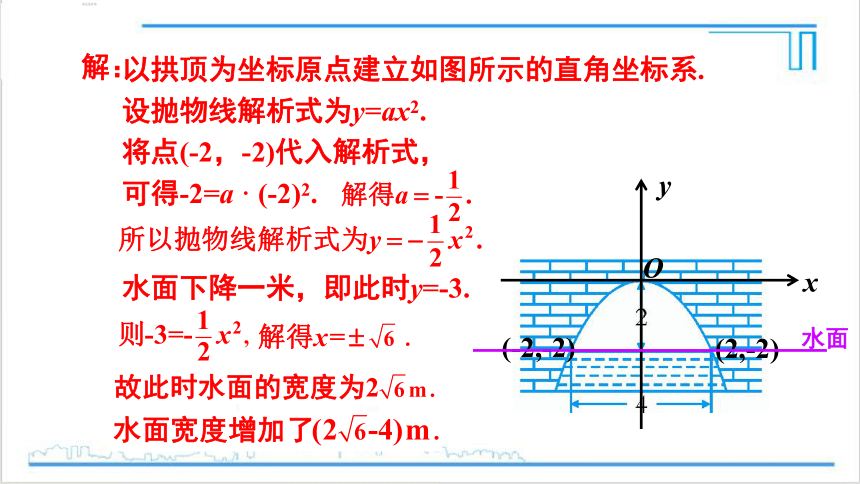
解:
以拱顶为坐标原点建立如图所示的直角坐标系.
设抛物线解析式为y=ax2.
将点(-2,-2)代入解析式,
可得-2=a · (-2)2.
x
y
O
(2,-2)
(-2,-2)
水面
水面下降一米,即此时y=-3.
如果以下降1 m后的水面为x轴,以抛物线的对称轴为y轴,建立直角坐标系. 与前面方法的结果相同吗?
y
O
(2,1)
(-2,1)
水面
x
(0,3)
解:
依题意建立如图所示的直角坐标系.
设抛物线解析式为y=ax2+3.
将点(-2,1)代入解析式,
可得1=a · (-2)2+3.
y
O
(2,1)
(-2,1)
水面
x
(0,3)
水面下降一米,即此时y=0.
虽然建立的直角坐标系不一样,但是两种方法的结果是相同的.
你还有其他的方法吗?
y
O
(2,0)
(-2,0)
x
(0,2)
还可以以水面未下降时的水面为x轴,以抛物线的对称轴为y轴建立直角坐标系来计算.
随堂演练
基础巩固
1.某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)( )
A.9.2 m B.9.1 m
C.9 m D.5.1 m
B
2.某涵洞是抛物线形,它的截面如图所示,现测得水平宽度AB=1.6m,涵洞顶点O到水面的距离为2.4m,那么在如图所示的直角坐标系中,涵洞所在的抛物线的解析式是 .
y=-3.75x2
A B
综合应用
3.某幢建筑物,从10米高的窗户A用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M离墙1米,
离地面 米,求水流落地点B离墙的距离.
拓展延伸
4.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为多少?
解:以水平面为x轴,抛物线对称轴为y轴建立直角坐标系.
设抛物线解析式为y=ax2+0.5,∵抛物线过点(1,0),
∴0=a+0.5,解得a=-0.5.
∴抛物线解析式为y=-0.5x2+0.5.
令y=0,则-0.5x2+0.5=0,解得x=±1.
令x=0.2,y=-0.5×0.22+0.5=0.48,
令x=0.6,y=-0.5×0.62+0.5=0.32.
(0.48+0.32)×2×100=160 (m)
∴这条防护栏需要不锈钢支柱
的总长度至少为160m.
课堂小结
利用二次函数解决抛物线形问题的一般步骤:
(1) 建立适当的直角坐标系;
(2) 写出抛物线上的关键点的坐标;
(3) 运用待定系数法求出函数关系式;
(4) 求解数学问题;
(5) 求解抛物线形实际问题.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
22.3 实际问题与二次函数
第3课时 抛物线形问题
R·九年级上册
新课导入
导入课题
问题:图中是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m. 水面下降1 m,水面宽度增加多少?
(1)能建立合适的直角坐标系,用二次函数的知识解决与抛物线相关的实际问题.
(2)进一步巩固二次函数的性质与图象特征.
学习目标
推进新课
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m. 水面下降1m时,水面宽度增加多少?
分析:
(1) 建立合适的直角坐标系;
(2) 将实际建筑数学化,数字化;
(3) 明确具体的数量关系,如函数解
析式;
(4) 分析所求问题,代入解析式求解。
探究
(2,-2)
(-2,-2)
x
y
O
解:
以拱顶为坐标原点建立如图所示的直角坐标系.
设抛物线解析式为y=ax2.
将点(-2,-2)代入解析式,
可得-2=a · (-2)2.
x
y
O
(2,-2)
(-2,-2)
水面
水面下降一米,即此时y=-3.
如果以下降1 m后的水面为x轴,以抛物线的对称轴为y轴,建立直角坐标系. 与前面方法的结果相同吗?
y
O
(2,1)
(-2,1)
水面
x
(0,3)
解:
依题意建立如图所示的直角坐标系.
设抛物线解析式为y=ax2+3.
将点(-2,1)代入解析式,
可得1=a · (-2)2+3.
y
O
(2,1)
(-2,1)
水面
x
(0,3)
水面下降一米,即此时y=0.
虽然建立的直角坐标系不一样,但是两种方法的结果是相同的.
你还有其他的方法吗?
y
O
(2,0)
(-2,0)
x
(0,2)
还可以以水面未下降时的水面为x轴,以抛物线的对称轴为y轴建立直角坐标系来计算.
随堂演练
基础巩固
1.某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)( )
A.9.2 m B.9.1 m
C.9 m D.5.1 m
B
2.某涵洞是抛物线形,它的截面如图所示,现测得水平宽度AB=1.6m,涵洞顶点O到水面的距离为2.4m,那么在如图所示的直角坐标系中,涵洞所在的抛物线的解析式是 .
y=-3.75x2
A B
综合应用
3.某幢建筑物,从10米高的窗户A用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M离墙1米,
离地面 米,求水流落地点B离墙的距离.
拓展延伸
4.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为多少?
解:以水平面为x轴,抛物线对称轴为y轴建立直角坐标系.
设抛物线解析式为y=ax2+0.5,∵抛物线过点(1,0),
∴0=a+0.5,解得a=-0.5.
∴抛物线解析式为y=-0.5x2+0.5.
令y=0,则-0.5x2+0.5=0,解得x=±1.
令x=0.2,y=-0.5×0.22+0.5=0.48,
令x=0.6,y=-0.5×0.62+0.5=0.32.
(0.48+0.32)×2×100=160 (m)
∴这条防护栏需要不锈钢支柱
的总长度至少为160m.
课堂小结
利用二次函数解决抛物线形问题的一般步骤:
(1) 建立适当的直角坐标系;
(2) 写出抛物线上的关键点的坐标;
(3) 运用待定系数法求出函数关系式;
(4) 求解数学问题;
(5) 求解抛物线形实际问题.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
