【高效备课】人教版九(上) 23.1 图形的旋转 第2课时 旋转作图与坐标系中的旋转变换 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 23.1 图形的旋转 第2课时 旋转作图与坐标系中的旋转变换 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:32 | ||
图片预览








文档简介
(共23张PPT)
23.1 图形的旋转
第2课时 旋转作图与坐标系中的旋转变换
R·九年级上册
新课导入
导入课题
如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是由某条线段绕O点旋转若干次所形成的图形?
A
B
C
D
E
F
O
学习目标
(1)能按要求作出简单平面图形旋转后的图形.
(2)能通过图形的旋转设计图案.
推进新课
知识点1
用旋转的知识画图
例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A D
B C
E
A D
B C
E
①因为A是旋转中心,所以A点的对应点是 .
②根据正方形的性质:AD=AB,∠ABD=90°,所
以点D的对应点是点 .
③因为旋转前、后的两个图形全等,所以本例根据三
角形全等的判定方法 ,作出△ADE的对应图
形为 .
A D
B C
E
E′
△ABE′
SAS
B
A
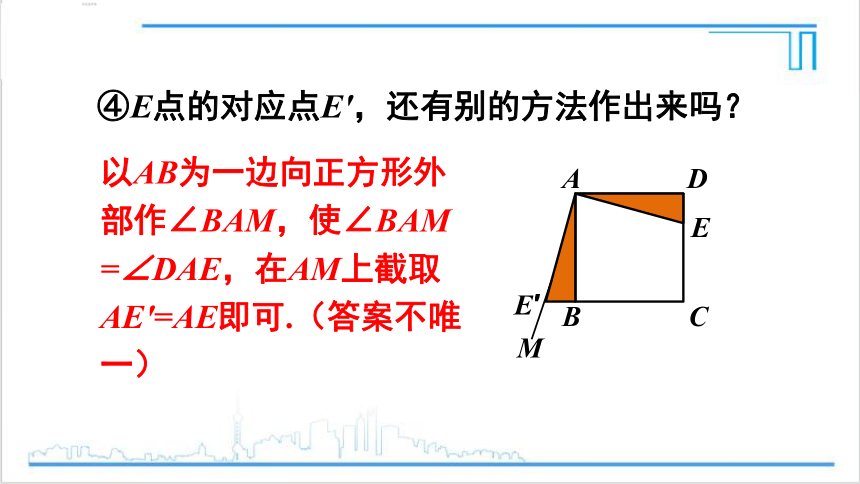
④E点的对应点E′,还有别的方法作出来吗?
以AB为一边向正方形外部作∠BAM,使∠BAM
=∠DAE,在AM上截取AE′=AE即可.(答案不唯一)
A D
B C
E
E′
M
观察课本上图案的变换过程,它们分别是改变旋转中的哪些要素旋转而成的?
O1
O2
O
α
O
β
a.旋转中心不变,旋转角改变,产生不同的旋转效果.
b.旋转角不变,旋转中心改变,产生不同的旋转效果.
任意画一个△ABC,以A为中心,把这个三角形逆时针旋转40°;
任意画一个△ABC,以AC中点为中心,把这个三角形旋转180°.
你能总结出旋转作图的一般步骤吗?
(1)分析图形,找出构成图形的关键点;
(2)确定三要素,即旋转中心、旋转角、旋转方向;
(3)将关键点分别与旋转中心连接后旋转,找到关
键点的对应点;
(4)顺次连接各对应点.
知识点2
用旋转的知识设计图形
运用旋转作图应满足三要素:旋转中心、旋转方向、旋转角,而旋转中心、旋转角固定下来,对应点就自然而然地固定下来.因此,选择不同的旋转中心、不同的旋转角会作出不同效果的图案.
你能利用旋转设计出美丽的图案吗?
B.
C. D.
随堂演练
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
C
2. 数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?
甲同学说:45°;乙同学说:60°;
丙同学说:90°;丁同学说:135°.
以上四位同学的回答中,错误的是
( )
A.甲 B.乙 C.丙 D.丁
B
3. 如图,在Rt△ABC中,∠ACB=90°,∠A=
40°,以直角顶点C为旋转中心,将△ABC旋
转到△A′B′C的位置,其中A′、B′分别是A、
B的对应点,且点B在斜边A′B′上,直角边C
A′交AB于点D,则旋转角等于( )
A.70° B.80° C.60° D.50°
B
4. 如图,△ABC中,∠C=90°,
∠B=40°,点D在边BC上,BD=
2CD.△ABC绕着点D顺时针旋转一定角度后,点B恰好落在初始△ABC的边上,求旋转角α(0°<α<180°)的度数.
解:有两种情况:
①点B落在AB上,如B′,∵DB=DB′, ∴∠BDB′=180-∠B-∠BB′D
=180°-40°-40°=100°,
即α=100°.
②点B落在AC上,如B″,在Rt△DCB″中,
∵B″D=BD=2CD,∴∠DB″C=30°,
∴∠B″DC=60°,∴∠BDB″=120°,
即α=120°.
综上所述:α的度数为100°或120°.
练习
【教材P62练习】
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
解:(1)如图,旋转中心不变,改变旋转角.
旋转角不变,改变旋转中心(答案不唯一)
练习
【教材P62练习】
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
解:(2)如图,旋转中心不变,改变旋转角.
旋转角不变,改变旋转中心(答案不唯一)
A
B
C
C′
B′
α
β
A
B
C
C′
B′
A
B
C
C′
B′
α
β
A
B
C
A′
B′
课堂小结
旋转作图
旋转中心
旋转方向
旋转角
顺时针
逆时针
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
23.1 图形的旋转
第2课时 旋转作图与坐标系中的旋转变换
R·九年级上册
新课导入
导入课题
如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是由某条线段绕O点旋转若干次所形成的图形?
A
B
C
D
E
F
O
学习目标
(1)能按要求作出简单平面图形旋转后的图形.
(2)能通过图形的旋转设计图案.
推进新课
知识点1
用旋转的知识画图
例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A D
B C
E
A D
B C
E
①因为A是旋转中心,所以A点的对应点是 .
②根据正方形的性质:AD=AB,∠ABD=90°,所
以点D的对应点是点 .
③因为旋转前、后的两个图形全等,所以本例根据三
角形全等的判定方法 ,作出△ADE的对应图
形为 .
A D
B C
E
E′
△ABE′
SAS
B
A
④E点的对应点E′,还有别的方法作出来吗?
以AB为一边向正方形外部作∠BAM,使∠BAM
=∠DAE,在AM上截取AE′=AE即可.(答案不唯一)
A D
B C
E
E′
M
观察课本上图案的变换过程,它们分别是改变旋转中的哪些要素旋转而成的?
O1
O2
O
α
O
β
a.旋转中心不变,旋转角改变,产生不同的旋转效果.
b.旋转角不变,旋转中心改变,产生不同的旋转效果.
任意画一个△ABC,以A为中心,把这个三角形逆时针旋转40°;
任意画一个△ABC,以AC中点为中心,把这个三角形旋转180°.
你能总结出旋转作图的一般步骤吗?
(1)分析图形,找出构成图形的关键点;
(2)确定三要素,即旋转中心、旋转角、旋转方向;
(3)将关键点分别与旋转中心连接后旋转,找到关
键点的对应点;
(4)顺次连接各对应点.
知识点2
用旋转的知识设计图形
运用旋转作图应满足三要素:旋转中心、旋转方向、旋转角,而旋转中心、旋转角固定下来,对应点就自然而然地固定下来.因此,选择不同的旋转中心、不同的旋转角会作出不同效果的图案.
你能利用旋转设计出美丽的图案吗?
B.
C. D.
随堂演练
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
C
2. 数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?
甲同学说:45°;乙同学说:60°;
丙同学说:90°;丁同学说:135°.
以上四位同学的回答中,错误的是
( )
A.甲 B.乙 C.丙 D.丁
B
3. 如图,在Rt△ABC中,∠ACB=90°,∠A=
40°,以直角顶点C为旋转中心,将△ABC旋
转到△A′B′C的位置,其中A′、B′分别是A、
B的对应点,且点B在斜边A′B′上,直角边C
A′交AB于点D,则旋转角等于( )
A.70° B.80° C.60° D.50°
B
4. 如图,△ABC中,∠C=90°,
∠B=40°,点D在边BC上,BD=
2CD.△ABC绕着点D顺时针旋转一定角度后,点B恰好落在初始△ABC的边上,求旋转角α(0°<α<180°)的度数.
解:有两种情况:
①点B落在AB上,如B′,∵DB=DB′, ∴∠BDB′=180-∠B-∠BB′D
=180°-40°-40°=100°,
即α=100°.
②点B落在AC上,如B″,在Rt△DCB″中,
∵B″D=BD=2CD,∴∠DB″C=30°,
∴∠B″DC=60°,∴∠BDB″=120°,
即α=120°.
综上所述:α的度数为100°或120°.
练习
【教材P62练习】
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
解:(1)如图,旋转中心不变,改变旋转角.
旋转角不变,改变旋转中心(答案不唯一)
练习
【教材P62练习】
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
解:(2)如图,旋转中心不变,改变旋转角.
旋转角不变,改变旋转中心(答案不唯一)
A
B
C
C′
B′
α
β
A
B
C
C′
B′
A
B
C
C′
B′
α
β
A
B
C
A′
B′
课堂小结
旋转作图
旋转中心
旋转方向
旋转角
顺时针
逆时针
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
