【高效备课】人教版九(上) 23.2 中心对称 23.2.3 关于原点对称的点的坐标 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 23.2 中心对称 23.2.3 关于原点对称的点的坐标 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 239.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:32 | ||
图片预览







文档简介
(共20张PPT)
23.2.3 关于原点对称的点的坐标
R·九年级上册
新课导入
导入课题
前面我们学习平移、对称变换时,把图形放到平面直角坐标系中,得到了平移、对称变换的点的坐标特征,这节课我们来探究关于原点对称的点的坐标特征.
学习目标
(1)能说出关于原点对称的点的坐标的关系.
(2)能在平面直角坐标系中画出已知图形关于原点对称的图形.
推进新课
知识点1
关于原点对称的点的坐标
在右图的直角坐标系中,作出下列已知点关于原点O的对称点.
A(4,0),B(0,-3),C(2,1),D(-1,2),E(-3,-4).
填 表:
已知点的坐标 A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-4)
关于原点对称的点的坐标
A′(-4,0)
B′(0,3)
C′(-2,-1)
D′(1,-2)
E′(3,4)
思考:通过填表,你有什么发现?
根据上表,一般地,两个点关于原点对称时,它们的坐标符号相反,即点P(x,y) 关于原点的对称点为P′(-x,-y).
强化训练:
①下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),
E(0,5),F(-2,1),G(-2,-1).
解:C、F关于原点O对称.
②已知点A(m-1,2),B(-3,n+1)两点关于原点对称,则m=____,n=_____.
4
-3
【教材P69练习 第1题】
知识点2
利用关于原点对称的点的坐标特征作图
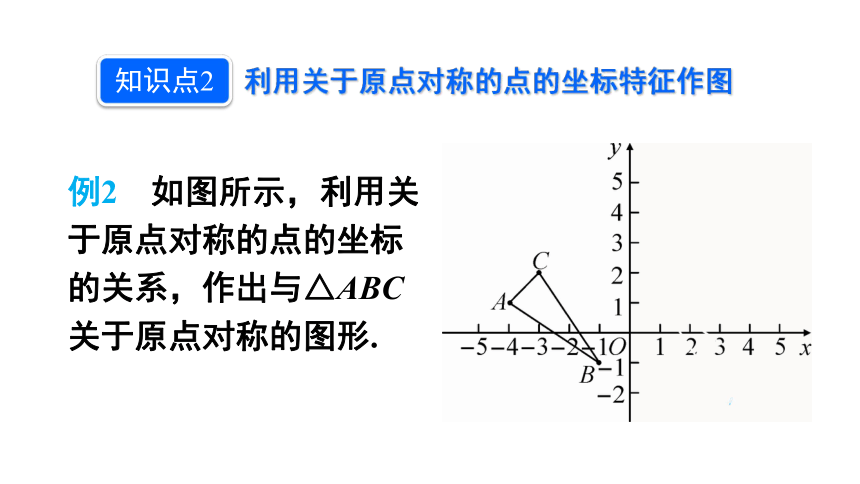
例2 如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC关于原点对称的图形.
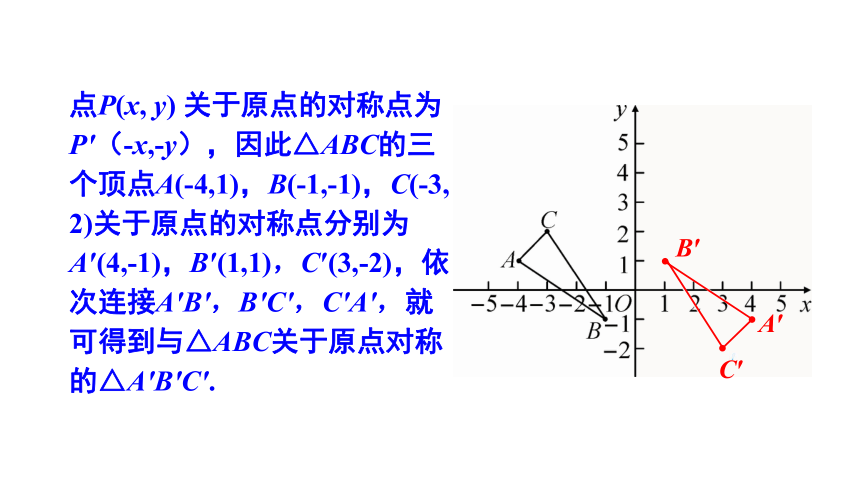
点P(x, y) 关于原点的对称点为P′(-x,-y),因此△ABC的三个顶点A(-4,1),B(-1,-1),C(-3,
2)关于原点的对称点分别为A′(4,-1),B′(1,1),C′(3,-2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于原点对称的△A′B′C′.
A′
B′
C′
利用关于原点对称的点的坐标的特征,作给定图形关于原点对称的图形的一般步骤是什么?
a.先找出给定图形上有代表性的点;
b.作这些点关于原点的对称点;
c.将这些点依次连接起来,就得到给定图形关于原点对称的图形.
已知如图,△ABC与△DEF关于原点O成中心对称,A(-1,2),C(-1,1),E(4,-3),则B、D、F的坐标分别为B(_____),D(_____),F(_____).
-4,3
1,-2
1,-1
随堂演练
1.点P(-3,1)关于原点的对称点P′的坐标是______ .
2.若P(5-2a,6)与Q(3,5b)关于原点对称,则a=___,
b=____.
3.将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘以-1,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.无法确定
(3,-1)
4
C
4.已知矩形ABCD的对称中心恰为原点O,且点A的坐标为(2, -3),则点C的坐标为( )
A.(-2,3) B.(-2,-3)
C.(2,3) D.(-3,2)
5.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
D
6.在如图所示的方格纸中,每个小正方形的边长均为1,如果以MN所在的直线为y轴,以小正方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则此时C点的坐标为( )
A.(1,3) B.(2,-1)
C.(2,1) D.(3,1)
B
7.如图,△DEF是由△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a、b的值.
解:(1)A(2,3),D(-2,-3),B(1,2),E(-1,-2),C(3,1),
F(-3,-1),对应点的坐标关于原点对称.
(2)∵点P(a+3,4-b)与点Q(2a,2b-3)关于原点对称.
∴a+3=-2a,4-b=3-2b.
∴a=-1,b=-1.
练习
【教材P69练习 第2题】
1. 写出下列各点关于原点O对称的点A′,B ′,C ′,D ′的坐标:
A(3,1),B(-2,3),C(-1,-2),D(2,-3).
解:A′(3,1),B′(-2,3),C′(-1,-2),D′(2,-3).
【教材P69练习 第3题】
2. 如图,已知点A的坐标为(-2 ,2),点B的坐标为(-1,- ),
菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标
解:C(2 ,-2),D(1, ).
A
B
O
D
C
y
x
课堂小结
点P(x,y) 关于原点的对称点为P′(-x,-y)
关于原点对称
横、纵坐标互为相反数
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
23.2.3 关于原点对称的点的坐标
R·九年级上册
新课导入
导入课题
前面我们学习平移、对称变换时,把图形放到平面直角坐标系中,得到了平移、对称变换的点的坐标特征,这节课我们来探究关于原点对称的点的坐标特征.
学习目标
(1)能说出关于原点对称的点的坐标的关系.
(2)能在平面直角坐标系中画出已知图形关于原点对称的图形.
推进新课
知识点1
关于原点对称的点的坐标
在右图的直角坐标系中,作出下列已知点关于原点O的对称点.
A(4,0),B(0,-3),C(2,1),D(-1,2),E(-3,-4).
填 表:
已知点的坐标 A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-4)
关于原点对称的点的坐标
A′(-4,0)
B′(0,3)
C′(-2,-1)
D′(1,-2)
E′(3,4)
思考:通过填表,你有什么发现?
根据上表,一般地,两个点关于原点对称时,它们的坐标符号相反,即点P(x,y) 关于原点的对称点为P′(-x,-y).
强化训练:
①下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),
E(0,5),F(-2,1),G(-2,-1).
解:C、F关于原点O对称.
②已知点A(m-1,2),B(-3,n+1)两点关于原点对称,则m=____,n=_____.
4
-3
【教材P69练习 第1题】
知识点2
利用关于原点对称的点的坐标特征作图
例2 如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC关于原点对称的图形.
点P(x, y) 关于原点的对称点为P′(-x,-y),因此△ABC的三个顶点A(-4,1),B(-1,-1),C(-3,
2)关于原点的对称点分别为A′(4,-1),B′(1,1),C′(3,-2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于原点对称的△A′B′C′.
A′
B′
C′
利用关于原点对称的点的坐标的特征,作给定图形关于原点对称的图形的一般步骤是什么?
a.先找出给定图形上有代表性的点;
b.作这些点关于原点的对称点;
c.将这些点依次连接起来,就得到给定图形关于原点对称的图形.
已知如图,△ABC与△DEF关于原点O成中心对称,A(-1,2),C(-1,1),E(4,-3),则B、D、F的坐标分别为B(_____),D(_____),F(_____).
-4,3
1,-2
1,-1
随堂演练
1.点P(-3,1)关于原点的对称点P′的坐标是______ .
2.若P(5-2a,6)与Q(3,5b)关于原点对称,则a=___,
b=____.
3.将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘以-1,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.无法确定
(3,-1)
4
C
4.已知矩形ABCD的对称中心恰为原点O,且点A的坐标为(2, -3),则点C的坐标为( )
A.(-2,3) B.(-2,-3)
C.(2,3) D.(-3,2)
5.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
D
6.在如图所示的方格纸中,每个小正方形的边长均为1,如果以MN所在的直线为y轴,以小正方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则此时C点的坐标为( )
A.(1,3) B.(2,-1)
C.(2,1) D.(3,1)
B
7.如图,△DEF是由△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a、b的值.
解:(1)A(2,3),D(-2,-3),B(1,2),E(-1,-2),C(3,1),
F(-3,-1),对应点的坐标关于原点对称.
(2)∵点P(a+3,4-b)与点Q(2a,2b-3)关于原点对称.
∴a+3=-2a,4-b=3-2b.
∴a=-1,b=-1.
练习
【教材P69练习 第2题】
1. 写出下列各点关于原点O对称的点A′,B ′,C ′,D ′的坐标:
A(3,1),B(-2,3),C(-1,-2),D(2,-3).
解:A′(3,1),B′(-2,3),C′(-1,-2),D′(2,-3).
【教材P69练习 第3题】
2. 如图,已知点A的坐标为(-2 ,2),点B的坐标为(-1,- ),
菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标
解:C(2 ,-2),D(1, ).
A
B
O
D
C
y
x
课堂小结
点P(x,y) 关于原点的对称点为P′(-x,-y)
关于原点对称
横、纵坐标互为相反数
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
