【高效备课】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.1 点和圆的位置关系 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.1 点和圆的位置关系 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 911.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:32 | ||
图片预览



文档简介
(共29张PPT)
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
R·九年级上册
新课导入
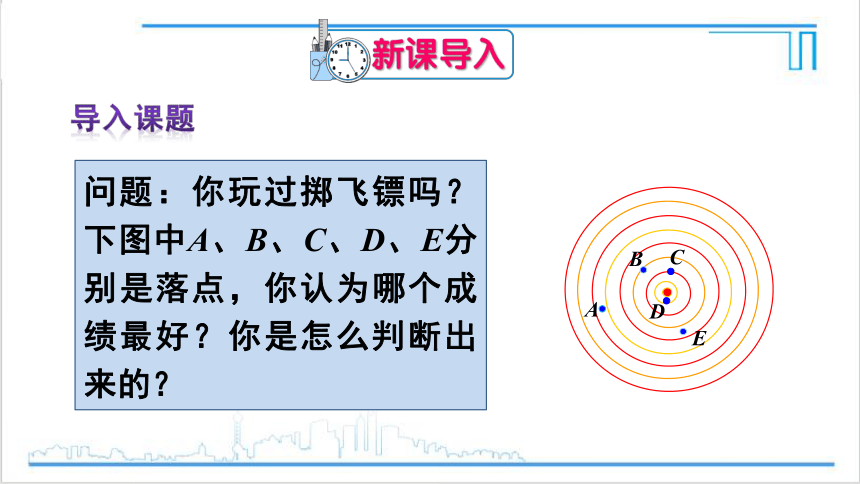
问题:你玩过掷飞镖吗?下图中A、B、C、D、E分别是落点,你认为哪个成绩最好?你是怎么判断出来的?
A
B
C
D
E
(1)知道点和圆的三种位置关系及其判定方法.
(2)知道不在同一直线上的三点确定一个圆,
能过不在同一直线上的三点作圆.
(3)知道三角形外心的概念及其性质.
(4)了解反证法的证明思想及一般步骤.
推进新课
r
·
C
O
A
B
OC > r
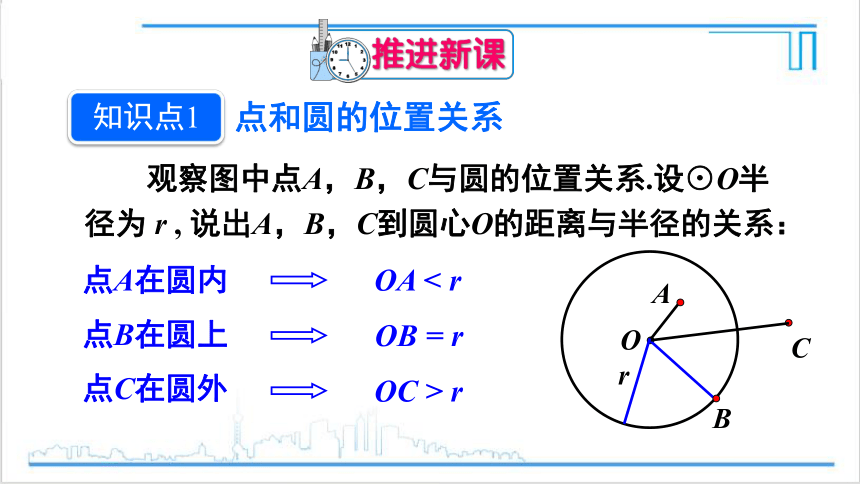
观察图中点A,B,C与圆的位置关系.设⊙O半径为 r , 说出A,B,C到圆心O的距离与半径的关系:
点C在圆外
点A在圆内
点B在圆上
OA < r
OB = r
知识点1
点和圆的位置关系
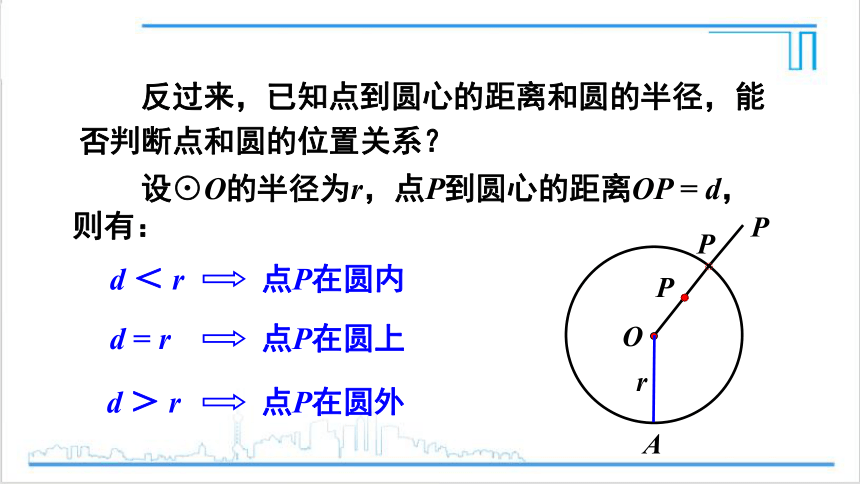
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
d = r
d > r
d < r
点P在圆内
点P在圆上
点P在圆外
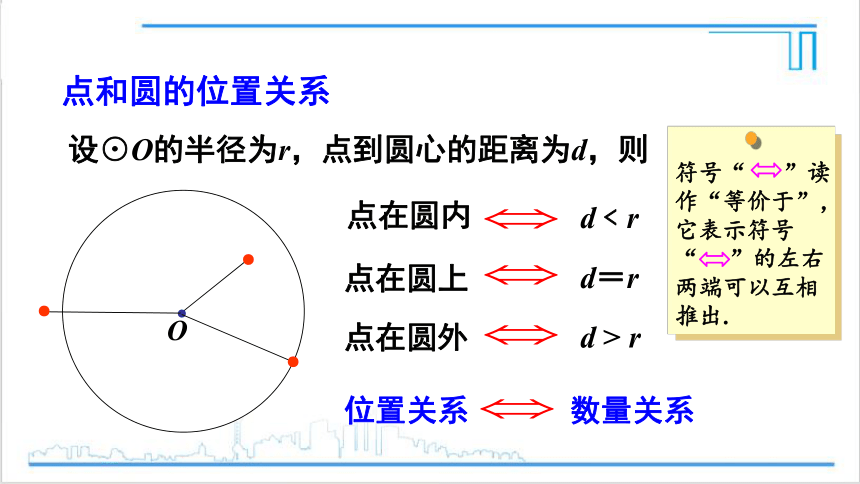
设⊙O的半径为r,点到圆心的距离为d,则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
●
●
●
●
O
位置关系 数量关系
符号“ ”读作“等价于”,它表示符号“ ”的左右两端可以互相推出.
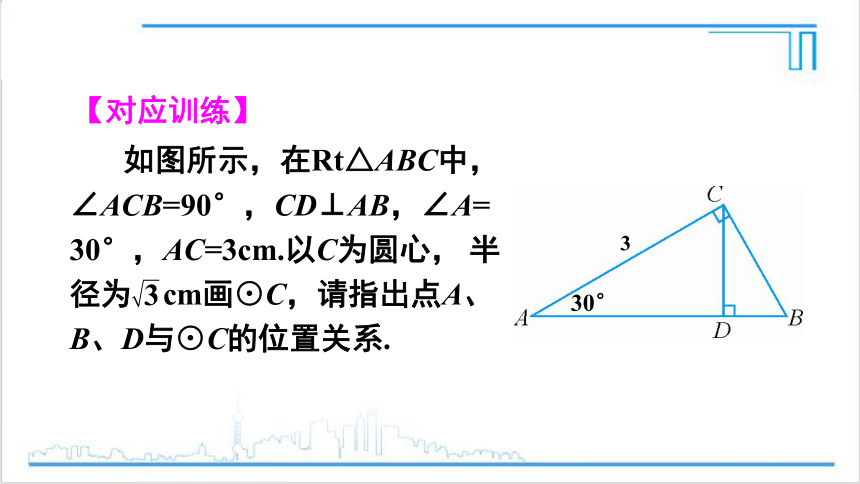
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A= 30°,AC=3cm.以C为圆心, 半径为 cm画⊙C,请指出点A、B、D与⊙C的位置关系.
【对应训练】
3
30°
解:在Rt△ACD中,∠A=30°,
∴点B在⊙C上;
由勾股定理得,AB=2 cm,BC= cm.
∵CD< cm,∴点D在⊙C内;
3
30°
∴CD= AC= ×3=1.5(cm).
AC=3cm> cm,∴点A在⊙C外.
知识点2
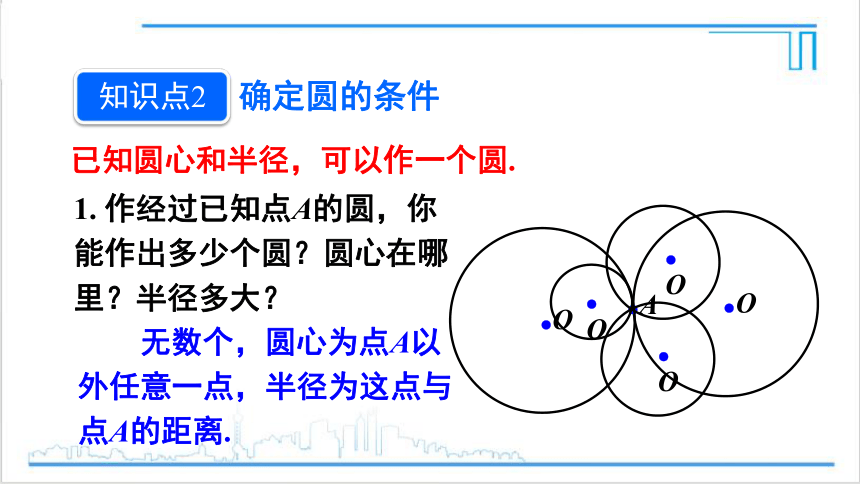
确定圆的条件
1. 作经过已知点A的圆,你能作出多少个圆?圆心在哪里?半径多大?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
已知圆心和半径,可以作一个圆.
2. 作经过已知点A、B的圆,你能作出多少个?圆心在哪里?
●
O
O
●
●
O
●
O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
3. 经过同一平面内三个点作圆,情况会怎样呢?
经过不在同一直线上的三点A、B、C能作出几个圆?圆心在哪里?
不在同一直线上的三个点确定一个圆.
┓
┏
●
B
●C
●A
●O
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做这个三角形的外心.
●
B
●A
●O
●C
想一想:
一个三角形有 个外接圆,
而一个圆有 个内接三角形.
一
无数
过同一直线上的三点可以作圆吗?
思考
●
●
●
怎么证明?
不能
证明:过同一直线上的三点不能作圆.
知识点3
反证法
如图,已知点A、B、C在直线m上.
求证:过点A、B、C不能作圆.
m
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到A、B、C三点的距离都相等,
即圆心是线段AB、BC垂直平分线的交点.
分别作AB、BC垂直平分线l1、l2.
显然l1∥l2,
l1与l2无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
A
B
C
l1
l2
反证法的步骤:
(1)假设原命题不成立;
(2)以此为依据进行推理,产生矛盾(与公理、定理或条件矛盾);
(3)得出假设不成立,从而原命题成立.
用反证法证明:等腰三角形的底角一定是锐角.
分析:由题目分析,“一定是锐角”的反面就是“不是锐角”,即是直角或钝角,因此应分两种情况讨论.
【对应训练】
已知:在△ABC中,AB=AC,求证:∠B,∠C一定是锐角.
证明:假设∠B,∠C不是锐角,则∠B,∠C是直角
或钝角.
(1)若∠B,∠C是直角,即∠B=∠C=90°,
故∠A+∠B+∠C >180°,
这与三角形的内角和定理矛盾,
所以∠B,∠C不是直角.
A
B
C
(2)若∠B,∠C是钝角,即∠B=∠C >90°,
故∠A+∠B+∠C >180°,
这与三角形的内角和定理矛盾,
所以∠B,∠C不是钝角.
综上所述,∠B,∠C不是直角也不是钝角,
即∠B,∠C是锐角,
所以等腰三角形的底角一定是锐角.
A
B
C
随堂演练
基础巩固
1.判断下列说法是否正确:
(1) 任意的一个三角形一定有一个外接圆.( )
(2) 任意一个圆有且只有一个内接三角形.( )
(3) 经过三点一定可以确定一个圆.( )
(4) 三角形的外心到三角形各顶点的距离相等.( )
√
√
×
×
2.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
3.若一个三角形的外心在一边上,则此三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
圆内
圆上
圆外
B
4.如图,分别作出锐角三角形、直角三角形、钝角三角形的外接圆,它们的外心位置有什么特点?
三角形内部
三角形斜边
中点处
三角形外部
5.爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,点导火索的人以每秒6.5m的速度撤离是否安全?为什么?
解:由题意可知,导火索燃烧完需18÷0.9=20(S).
又点导火索的人以每秒6.5m的速度撤离,
则导火索燃烧完时撤离的最大距离为6.5×20=130(m).
∵130>120,∴安全.
综合应用
6.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘要确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.
解:(1)在圆形瓷盘的边缘选A、B、C三点;
(2)连接AB、BC;
(3)分别作出AB、BC的垂直平分线;
(4)两垂直平分线的交点就是瓷盘的圆心.
拓展延伸
A
B
C
1. 画出由所有到已知点O的距离大于或等于2 cm,并且小于
或等于3 cm的点组成的图形.
练习
【教材P95练习 第1题】
3cm
2cm
如图所示,圆环即为所求图形。
2. 体育课上,小明和小丽的铅球成绩分别是6.4 m和5.1 m,
他们投出的铅球分别落在图中哪个区域内?
解:成绩为6.4m落在④的区域内,成绩为5.1m落在③的区域内.
【教材P95练习 第2题】
3. 如图,CD所在的直线垂直平分线段AB,怎样用这样的
工具找到圆形工件的圆心?
解:转动两次即可,CD所在的两条直线的交点就是圆心.
【教材P95练习 第2题】
A
B
C
D
课堂小结
点和圆的位置关系
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
确定圆的条件:
不在同一直线上的三个点确定一个圆.
反证法:
①反设,②推导出矛盾,③下结论
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
R·九年级上册
新课导入
问题:你玩过掷飞镖吗?下图中A、B、C、D、E分别是落点,你认为哪个成绩最好?你是怎么判断出来的?
A
B
C
D
E
(1)知道点和圆的三种位置关系及其判定方法.
(2)知道不在同一直线上的三点确定一个圆,
能过不在同一直线上的三点作圆.
(3)知道三角形外心的概念及其性质.
(4)了解反证法的证明思想及一般步骤.
推进新课
r
·
C
O
A
B
OC > r
观察图中点A,B,C与圆的位置关系.设⊙O半径为 r , 说出A,B,C到圆心O的距离与半径的关系:
点C在圆外
点A在圆内
点B在圆上
OA < r
OB = r
知识点1
点和圆的位置关系
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
d = r
d > r
d < r
点P在圆内
点P在圆上
点P在圆外
设⊙O的半径为r,点到圆心的距离为d,则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
●
●
●
●
O
位置关系 数量关系
符号“ ”读作“等价于”,它表示符号“ ”的左右两端可以互相推出.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A= 30°,AC=3cm.以C为圆心, 半径为 cm画⊙C,请指出点A、B、D与⊙C的位置关系.
【对应训练】
3
30°
解:在Rt△ACD中,∠A=30°,
∴点B在⊙C上;
由勾股定理得,AB=2 cm,BC= cm.
∵CD< cm,∴点D在⊙C内;
3
30°
∴CD= AC= ×3=1.5(cm).
AC=3cm> cm,∴点A在⊙C外.
知识点2
确定圆的条件
1. 作经过已知点A的圆,你能作出多少个圆?圆心在哪里?半径多大?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
已知圆心和半径,可以作一个圆.
2. 作经过已知点A、B的圆,你能作出多少个?圆心在哪里?
●
O
O
●
●
O
●
O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
3. 经过同一平面内三个点作圆,情况会怎样呢?
经过不在同一直线上的三点A、B、C能作出几个圆?圆心在哪里?
不在同一直线上的三个点确定一个圆.
┓
┏
●
B
●C
●A
●O
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做这个三角形的外心.
●
B
●A
●O
●C
想一想:
一个三角形有 个外接圆,
而一个圆有 个内接三角形.
一
无数
过同一直线上的三点可以作圆吗?
思考
●
●
●
怎么证明?
不能
证明:过同一直线上的三点不能作圆.
知识点3
反证法
如图,已知点A、B、C在直线m上.
求证:过点A、B、C不能作圆.
m
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到A、B、C三点的距离都相等,
即圆心是线段AB、BC垂直平分线的交点.
分别作AB、BC垂直平分线l1、l2.
显然l1∥l2,
l1与l2无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
A
B
C
l1
l2
反证法的步骤:
(1)假设原命题不成立;
(2)以此为依据进行推理,产生矛盾(与公理、定理或条件矛盾);
(3)得出假设不成立,从而原命题成立.
用反证法证明:等腰三角形的底角一定是锐角.
分析:由题目分析,“一定是锐角”的反面就是“不是锐角”,即是直角或钝角,因此应分两种情况讨论.
【对应训练】
已知:在△ABC中,AB=AC,求证:∠B,∠C一定是锐角.
证明:假设∠B,∠C不是锐角,则∠B,∠C是直角
或钝角.
(1)若∠B,∠C是直角,即∠B=∠C=90°,
故∠A+∠B+∠C >180°,
这与三角形的内角和定理矛盾,
所以∠B,∠C不是直角.
A
B
C
(2)若∠B,∠C是钝角,即∠B=∠C >90°,
故∠A+∠B+∠C >180°,
这与三角形的内角和定理矛盾,
所以∠B,∠C不是钝角.
综上所述,∠B,∠C不是直角也不是钝角,
即∠B,∠C是锐角,
所以等腰三角形的底角一定是锐角.
A
B
C
随堂演练
基础巩固
1.判断下列说法是否正确:
(1) 任意的一个三角形一定有一个外接圆.( )
(2) 任意一个圆有且只有一个内接三角形.( )
(3) 经过三点一定可以确定一个圆.( )
(4) 三角形的外心到三角形各顶点的距离相等.( )
√
√
×
×
2.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
3.若一个三角形的外心在一边上,则此三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
圆内
圆上
圆外
B
4.如图,分别作出锐角三角形、直角三角形、钝角三角形的外接圆,它们的外心位置有什么特点?
三角形内部
三角形斜边
中点处
三角形外部
5.爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,点导火索的人以每秒6.5m的速度撤离是否安全?为什么?
解:由题意可知,导火索燃烧完需18÷0.9=20(S).
又点导火索的人以每秒6.5m的速度撤离,
则导火索燃烧完时撤离的最大距离为6.5×20=130(m).
∵130>120,∴安全.
综合应用
6.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘要确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.
解:(1)在圆形瓷盘的边缘选A、B、C三点;
(2)连接AB、BC;
(3)分别作出AB、BC的垂直平分线;
(4)两垂直平分线的交点就是瓷盘的圆心.
拓展延伸
A
B
C
1. 画出由所有到已知点O的距离大于或等于2 cm,并且小于
或等于3 cm的点组成的图形.
练习
【教材P95练习 第1题】
3cm
2cm
如图所示,圆环即为所求图形。
2. 体育课上,小明和小丽的铅球成绩分别是6.4 m和5.1 m,
他们投出的铅球分别落在图中哪个区域内?
解:成绩为6.4m落在④的区域内,成绩为5.1m落在③的区域内.
【教材P95练习 第2题】
3. 如图,CD所在的直线垂直平分线段AB,怎样用这样的
工具找到圆形工件的圆心?
解:转动两次即可,CD所在的两条直线的交点就是圆心.
【教材P95练习 第2题】
A
B
C
D
课堂小结
点和圆的位置关系
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
确定圆的条件:
不在同一直线上的三个点确定一个圆.
反证法:
①反设,②推导出矛盾,③下结论
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
