【高效备课】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.2 直线和圆的位置关系 第1课时 直线和圆的位置关系 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.2 直线和圆的位置关系 第1课时 直线和圆的位置关系 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
R·九年级上册
新课导入
情景:如图,在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
问题:直线和圆有几种位置关系?怎样判断直线和圆的位置关系?
(1)知道直线和圆的位置关系及有关概念.
(2)会从公共点的个数或d和r的数量关系判定直线和圆的位置关系.
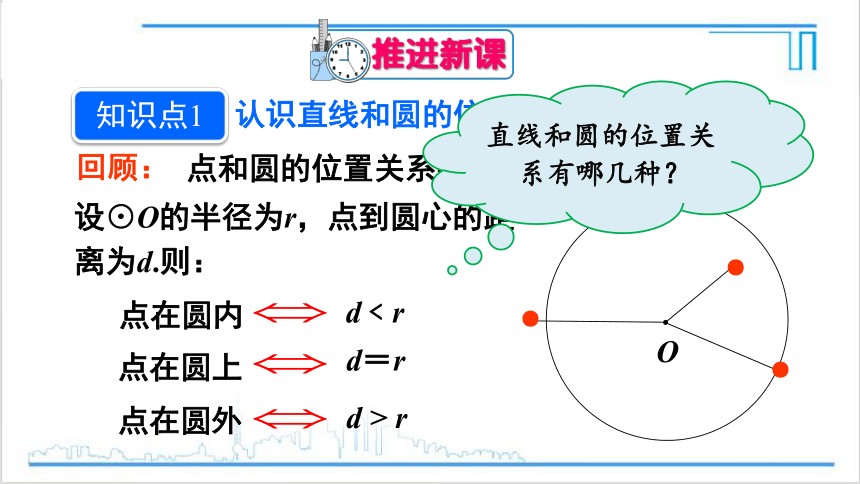
认识直线和圆的位置关系
点和圆的位置关系有哪几种?
回顾:
设⊙O的半径为r,点到圆心的距离为d.则:
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
●
●
●
.
O
推进新课
直线和圆的位置关系有哪几种?
知识点1
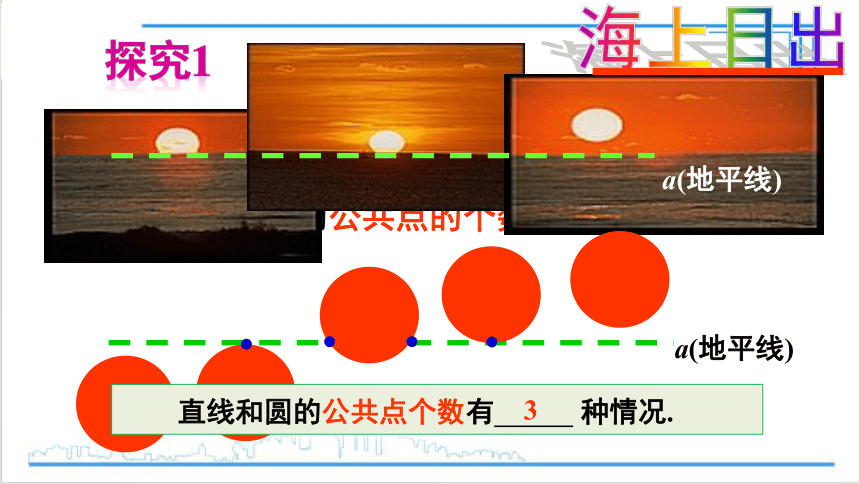
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
a(地平线)
a(地平线)
直线和圆的公共点个数有 种情况.
海上日出
●
●
●
●
探究1
3
●
●
●
●
按直线与圆的公共点的个数可分为:
个公共点
0
个公共点
1
个公共点
2
直线与圆的位置关系
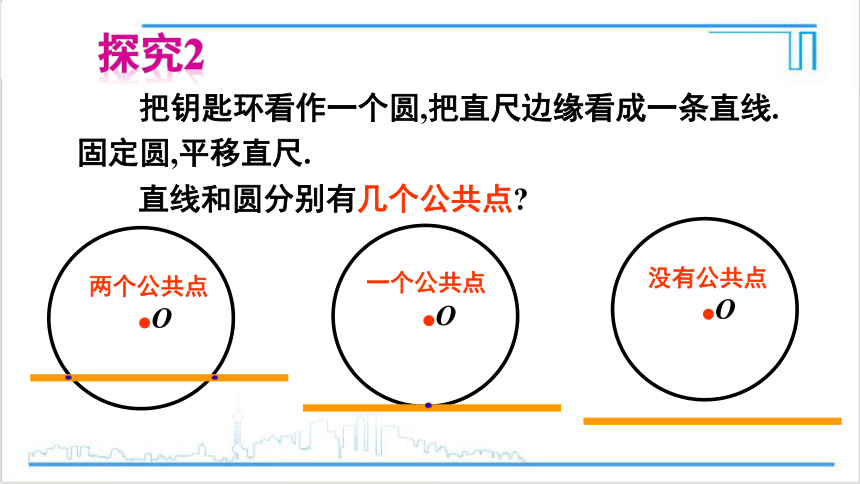
探究2
把钥匙环看作一个圆,把直尺边缘看成一条直线. 固定圆,平移直尺.
直线和圆分别有几个公共点
●O
●O
●O
两个公共点
没有公共点
一个公共点
0个公共点
.O
1个公共点
.O
2个公共点
.O
直线与圆相离
直线与圆相切
直线与圆相交
切线
.
切点
割线
现在你能总结出直线与圆的位置关系了吗?
.
.
交点
已知,直线与圆的位置关系有 种,分别是 、 、 .
判断直线和圆的位置关系
知识点2
3
相离
相切
相交
怎么判断直线和圆的位置关系呢?
快速判断下列各图中直线与圆的位置关系.
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1 .
直线l与 O2 .
O
●
●
●
●
●
相离
相交
从直线与圆公共点的个数可以判断出直线与圆的位置关系.
方法一:
还可以怎么判断直线和圆的位置关系?
过直线外一点作这条直线的垂线段, 垂线段的长度叫点到直线的距离.
l
.O
D
如图,设⊙O的半径为r,圆心O到直线l的距离为d.则d与⊙O的半径r的大小有什么关系
.O
.O
r
d
r
d
相离
相切
d r
<
d r
=
你能根据d与r的大小关系确定直线与圆的位置关系吗
.O
r
d
相交
d r
>
设⊙O的半径为r,圆心到直线的距离为d.则
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
.
O
l1
l2
l3
d
d
d
r
方法二:
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)由 大小关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳
随堂演练
基础巩固
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
2.直线l与半径为r的⊙O相离,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
C
A
3.⊙O的半径为4cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系为 .
4.如图,在Rt△ABC中,∠C=90°,
∠A=60°,BC=4cm,以点C为圆心,
3cm长为半径作圆,则⊙C与AB的
位置关系是 .
相切
相交
5.如图,已知∠AOB=30°,M为OB边上一点,OM=5cm,以点M为圆心,r为半径的⊙M与直线OA有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
解:过M作MN⊥OA,垂足为N.
∵∠AOB=30°,∠MNO=90°,
∴MN= OM=2.5cm.
所以(1)⊙M与直线OA相离,因为r(2)⊙M与直线OA相交,因为r>MN.
(3)⊙M与直线OA相切,因为r=MN.
6.已知⊙O的半径为 ,直线l与点O的距离为d,若直线l与⊙O有公共点,则( )
A.d﹥ B.d= C.d﹤ D.d≤
7.直线l 和⊙O有公共点,则直线l与⊙O( )
A.相离 B.相切 C.相交 D.相切或相交
综合应用
D
D
8.如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为 .
解析:若与OA,AB,BC三条边相切,D的坐
标为(3,1);若与OA,BC,CO三条边相切,
D的坐标为(1,1);若与OA,AB,CO三条边
相切,D的坐标为(2,2);若与AB,BC,CO三
条边相切,D的坐标为(2,0).
拓展延伸
(1,1),(3,1)(2,2)和(2,0)
圆的直径是13cm,如果圆心与直线的距离分别是:
(1)4.5cm; (2)6.5cm; (3)8cm.
那么直线和圆分别是什么位置关系?有几个公共点?
练习
【教材P96练习】
解:(1)相交,有2个公共点;
(2)相切,有1个公共点;
(3)相离,没有公共点.
课堂小结
直线与圆的位置关系
相离
相切
相交
大致图象
数量关系(d、r)
交点个数
0
1
2
d﹤r
d=r
d > r
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
R·九年级上册
新课导入
情景:如图,在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
问题:直线和圆有几种位置关系?怎样判断直线和圆的位置关系?
(1)知道直线和圆的位置关系及有关概念.
(2)会从公共点的个数或d和r的数量关系判定直线和圆的位置关系.
认识直线和圆的位置关系
点和圆的位置关系有哪几种?
回顾:
设⊙O的半径为r,点到圆心的距离为d.则:
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
●
●
●
.
O
推进新课
直线和圆的位置关系有哪几种?
知识点1
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
a(地平线)
a(地平线)
直线和圆的公共点个数有 种情况.
海上日出
●
●
●
●
探究1
3
●
●
●
●
按直线与圆的公共点的个数可分为:
个公共点
0
个公共点
1
个公共点
2
直线与圆的位置关系
探究2
把钥匙环看作一个圆,把直尺边缘看成一条直线. 固定圆,平移直尺.
直线和圆分别有几个公共点
●O
●O
●O
两个公共点
没有公共点
一个公共点
0个公共点
.O
1个公共点
.O
2个公共点
.O
直线与圆相离
直线与圆相切
直线与圆相交
切线
.
切点
割线
现在你能总结出直线与圆的位置关系了吗?
.
.
交点
已知,直线与圆的位置关系有 种,分别是 、 、 .
判断直线和圆的位置关系
知识点2
3
相离
相切
相交
怎么判断直线和圆的位置关系呢?
快速判断下列各图中直线与圆的位置关系.
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1 .
直线l与 O2 .
O
●
●
●
●
●
相离
相交
从直线与圆公共点的个数可以判断出直线与圆的位置关系.
方法一:
还可以怎么判断直线和圆的位置关系?
过直线外一点作这条直线的垂线段, 垂线段的长度叫点到直线的距离.
l
.O
D
如图,设⊙O的半径为r,圆心O到直线l的距离为d.则d与⊙O的半径r的大小有什么关系
.O
.O
r
d
r
d
相离
相切
d r
<
d r
=
你能根据d与r的大小关系确定直线与圆的位置关系吗
.O
r
d
相交
d r
>
设⊙O的半径为r,圆心到直线的距离为d.则
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
.
O
l1
l2
l3
d
d
d
r
方法二:
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)由 大小关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳
随堂演练
基础巩固
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
2.直线l与半径为r的⊙O相离,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
C
A
3.⊙O的半径为4cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系为 .
4.如图,在Rt△ABC中,∠C=90°,
∠A=60°,BC=4cm,以点C为圆心,
3cm长为半径作圆,则⊙C与AB的
位置关系是 .
相切
相交
5.如图,已知∠AOB=30°,M为OB边上一点,OM=5cm,以点M为圆心,r为半径的⊙M与直线OA有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
解:过M作MN⊥OA,垂足为N.
∵∠AOB=30°,∠MNO=90°,
∴MN= OM=2.5cm.
所以(1)⊙M与直线OA相离,因为r
(3)⊙M与直线OA相切,因为r=MN.
6.已知⊙O的半径为 ,直线l与点O的距离为d,若直线l与⊙O有公共点,则( )
A.d﹥ B.d= C.d﹤ D.d≤
7.直线l 和⊙O有公共点,则直线l与⊙O( )
A.相离 B.相切 C.相交 D.相切或相交
综合应用
D
D
8.如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为 .
解析:若与OA,AB,BC三条边相切,D的坐
标为(3,1);若与OA,BC,CO三条边相切,
D的坐标为(1,1);若与OA,AB,CO三条边
相切,D的坐标为(2,2);若与AB,BC,CO三
条边相切,D的坐标为(2,0).
拓展延伸
(1,1),(3,1)(2,2)和(2,0)
圆的直径是13cm,如果圆心与直线的距离分别是:
(1)4.5cm; (2)6.5cm; (3)8cm.
那么直线和圆分别是什么位置关系?有几个公共点?
练习
【教材P96练习】
解:(1)相交,有2个公共点;
(2)相切,有1个公共点;
(3)相离,没有公共点.
课堂小结
直线与圆的位置关系
相离
相切
相交
大致图象
数量关系(d、r)
交点个数
0
1
2
d﹤r
d=r
d > r
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
