【高效备课】人教版九(上) 25.1 随机事件与概率 25.1.2 概率 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 25.1 随机事件与概率 25.1.2 概率 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:40 | ||
图片预览











文档简介
(共32张PPT)
25.1 随机事件与概率
25.1.2 概率
R·九年级上册
新课导入
导入课题
在同样条件下,某一随机事件可能发生也可能不发生.那么它发生的可能性有多大呢 能否用数值进行刻画呢
(1)理解概率的概念,知道概率的值与事件发生的可能性大小的对应关系.
(2)会运用列举法求一步实验和简单两步实验中事件发生的概率.
(3)会根据几何图形的面积求事件发生的概率.
学习目标
推进新课
知识点1
概率的意义与计算求值
从分别写有数字1,2,3,4,5的五个纸团中随机抽取一个,这个纸团里的数字有 种可能,即 .
在上节课问题1中:
5
1,2,3,4,5
抽到1的可能性与抽到2的可能性一样吗?它们的可能性是多少呢?
因为纸团看上去完全一样,又是随机抽取,所以每个数字被抽到的可能性大小相等.
那么抽到数字1,2,3,4,5这五种可能的概率都可以用 表示.
掷一枚骰子,向上一面的点数有6种可能,即
1,2,3,4,5,6.
因为骰子形状规则、质地均匀,又是随机掷出,所以每种点数出现的可能性大小 .我们可以用 表示每一种点数出现的可能性大小.
在上节课问题2中:
相等
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率.记作:P(A).
如问题1中:
由问题1和问题2,可以发现两个试验有什么共同特征?
①一次试验中,可能出现的结果只有有限个;
②一次试验中,各种结果出现的可能性相等.
抽纸团,抽到偶数的概率是多少?
在问题1中:
“抽到偶数”这个事件包含抽到2,4这两种可能结果,在全部5种可能的结果中所占的比为 .
你能求出“抽到奇数”这个事件的概率吗?
归纳
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性相等,事件A包括其中的m种结果,那么事件A发生的概率P(A)= .
在P(A)= 中,由m和n的含义,可知0≤m ≤n,进而有0≤ ≤1.
因此,
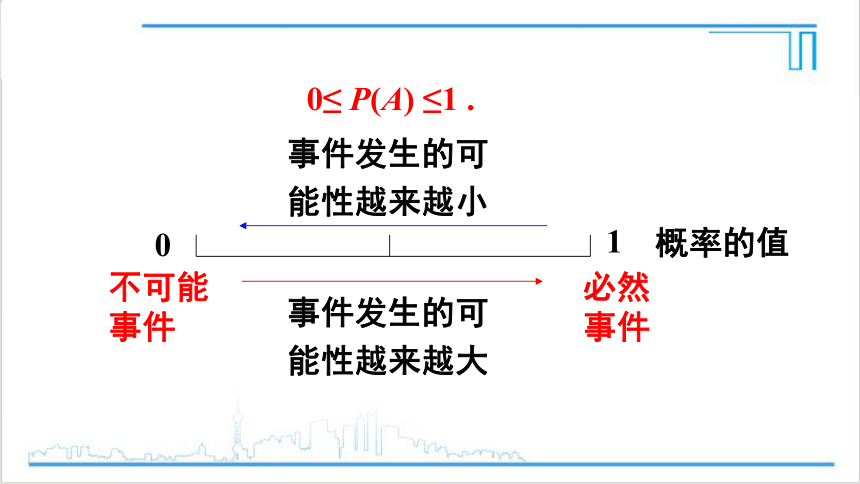
0≤ P(A) ≤1 .
不可能事件
必然事件
0
1
概率的值
0≤ P(A) ≤1 .
事件发生的可能性越来越小
事件发生的可能性越来越大
必然事件
不可能事件
事件A发生的概率表示为
P(A)=
事件A发生的结果数
所有可能的结果总数
例1 掷一枚质地均匀的骰子,观察向上一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5.
典例解析
(1)P(点数为2)=
(2)P(点数为奇数)=
(3)P(点数大于2且小于5)=
(1)、(2)、(3)掷到哪个的可能性大一点?
解:
例2 如图所示是一个可以自由转动的转盘,转盘分成7个大小相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形). 求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
结合(1)、(3)你发现了什么
知识点2
用面积法求概率
两个相反事件发生的概率和为1.
小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如下图),然后蒙上眼睛,并在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内(半径为3m的圆内)不算.你认为游戏公平吗?为什么?
P(小红胜)=
P(小明胜)=
做一做
区域事件发生的概率:
在与图形有关的概率问题中,概率的大小往往与面积有关.
一个平面区域内的每个点,事件发生的可能性都是相等的.如果所有可能发生的区域面积为S,所求事件A发生的区域面积为S′,
则P(A)= .
随堂演练
基础巩固
1.“明天降水的概率是15%”,下列说法中,正确的是( )
A.明天降水的可能性较小
B.明天将有15%的时间降水
C.明天将有15%的地区降水
D.明天肯定不降水
A
2.事件A:打开电视,它正在播广告;事件B:抛掷一枚质地均匀的骰子,朝上的点数小于7;事件C:在标准大气压下,温度低于0℃时冰融化.3个事件发生的概率分别记为P(A)、P(B)、P(C),则 P(A)、P(B)、P(C)的大小关系正确的是( )
A.P(C)<P(A)= P(B) B.P(C)<P(A)<P(B)
C.P(C)<P(B)<P(A) D.P(A)<P(B)<P(C)
B
3.如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )
B
4.抛掷一枚质地均匀的硬币,向上一面有几种可能的结果?它们的可能性相等吗?由此能得到“正面向上”的概率吗?
5.10件外观相同的产品中有1件不合格.现从中任意抽取1件进行检测,抽到不合格产品的概
率为 .
【教材P133练习 第1题】
有两种可能的结果,它们的可能性相等,“正面向上”的概率为 .
6.袋子中有2个红球,3个绿球和4个蓝球,它们只有颜色上的区别.从袋子中随机地取出一个球.
(1)能够事先确定取出的球是哪种颜色的吗?
(2)取出每种颜色的球的概率会相等吗?
(3)你认为取出哪种颜色的球的概率最大?
解:(1)不能;
(2)不相等;
(3)蓝球.
7.不透明的袋子里有1个红球,3个白球,5个黄球,每个球除颜色外都相同,从中任意摸1个球:
(1)摸到红球的概率是多少?
(2)摸到白球的概率是多少?
(3)摸到黄球的概率是多少?
8.如图是一个转盘.转盘分成8个相同的部分,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形).求下列事件的概率:
(1)指针指向红色;
(2)指针指向黄色或绿色.
解: (1)
综合应用
9.盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是 ,写出表示x和y关系的表达式;
x枚
y枚
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为 ,求x和y的值.
∴x+10=y,
又5x=3y,
∴x=15,y=25.
x+10枚
y枚
5x=3y
拓展延伸
10.如图是计算机中的一种益智小游戏“扫雷”的画面,在一个9×9的小方格的正方形雷区中,随机埋藏着10颗地雷,每个小方格内最多只能埋藏1颗地雷.
小红在游戏开始时首先随机地点击一个方格,该方格中出现了数字“3”,其意义表示该格的外围区域(图中阴影部分,记为A区域)有3颗地雷;接着,小红又点击了左上角第一个方格,出现了数字“1”,其外围区域(图中阴影部分)记为B区域;“A区域与B区域以及出现数字‘1’和‘3’两格”以外的部分记为C区域.
小红在下一步点击时要尽可能地避开地雷,那么她应点击A、B、C中的哪个区域?请说明理由.
即点击C区域遇到地雷的可能性最小,
所以小红在下一步点击时应点击C区域.
练习
【教材P133练习 第2题】
1. 不进明袋子中装有5个红球、3个绿球,这些球除了颜色外
无其他差别.从袋子中随机摸出1个球,“摸出红球”和“
摸出绿球”的可能性相等吗?它们的概率分别为多少?
可能性不相等,“摸出红球”的概率为 ,“摸出绿球”的概率为 .
【教材P133练习 第3题】
2. 回顾例3,如果小王在游戏开始时点击的第一个方格出现标
号1,那么下一步点去哪个区城比较安全
标号1表示在A区域有1颗地雷,在A区域遇到地雷的概率为 。B区域中共有9×9-9= 72(个)小方格,其中有10-1=9(颗)地雷,因此,点击B区域的任一方格遇到地雷的概率为 = .
由于 = ,故下一步点击哪一区域都是一样的.
课堂小结
1.概率的定义及基本性质
2.必然事件A: P(A)=1
不可能事件B: P(B)=0
随机事件C: 0<P(C)<1
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性相等,事件A包括其中的m种结果,那么事件A发生的概率P(A)= .
0≤ ≤1
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
25.1 随机事件与概率
25.1.2 概率
R·九年级上册
新课导入
导入课题
在同样条件下,某一随机事件可能发生也可能不发生.那么它发生的可能性有多大呢 能否用数值进行刻画呢
(1)理解概率的概念,知道概率的值与事件发生的可能性大小的对应关系.
(2)会运用列举法求一步实验和简单两步实验中事件发生的概率.
(3)会根据几何图形的面积求事件发生的概率.
学习目标
推进新课
知识点1
概率的意义与计算求值
从分别写有数字1,2,3,4,5的五个纸团中随机抽取一个,这个纸团里的数字有 种可能,即 .
在上节课问题1中:
5
1,2,3,4,5
抽到1的可能性与抽到2的可能性一样吗?它们的可能性是多少呢?
因为纸团看上去完全一样,又是随机抽取,所以每个数字被抽到的可能性大小相等.
那么抽到数字1,2,3,4,5这五种可能的概率都可以用 表示.
掷一枚骰子,向上一面的点数有6种可能,即
1,2,3,4,5,6.
因为骰子形状规则、质地均匀,又是随机掷出,所以每种点数出现的可能性大小 .我们可以用 表示每一种点数出现的可能性大小.
在上节课问题2中:
相等
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率.记作:P(A).
如问题1中:
由问题1和问题2,可以发现两个试验有什么共同特征?
①一次试验中,可能出现的结果只有有限个;
②一次试验中,各种结果出现的可能性相等.
抽纸团,抽到偶数的概率是多少?
在问题1中:
“抽到偶数”这个事件包含抽到2,4这两种可能结果,在全部5种可能的结果中所占的比为 .
你能求出“抽到奇数”这个事件的概率吗?
归纳
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性相等,事件A包括其中的m种结果,那么事件A发生的概率P(A)= .
在P(A)= 中,由m和n的含义,可知0≤m ≤n,进而有0≤ ≤1.
因此,
0≤ P(A) ≤1 .
不可能事件
必然事件
0
1
概率的值
0≤ P(A) ≤1 .
事件发生的可能性越来越小
事件发生的可能性越来越大
必然事件
不可能事件
事件A发生的概率表示为
P(A)=
事件A发生的结果数
所有可能的结果总数
例1 掷一枚质地均匀的骰子,观察向上一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5.
典例解析
(1)P(点数为2)=
(2)P(点数为奇数)=
(3)P(点数大于2且小于5)=
(1)、(2)、(3)掷到哪个的可能性大一点?
解:
例2 如图所示是一个可以自由转动的转盘,转盘分成7个大小相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形). 求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
结合(1)、(3)你发现了什么
知识点2
用面积法求概率
两个相反事件发生的概率和为1.
小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如下图),然后蒙上眼睛,并在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内(半径为3m的圆内)不算.你认为游戏公平吗?为什么?
P(小红胜)=
P(小明胜)=
做一做
区域事件发生的概率:
在与图形有关的概率问题中,概率的大小往往与面积有关.
一个平面区域内的每个点,事件发生的可能性都是相等的.如果所有可能发生的区域面积为S,所求事件A发生的区域面积为S′,
则P(A)= .
随堂演练
基础巩固
1.“明天降水的概率是15%”,下列说法中,正确的是( )
A.明天降水的可能性较小
B.明天将有15%的时间降水
C.明天将有15%的地区降水
D.明天肯定不降水
A
2.事件A:打开电视,它正在播广告;事件B:抛掷一枚质地均匀的骰子,朝上的点数小于7;事件C:在标准大气压下,温度低于0℃时冰融化.3个事件发生的概率分别记为P(A)、P(B)、P(C),则 P(A)、P(B)、P(C)的大小关系正确的是( )
A.P(C)<P(A)= P(B) B.P(C)<P(A)<P(B)
C.P(C)<P(B)<P(A) D.P(A)<P(B)<P(C)
B
3.如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )
B
4.抛掷一枚质地均匀的硬币,向上一面有几种可能的结果?它们的可能性相等吗?由此能得到“正面向上”的概率吗?
5.10件外观相同的产品中有1件不合格.现从中任意抽取1件进行检测,抽到不合格产品的概
率为 .
【教材P133练习 第1题】
有两种可能的结果,它们的可能性相等,“正面向上”的概率为 .
6.袋子中有2个红球,3个绿球和4个蓝球,它们只有颜色上的区别.从袋子中随机地取出一个球.
(1)能够事先确定取出的球是哪种颜色的吗?
(2)取出每种颜色的球的概率会相等吗?
(3)你认为取出哪种颜色的球的概率最大?
解:(1)不能;
(2)不相等;
(3)蓝球.
7.不透明的袋子里有1个红球,3个白球,5个黄球,每个球除颜色外都相同,从中任意摸1个球:
(1)摸到红球的概率是多少?
(2)摸到白球的概率是多少?
(3)摸到黄球的概率是多少?
8.如图是一个转盘.转盘分成8个相同的部分,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形).求下列事件的概率:
(1)指针指向红色;
(2)指针指向黄色或绿色.
解: (1)
综合应用
9.盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是 ,写出表示x和y关系的表达式;
x枚
y枚
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为 ,求x和y的值.
∴x+10=y,
又5x=3y,
∴x=15,y=25.
x+10枚
y枚
5x=3y
拓展延伸
10.如图是计算机中的一种益智小游戏“扫雷”的画面,在一个9×9的小方格的正方形雷区中,随机埋藏着10颗地雷,每个小方格内最多只能埋藏1颗地雷.
小红在游戏开始时首先随机地点击一个方格,该方格中出现了数字“3”,其意义表示该格的外围区域(图中阴影部分,记为A区域)有3颗地雷;接着,小红又点击了左上角第一个方格,出现了数字“1”,其外围区域(图中阴影部分)记为B区域;“A区域与B区域以及出现数字‘1’和‘3’两格”以外的部分记为C区域.
小红在下一步点击时要尽可能地避开地雷,那么她应点击A、B、C中的哪个区域?请说明理由.
即点击C区域遇到地雷的可能性最小,
所以小红在下一步点击时应点击C区域.
练习
【教材P133练习 第2题】
1. 不进明袋子中装有5个红球、3个绿球,这些球除了颜色外
无其他差别.从袋子中随机摸出1个球,“摸出红球”和“
摸出绿球”的可能性相等吗?它们的概率分别为多少?
可能性不相等,“摸出红球”的概率为 ,“摸出绿球”的概率为 .
【教材P133练习 第3题】
2. 回顾例3,如果小王在游戏开始时点击的第一个方格出现标
号1,那么下一步点去哪个区城比较安全
标号1表示在A区域有1颗地雷,在A区域遇到地雷的概率为 。B区域中共有9×9-9= 72(个)小方格,其中有10-1=9(颗)地雷,因此,点击B区域的任一方格遇到地雷的概率为 = .
由于 = ,故下一步点击哪一区域都是一样的.
课堂小结
1.概率的定义及基本性质
2.必然事件A: P(A)=1
不可能事件B: P(B)=0
随机事件C: 0<P(C)<1
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性相等,事件A包括其中的m种结果,那么事件A发生的概率P(A)= .
0≤ ≤1
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
