【高效备课】人教版九(上) 第21章 一元二次方程 数学活动 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 第21章 一元二次方程 数学活动 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
数学活动
R·九年级上册
新课导入
导入课题
点是几何中最基本的图形,许多点排列起来可以组成一个点阵.
今天我们就来看看点阵中隐藏了什么有趣的数学规律.
(1)通过观察点阵(数学模型),了解并掌握一些点阵及数学模型的变化规律.
(2)探究三角点阵中前n行的点数和的计算公式.
(3)运用一元二次方程的知识和三角点阵中前n行的点数和的计算公式解决问题.
(4)通过活动,培养学生的观察、比较、归纳和概括能力,培养学生的空间想象能力.
活动目标
推进新课
图1是一个三角形点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点…….
观察图形,完成下面各题.
·
··
···
····
·····
······
·······
……
图 1
活 动 1
三角形点阵
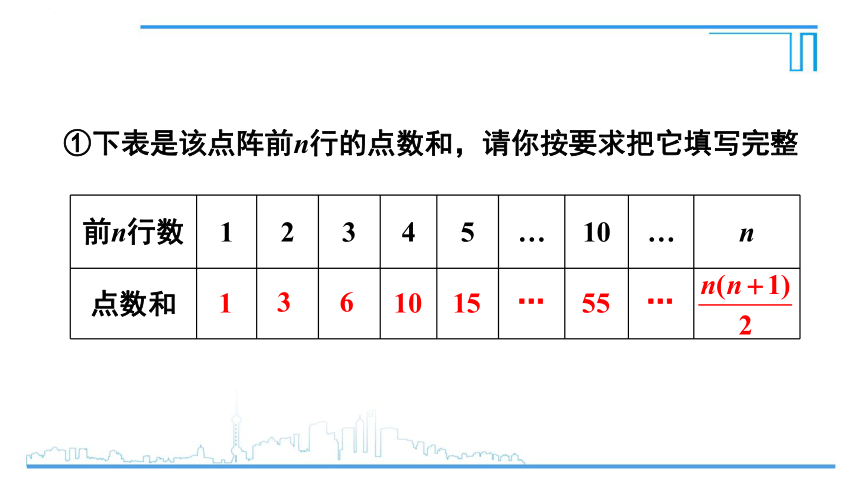
①下表是该点阵前n行的点数和,请你按要求把它填写完整
前n行数 1 2 3 4 5 … 10 … n
点数和
1
3
6
10
15
…
…
55
②若该三角点阵前n行的点数和是300,求行数n.
由①知.前n行的点数和为 ,解得n1=24,n2=-25(舍去),即行数n为24.
③该三角点阵前n行的点数和能是600吗?如果能,求出其行数n;如果不能,请说明理由.
前n行的点数和 ,解得n1= , n2= ,因为n是正整数,方程的两根均不符合条件,所以三角点阵前n行的点数和不能是600.
④如果把图中的三角点阵中各行的点数依次换为2,4,6,…,2n,…,你能探究出前n行的点数和满足什么规律吗?
前n行的点数和为
⑤在④中,三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明理由.
依题意,n(n+1)=600.
解得n1=24,n2=-25(舍去).
活 动 2
正六边形点阵
如图2 是一个形如正六边形的点阵,它的中心是一个点,算作第一层,第二层每边有两个点,第三层每边有三个点,……,依此类推.
图 2
·····
······
·······
········
·········
········
·······
······
·····
①填写下表:
层 数 1 2 3 4 …
该层对应的点数
所有层的总点数
1
6
12
18
…
1
7
19
37
…
②第n层所对应的点数为 (n≥2).
③写出n层正六边形点阵的总点数(n≥2);
6(n-1)
1+6×1+6×2+…+6(n-1)
=1+6·
=1+3n(n-1)
④如果点阵中所有层的总点数为331,请求出它共有几层?
1+3n(n-1)=331
化简方程为:n2-n-110=0
分解因式为:(n-11)(n+10)=0
解得:n1=11,n2=-10(舍去),
所以共有11层.
⑤ 点阵设计大赛:
设计时间:5分钟.
设计要求:
a .每人设计一组有规律、美观的点阵图,画出前4个点阵,并仿照三角形点阵的探究提出问题,然后在小组内交流自己的设计方案.
b.每组评选出优秀作品,派代表说明设计的方法及点阵中的规律.
随堂演练
1. 古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律.
(1)下图反映了一个“三角形数”是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
·
··
···
····
·
··
···
·
··
·
①1=1;
②1+2= ;
③1+2+3= ;
④1+2+3+4= .
3
6
10
(2)通过猜想,写出(1)中与第九个点阵相对应的等式: 。
(3)2015是“三角形数”吗?为什么?
1+2+3+…+9=45
解:不是.“三角形数”都可以写成 的形式,
令2015= ,
解得n1= ,n2= .
因为n是正整数,方程的两根均不符合条件,所以2015不是“三角形”数.
(4)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
··
··
·
···
···
···
····
····
····
····
·····
·····
·····
·····
·····
①1=12; ②1+3=22;
③3+6=32; ④6+10=42;
⑤ .
10+15=52
(5)通过猜想,写出(4)中与第n个点阵相对应的等式: .
(6)判断225是不是“正方形数”,如果不是,说明理由;如果是,225可以看作哪两个相邻的“三角形数”之和?
解:是. ∵152=225.
∴225是“正方形数”.
由(5)得, ,
∴225可以看作105,120这两个相邻的“三角形数”之和.
2.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题:
(1)在第n个图中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(n+3)
(n+2)
(2) 按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
解:(2)第n个图共有(n2+5n+6)块瓷砖.
由n2+5n+6=506.
解得n1=20,n2=-25(舍去).∴n=20.
(3) 若黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需花多少元钱购买瓷砖
白瓷砖块数是n(n+1)=20×(20+1)=420,
黑瓷砖块数是506-420=86.
86×4+420×3=1604(元).
共需1604元钱购买瓷砖.
(4) 是否存在黑瓷砖与白瓷砖块数相等的情形 请通过计算说明为什么
在第n个图中白瓷砖块数是n(n+1).
则有n(n+1)=(n2+5n+6)-n(n+1)
化简得n2-3n-6=0
解得n1= , n2= .
∵n为正整数,不合题意.
∴不存在黑瓷砖与白瓷砖块数相等的情形.
课堂小结
三角形点阵前n行数点数和
正六边形第n层所对应的点数(n≥2)
6(n-1)
n层正六边形点阵的总点数(n≥2);
1+3n(n-1)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
数学活动
R·九年级上册
新课导入
导入课题
点是几何中最基本的图形,许多点排列起来可以组成一个点阵.
今天我们就来看看点阵中隐藏了什么有趣的数学规律.
(1)通过观察点阵(数学模型),了解并掌握一些点阵及数学模型的变化规律.
(2)探究三角点阵中前n行的点数和的计算公式.
(3)运用一元二次方程的知识和三角点阵中前n行的点数和的计算公式解决问题.
(4)通过活动,培养学生的观察、比较、归纳和概括能力,培养学生的空间想象能力.
活动目标
推进新课
图1是一个三角形点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点…….
观察图形,完成下面各题.
·
··
···
····
·····
······
·······
……
图 1
活 动 1
三角形点阵
①下表是该点阵前n行的点数和,请你按要求把它填写完整
前n行数 1 2 3 4 5 … 10 … n
点数和
1
3
6
10
15
…
…
55
②若该三角点阵前n行的点数和是300,求行数n.
由①知.前n行的点数和为 ,解得n1=24,n2=-25(舍去),即行数n为24.
③该三角点阵前n行的点数和能是600吗?如果能,求出其行数n;如果不能,请说明理由.
前n行的点数和 ,解得n1= , n2= ,因为n是正整数,方程的两根均不符合条件,所以三角点阵前n行的点数和不能是600.
④如果把图中的三角点阵中各行的点数依次换为2,4,6,…,2n,…,你能探究出前n行的点数和满足什么规律吗?
前n行的点数和为
⑤在④中,三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明理由.
依题意,n(n+1)=600.
解得n1=24,n2=-25(舍去).
活 动 2
正六边形点阵
如图2 是一个形如正六边形的点阵,它的中心是一个点,算作第一层,第二层每边有两个点,第三层每边有三个点,……,依此类推.
图 2
·····
······
·······
········
·········
········
·······
······
·····
①填写下表:
层 数 1 2 3 4 …
该层对应的点数
所有层的总点数
1
6
12
18
…
1
7
19
37
…
②第n层所对应的点数为 (n≥2).
③写出n层正六边形点阵的总点数(n≥2);
6(n-1)
1+6×1+6×2+…+6(n-1)
=1+6·
=1+3n(n-1)
④如果点阵中所有层的总点数为331,请求出它共有几层?
1+3n(n-1)=331
化简方程为:n2-n-110=0
分解因式为:(n-11)(n+10)=0
解得:n1=11,n2=-10(舍去),
所以共有11层.
⑤ 点阵设计大赛:
设计时间:5分钟.
设计要求:
a .每人设计一组有规律、美观的点阵图,画出前4个点阵,并仿照三角形点阵的探究提出问题,然后在小组内交流自己的设计方案.
b.每组评选出优秀作品,派代表说明设计的方法及点阵中的规律.
随堂演练
1. 古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律.
(1)下图反映了一个“三角形数”是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
·
··
···
····
·
··
···
·
··
·
①1=1;
②1+2= ;
③1+2+3= ;
④1+2+3+4= .
3
6
10
(2)通过猜想,写出(1)中与第九个点阵相对应的等式: 。
(3)2015是“三角形数”吗?为什么?
1+2+3+…+9=45
解:不是.“三角形数”都可以写成 的形式,
令2015= ,
解得n1= ,n2= .
因为n是正整数,方程的两根均不符合条件,所以2015不是“三角形”数.
(4)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
··
··
·
···
···
···
····
····
····
····
·····
·····
·····
·····
·····
①1=12; ②1+3=22;
③3+6=32; ④6+10=42;
⑤ .
10+15=52
(5)通过猜想,写出(4)中与第n个点阵相对应的等式: .
(6)判断225是不是“正方形数”,如果不是,说明理由;如果是,225可以看作哪两个相邻的“三角形数”之和?
解:是. ∵152=225.
∴225是“正方形数”.
由(5)得, ,
∴225可以看作105,120这两个相邻的“三角形数”之和.
2.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题:
(1)在第n个图中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(n+3)
(n+2)
(2) 按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
解:(2)第n个图共有(n2+5n+6)块瓷砖.
由n2+5n+6=506.
解得n1=20,n2=-25(舍去).∴n=20.
(3) 若黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需花多少元钱购买瓷砖
白瓷砖块数是n(n+1)=20×(20+1)=420,
黑瓷砖块数是506-420=86.
86×4+420×3=1604(元).
共需1604元钱购买瓷砖.
(4) 是否存在黑瓷砖与白瓷砖块数相等的情形 请通过计算说明为什么
在第n个图中白瓷砖块数是n(n+1).
则有n(n+1)=(n2+5n+6)-n(n+1)
化简得n2-3n-6=0
解得n1= , n2= .
∵n为正整数,不合题意.
∴不存在黑瓷砖与白瓷砖块数相等的情形.
课堂小结
三角形点阵前n行数点数和
正六边形第n层所对应的点数(n≥2)
6(n-1)
n层正六边形点阵的总点数(n≥2);
1+3n(n-1)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
