【高效备课】人教版九(上) 第21章 一元二次方程 章末复习 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 第21章 一元二次方程 章末复习 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:40 | ||
图片预览






文档简介
(共16张PPT)
章末复习
R·九年级上册
新课导入
导入课题
通过对一元二次方程这章的学习,你掌握了哪些知识?这些知识点间又有哪些联系呢?如何运用这些知识解决问题呢?
复习目标
(1)梳理本章的知识结构网络,回顾与复习本章知识.
(2)能选择适当的方法,快速、准确地解一元二次方程,知道一元二次方程根的判别式和一元二次方程根与系数的关系,并能利用它们解决有关问题.
(3)列一元二次方程解决实际问题.
(4)进一步加深对方程思想、分类思想、转化思想(即降次)的理解与运用.
知识积累
a. 一元二次方程的概念,一般形式分别是什么?如何验根?
b. 一元二次方程有哪几种解法?
一般情况下如何选择最优解法?
c. 若一元二次方程ax2+bx+c=0(a≠0)有实数根x1,x2,则其求根
公式是x= .
根与系数的关系是:x1+x2= ,x1x2= .
d.判别一个一元二次方程是否有实根,只需确定 的
符号:
当 时,方程有两个不等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
e.列一元二次方程可以解决许多实际问题,解题的一般步
骤是: .
b2-4ac
b2-4ac>0
b2-4ac=0
b2-4ac<0
审、设、列、解、验、答
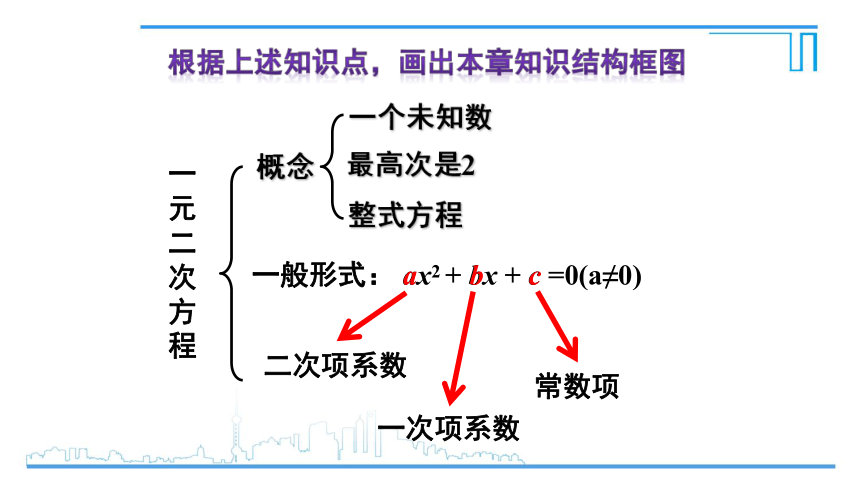
根据上述知识点,画出本章知识结构框图
一般形式: ax2 + bx + c =0(a≠0)
a
b
c
二次项系数
一次项系数
常数项
一元二次方程
概念
一个未知数
最高次是2
整式方程
根
根的判别式Δ=b2-4ac
Δ>0,方程有两个不等的实数根
Δ=0,方程有两个相等的实数根
Δ<0,方程无实数根
根与系数的关系
解法
因式分解法:
配方法:
公式法:
若A·B=0,则A=0或B=0
形如x2=p或(mx+n)2=p(p≥0)的形式直接开平方
一般形式的方程先配方为(mx+n)2=p(p≥0)的形式再求解
应用
列一元二次方程解实际问题的步骤:
审设列解验答
几种常见类型
传播问题
增长率问题
图形面积问题
单(双)循环问题
方案设计问题
数字问题
随堂演练
1.方程(2x+1)(x-3)=x2+1化成一般形式为 ,
二次项系数、一次项系数和常数项分别是 .
2. 用配方法解下列方程,其中应在左右两边同时加上4的
是( )
A.x2-2x=5 B.2x2-4x=5
C.x2+4x=5 D.x2+2x=5
x2-5x-4=0
1,-5,-4
C
3. 一个小组若干人,新年互送贺卡,若全组共送贺卡72
张,则这个小组共有( )
A.12人 B.18人 C.9人 D.10人
4. 某超市一月份的营业额为200万元,一、二、三月份的
总营业额为1000万元,设平均每月营业额的增长率为x,
则由题意列方程为( )
A.200+200×2x=1000 B.200(1+x)2=1000
C.200+200×3x=1000 D.200[1+(1+x)+(1+x)2]=1000
C
D
x2-2x=0; x2-2x+2=0.
解:分解因式得:
x(x-2)=0
x=0或x-2=0
x1=0,x2=2
解:x2-2x+1=-1
(x-1)2=-1
方程无解
5. 解下列方程:
6. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若以每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少
解:设销售单价为x元.则月销售量为[500-10(x-50)]kg.
由题意可得 (x-40)[500-10(x-50)]=8000,
解得 x1=60, x2=80,
又 40[500-10(x-50)]≤10000.
x≥75.
∴x=60<75(舍去)
答:销售单价应为80元.
7. 一个两位数,它的十位数字比个位数字小3,且个 位
数字的平方恰好等于这个两位数,求这个两位数.
解:设十位数字是x,则个位数字是x+3,根据题意,
得(x+3)2=10x+x+3.
整理得x2-5x+6=0,解得x1=2,x2=3.
当x=2时,x+3=5;当x=3时,x+3=6.
∴这个两位数是25或36.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
章末复习
R·九年级上册
新课导入
导入课题
通过对一元二次方程这章的学习,你掌握了哪些知识?这些知识点间又有哪些联系呢?如何运用这些知识解决问题呢?
复习目标
(1)梳理本章的知识结构网络,回顾与复习本章知识.
(2)能选择适当的方法,快速、准确地解一元二次方程,知道一元二次方程根的判别式和一元二次方程根与系数的关系,并能利用它们解决有关问题.
(3)列一元二次方程解决实际问题.
(4)进一步加深对方程思想、分类思想、转化思想(即降次)的理解与运用.
知识积累
a. 一元二次方程的概念,一般形式分别是什么?如何验根?
b. 一元二次方程有哪几种解法?
一般情况下如何选择最优解法?
c. 若一元二次方程ax2+bx+c=0(a≠0)有实数根x1,x2,则其求根
公式是x= .
根与系数的关系是:x1+x2= ,x1x2= .
d.判别一个一元二次方程是否有实根,只需确定 的
符号:
当 时,方程有两个不等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
e.列一元二次方程可以解决许多实际问题,解题的一般步
骤是: .
b2-4ac
b2-4ac>0
b2-4ac=0
b2-4ac<0
审、设、列、解、验、答
根据上述知识点,画出本章知识结构框图
一般形式: ax2 + bx + c =0(a≠0)
a
b
c
二次项系数
一次项系数
常数项
一元二次方程
概念
一个未知数
最高次是2
整式方程
根
根的判别式Δ=b2-4ac
Δ>0,方程有两个不等的实数根
Δ=0,方程有两个相等的实数根
Δ<0,方程无实数根
根与系数的关系
解法
因式分解法:
配方法:
公式法:
若A·B=0,则A=0或B=0
形如x2=p或(mx+n)2=p(p≥0)的形式直接开平方
一般形式的方程先配方为(mx+n)2=p(p≥0)的形式再求解
应用
列一元二次方程解实际问题的步骤:
审设列解验答
几种常见类型
传播问题
增长率问题
图形面积问题
单(双)循环问题
方案设计问题
数字问题
随堂演练
1.方程(2x+1)(x-3)=x2+1化成一般形式为 ,
二次项系数、一次项系数和常数项分别是 .
2. 用配方法解下列方程,其中应在左右两边同时加上4的
是( )
A.x2-2x=5 B.2x2-4x=5
C.x2+4x=5 D.x2+2x=5
x2-5x-4=0
1,-5,-4
C
3. 一个小组若干人,新年互送贺卡,若全组共送贺卡72
张,则这个小组共有( )
A.12人 B.18人 C.9人 D.10人
4. 某超市一月份的营业额为200万元,一、二、三月份的
总营业额为1000万元,设平均每月营业额的增长率为x,
则由题意列方程为( )
A.200+200×2x=1000 B.200(1+x)2=1000
C.200+200×3x=1000 D.200[1+(1+x)+(1+x)2]=1000
C
D
x2-2x=0; x2-2x+2=0.
解:分解因式得:
x(x-2)=0
x=0或x-2=0
x1=0,x2=2
解:x2-2x+1=-1
(x-1)2=-1
方程无解
5. 解下列方程:
6. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若以每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少
解:设销售单价为x元.则月销售量为[500-10(x-50)]kg.
由题意可得 (x-40)[500-10(x-50)]=8000,
解得 x1=60, x2=80,
又 40[500-10(x-50)]≤10000.
x≥75.
∴x=60<75(舍去)
答:销售单价应为80元.
7. 一个两位数,它的十位数字比个位数字小3,且个 位
数字的平方恰好等于这个两位数,求这个两位数.
解:设十位数字是x,则个位数字是x+3,根据题意,
得(x+3)2=10x+x+3.
整理得x2-5x+6=0,解得x1=2,x2=3.
当x=2时,x+3=5;当x=3时,x+3=6.
∴这个两位数是25或36.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
同课章节目录
