【高效备课】人教版九(上) 第23章 旋转 章末复习 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 第23章 旋转 章末复习 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 285.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:40 | ||
图片预览




文档简介
(共17张PPT)
章末复习
R·九年级上册
复习导入
复习导入
本节课将回顾全章所学内容,梳理知识脉络,击破重难点和考点.
学习目标
(1)梳理全章知识要点,能画出它的知识结构框图.
(2)进一步明确旋转、中心对称的概念含义及它们的性质和作图等.
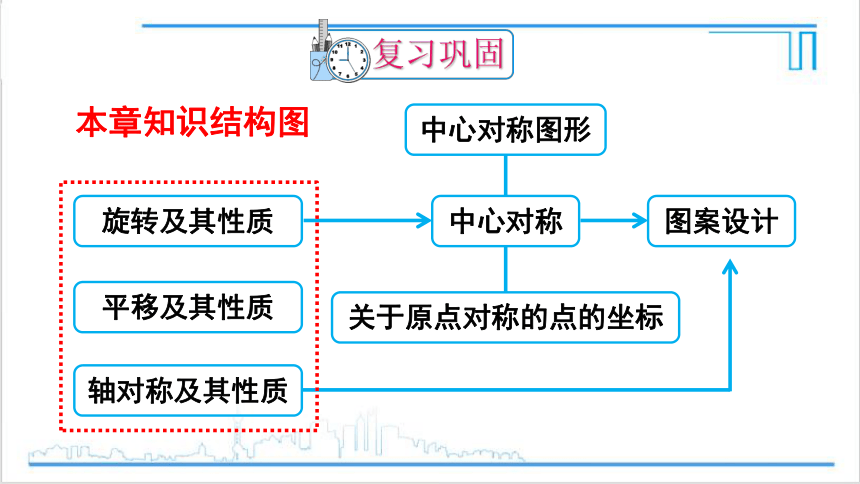
本章知识结构图
旋转及其性质
平移及其性质
轴对称及其性质
中心对称图形
中心对称
关于原点对称的点的坐标
图案设计
复习巩固
梳理知识要点:
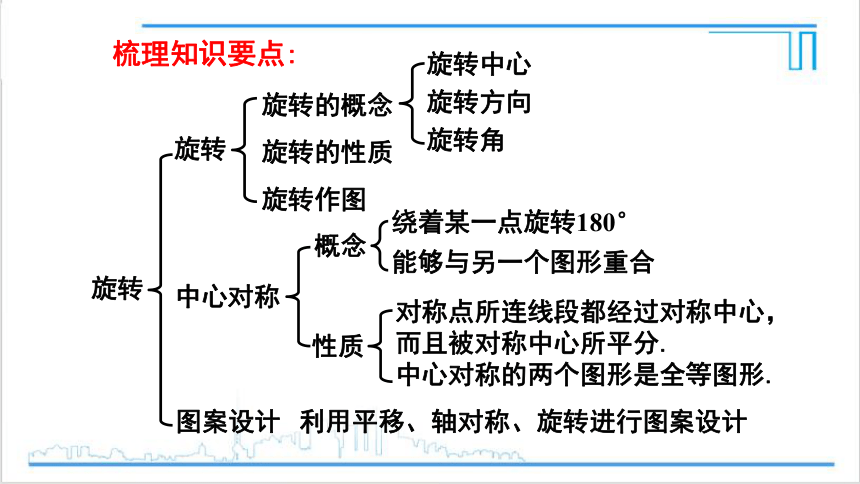
旋转
旋转
旋转的概念
旋转的性质
旋转作图
旋转中心
旋转方向
旋转角
中心对称
概念
性质
绕着某一点旋转180°
能够与另一个图形重合
对称点所连线段都经过对称中心,而且被对称中心所平分.
中心对称的两个图形是全等图形.
图案设计
利用平移、轴对称、旋转进行图案设计
旋转的性质:
对应点到旋转中心的距离相等
对应点与旋转中心连线的夹角等于旋转角
旋转不改变图形的形状和大小
中心对称的性质:
对称点的连线经过对称中心且被对称中心平分
关于对称中心对称的两个图形是全等图形
关于原点对称的两点:
横、纵坐标分别互为相反数
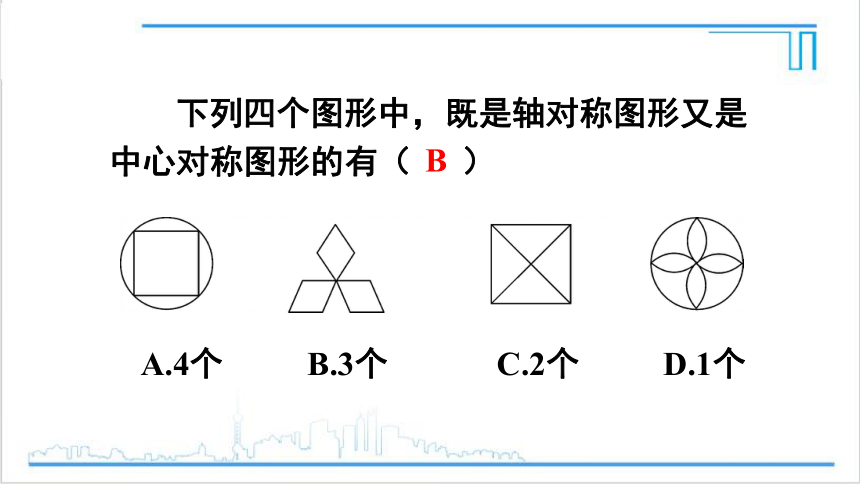
下列四个图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
B
在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以将图形进行以下的操作( )
A.先逆时针旋转90°,再向左平移
B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移
D.先顺时针旋转90°,再向右平移
A
若点A(2m-1,2n+3)与B(2-m,2-n)关于原点O对称,则m=_____, n=_____.
-1
-5
本章主要考点:
(1)中心对称图形的识别(或综合轴对称图形);
(2)关于原点对称的点的坐标的运用;
(3)利用旋转进行相关的计算或证明;
(4)平移、轴对称和旋转变换的综合运用;
(5)中心对称的性质的应用及相关的作图等.
随堂演练
1.如图,将△ABC绕点A逆时针旋转一定角度,得△ADE.
若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数
为( )
A.60° B.75°
C.85° D.90°
2.已知点P(a,a+2)在直线y=2x-1上,
则点P关于原点的对称点P′的坐标为( )
A.(3,5) B(-3,5)
C.(3,-5) D.(-3,-5)
C
D
3.如图,边长为4的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC于E、F两点,则阴影部分的面积是( )
A.1 B.4 C.6 D.8
B
4.如图,写出△ABC三顶点的坐标,并在图中描出点
A1(3,3),B1(2,-2),C1(4,-1),并说明
△A1B1C1是△ABC通过怎样的变化得到的?
解:A(-2,2),B(-1,-2),C(-3,-3). 描点如图.△A1B1C1是由△ABC先向右平移5个单位,再向上平移1个单位得到的.
平行四边形
5.如图,平行四边形ABCD中,AB⊥AC,AB=2,BC=2 ,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC、AD于点F、E.
(1)当旋转角度为90°时,四边形
ABFE的形状是___________;
(2)试说明在旋转过程中,线段AF与EC总是保持相等;
(3)在旋转过程中四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由,并求出此时AC绕点O顺时针旋转的度数.
解:(2)连接AF, EC.
∵四边形ABCD是平行四边形.
∴AD与CB关于点O中心对称.
又E、F分别在上.
∴AE与CF关于点O中心对称.
∴AE=CF,又AE∥CF,
∴四边形AFCE是平行四边形.
∴AF=CE.
(3)可能是菱形,当AC绕点O旋转45°时,
∵AC= =4,
∴OA=OC=2,∴OA=AB,又∠BAC=90°,
∴△OAB为等腰直角三角形,∠AOB=45°.
当AC绕点O顺时针旋转45°时,
∠AOE=45°,∴∠BOE=90°,
∴EF垂直平分BD,∴BE=ED.
又由(1)可知四边形BEDF为平行四边形,
即此时四边形BEDF是菱形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
章末复习
R·九年级上册
复习导入
复习导入
本节课将回顾全章所学内容,梳理知识脉络,击破重难点和考点.
学习目标
(1)梳理全章知识要点,能画出它的知识结构框图.
(2)进一步明确旋转、中心对称的概念含义及它们的性质和作图等.
本章知识结构图
旋转及其性质
平移及其性质
轴对称及其性质
中心对称图形
中心对称
关于原点对称的点的坐标
图案设计
复习巩固
梳理知识要点:
旋转
旋转
旋转的概念
旋转的性质
旋转作图
旋转中心
旋转方向
旋转角
中心对称
概念
性质
绕着某一点旋转180°
能够与另一个图形重合
对称点所连线段都经过对称中心,而且被对称中心所平分.
中心对称的两个图形是全等图形.
图案设计
利用平移、轴对称、旋转进行图案设计
旋转的性质:
对应点到旋转中心的距离相等
对应点与旋转中心连线的夹角等于旋转角
旋转不改变图形的形状和大小
中心对称的性质:
对称点的连线经过对称中心且被对称中心平分
关于对称中心对称的两个图形是全等图形
关于原点对称的两点:
横、纵坐标分别互为相反数
下列四个图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
B
在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以将图形进行以下的操作( )
A.先逆时针旋转90°,再向左平移
B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移
D.先顺时针旋转90°,再向右平移
A
若点A(2m-1,2n+3)与B(2-m,2-n)关于原点O对称,则m=_____, n=_____.
-1
-5
本章主要考点:
(1)中心对称图形的识别(或综合轴对称图形);
(2)关于原点对称的点的坐标的运用;
(3)利用旋转进行相关的计算或证明;
(4)平移、轴对称和旋转变换的综合运用;
(5)中心对称的性质的应用及相关的作图等.
随堂演练
1.如图,将△ABC绕点A逆时针旋转一定角度,得△ADE.
若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数
为( )
A.60° B.75°
C.85° D.90°
2.已知点P(a,a+2)在直线y=2x-1上,
则点P关于原点的对称点P′的坐标为( )
A.(3,5) B(-3,5)
C.(3,-5) D.(-3,-5)
C
D
3.如图,边长为4的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC于E、F两点,则阴影部分的面积是( )
A.1 B.4 C.6 D.8
B
4.如图,写出△ABC三顶点的坐标,并在图中描出点
A1(3,3),B1(2,-2),C1(4,-1),并说明
△A1B1C1是△ABC通过怎样的变化得到的?
解:A(-2,2),B(-1,-2),C(-3,-3). 描点如图.△A1B1C1是由△ABC先向右平移5个单位,再向上平移1个单位得到的.
平行四边形
5.如图,平行四边形ABCD中,AB⊥AC,AB=2,BC=2 ,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC、AD于点F、E.
(1)当旋转角度为90°时,四边形
ABFE的形状是___________;
(2)试说明在旋转过程中,线段AF与EC总是保持相等;
(3)在旋转过程中四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由,并求出此时AC绕点O顺时针旋转的度数.
解:(2)连接AF, EC.
∵四边形ABCD是平行四边形.
∴AD与CB关于点O中心对称.
又E、F分别在上.
∴AE与CF关于点O中心对称.
∴AE=CF,又AE∥CF,
∴四边形AFCE是平行四边形.
∴AF=CE.
(3)可能是菱形,当AC绕点O旋转45°时,
∵AC= =4,
∴OA=OC=2,∴OA=AB,又∠BAC=90°,
∴△OAB为等腰直角三角形,∠AOB=45°.
当AC绕点O顺时针旋转45°时,
∠AOE=45°,∴∠BOE=90°,
∴EF垂直平分BD,∴BE=ED.
又由(1)可知四边形BEDF为平行四边形,
即此时四边形BEDF是菱形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
