【高效备课】人教版九(上) 第24章 圆 数学活动 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 第24章 圆 数学活动 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:40 | ||
图片预览







文档简介
(共36张PPT)
数学活动
R·九年级上册
新课导入
日常生活中同学们经常见到的汽车、摩托车、自行车等一些交通运输工具的车轮是什么形状的?请同学们思考一个问题,为什么车轮要做成圆形呢?能否做成长方形或正方形?
(1)通过活动理解车轮做成圆形的数学道理.
(2)探究能过四边形的四个顶点作圆的条件.
(3)以圆和正多边形为基本图形设计图案.
推进新课
活动1
车轮做成圆形的数学道理
现代
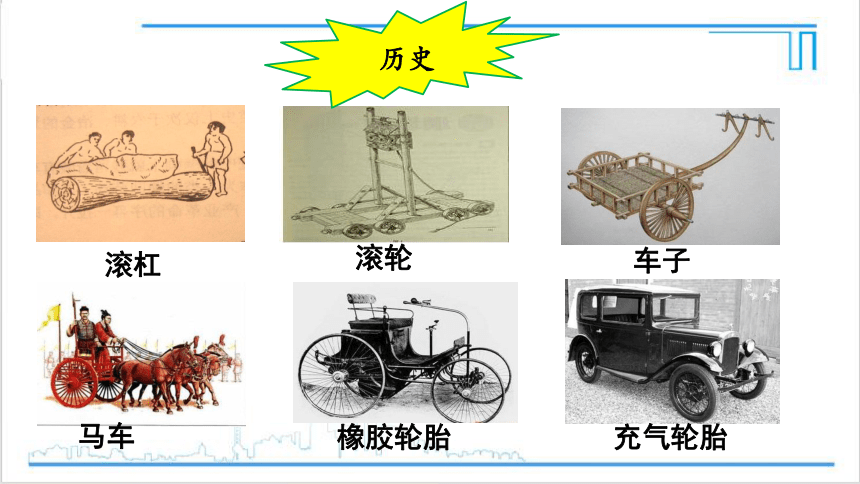
滚杠
滚轮
车子
马车
橡胶轮胎
充气轮胎
历史
通过这场比赛,你发现什么问题?
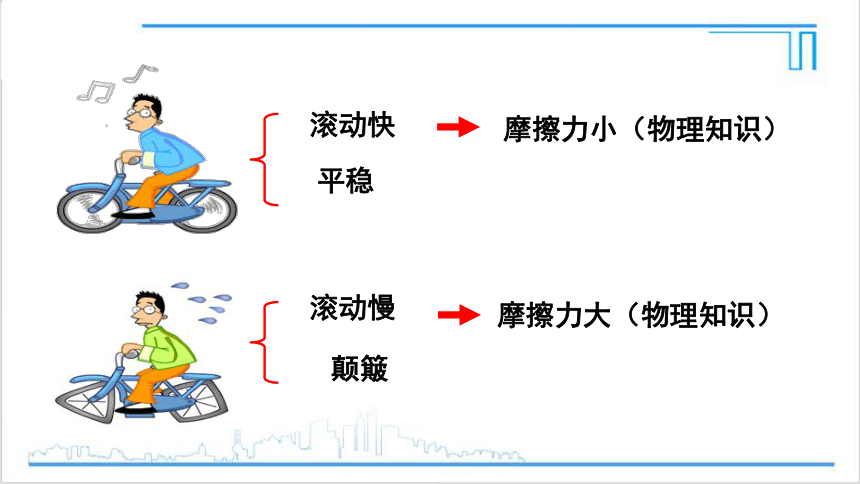
滚动快
平稳
滚动慢
颠簸
摩擦力小(物理知识)
摩擦力大(物理知识)
(1)车轮在滚动的过程中圆上各点有什么特点?
为什么车轮做成圆形会更平稳?
(2)车轮在滚动的过程中什么没有变?
A
B
C
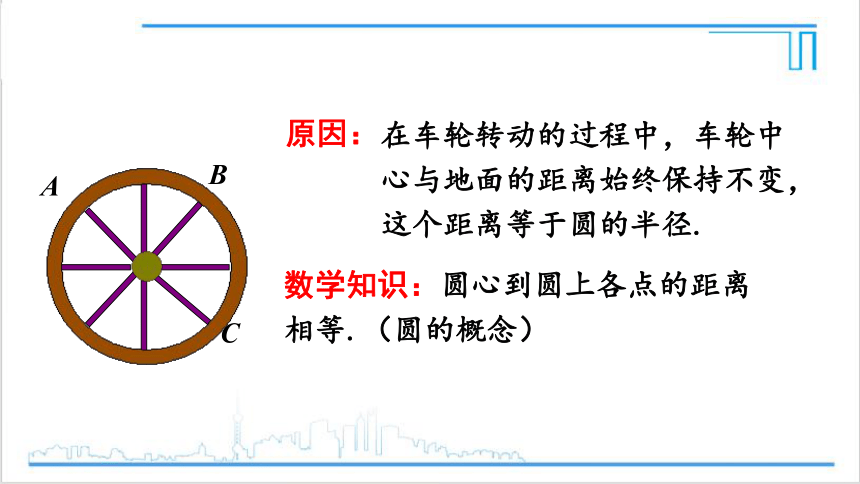
在车轮转动的过程中,车轮中心与地面的距离始终保持不变,这个距离等于圆的半径.
数学知识:圆心到圆上各点的距离相等.(圆的概念)
原因:
A
B
C
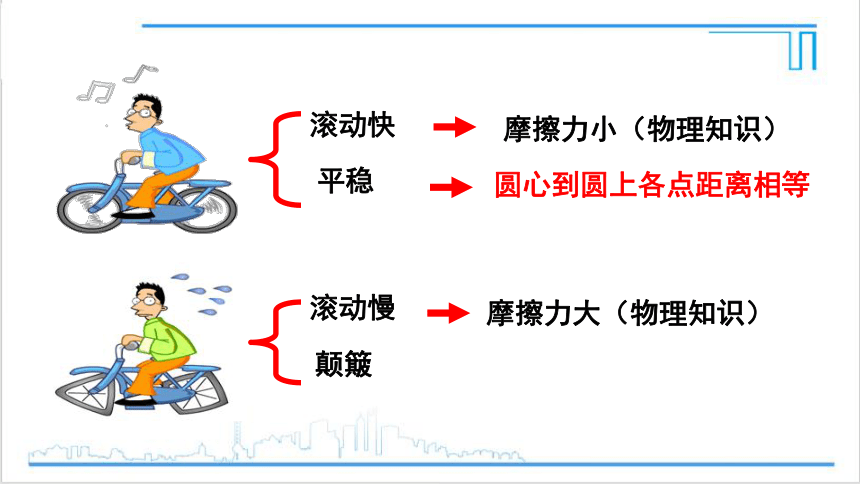
滚动快
平稳
滚动慢
摩擦力小(物理知识)
摩擦力大(物理知识)
颠簸
圆心到圆上各点距离相等
如果车轮是正方形形状,请尝试画出它中心点的运动轨迹.
如果车轮是正三角形,它中心点的运动轨迹又会怎么样呢?
为什么三角形或正方形车轮会出现颠簸?
为什么三角形或正方形车轮会出现颠簸?
滚动快
平稳
滚动慢
摩擦力小(物理知识)
摩擦力大(物理知识)
颠簸
圆心到圆上各点距离相等
中心的轨迹不是一条直线
车轮做成圆形的数学道理
圆心到圆上各点的距离相等
你还想知道车轮做成圆形其他的道理吗?
课后相互讨论查阅资料完成
我们知道:过任意一个三角形的三个顶点一定能作一个圆,过四边形的四个顶点一定能作一个圆吗?
活动2
探究四点共圆的条件
不一定
A
B
C
D
1.四点在同一条直线上不能作圆.
四点中任意三点不在一条直线上,不一定作圆.
A
B
C
D
A
B
C
D
A
B
C
D
2.三点在同一条直线上, 另一点不在这条直线上不能作圆.
举 例
图中给出了一些四边形,能否过它们的四个顶点作一个圆?试一试!
A
B
C
D
A
B
C
D
A
B
C
D
试一试
×
分别测量上面各四边形的内角,如果过某个四边形的四个顶点能作一个圆,那么其相对的两个内角之间有什么关系?证明你的发现.
∠A+∠C=180°
∠B+∠D=180°
发现:过某个四边形的四个顶点能作一个圆,那么其相对的两个内角之和为180°.
A
B
C
D
A
B
C
D
测量
∵四边形ABCD是⊙O的内接四边形.
∴弧BAD和弧BCD的圆心角的和是周角.
同理
所以圆内接四边形的相对两角之和为180°.
B
C
D
A
·
O
证明:
如果过某个四边形的四个顶点不能作一个圆,那么其两个相对的内角之间有上面的关系吗?
·
A
B
C
D
O
其相对的两个内角之和不等于180°.
·
A
B
C
D
E
F
O
试结合图说明其中的道理.
探究
有
·
A
B
C
D
O
连接AC并延长交⊙O于点C ,连接BC 和DC .
C
又∵点C'在⊙O上,
∴∠A+∠BCD>∠BC′D+∠A
说明
情况一
由上面的探究,试归纳出判断过某个四边形的四个顶点能作一个圆的条件.
连接AC交⊙O与点C',连接BC'和DC'.
·
A
B
C
D
E
F
O
C
有
所以
又因为点C′在⊙O上,
所以∠A+∠BC′D>∠BCD + ∠A.
情况二
四边形相对的两个内角互补,四点共圆.
四点共圆的条件
许多图案设计都和圆有关,图1就是利用等分圆周设计出的一些图案,图2展示了一朵雏菊图案的设计过程.
图2
活动3
设计图案
利用正多边形可以镶嵌整个平面的性质,还可以设计出一些美丽的图案,如图.
你能画出其中的一些图案吗?请你再利用圆或正多边形设计一些图案,并与同学交流.
随堂演练
基础巩固
1.四边形ABCD内接于⊙O,∠A∶∠B∶∠C=7
∶6∶3,则∠D等于( )
A.36° B.72° C.144° D.54°
B
2.下列美妙的图案中,是由正三角形、正方
形、正六边形、正八边形中的三种镶嵌而成的为( )
D
3.现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式有( )
A.2种 B.3种 C.4种 D.5种
B
4. 如图(1)是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图(2)所示,四边形ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇
形,得到如图所示的扇
环形,图(1)中的圆与扇
环的面积比为 .
4∶9
5.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为 cm.
4π
6.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA,OB,OC,OD
的中点,若⊙O的半径为2,则阴影部分的面积
为 .
8
7.如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为 .
2π-4
8. 如图,在△ABC中, AD⊥BC, DE⊥AB, DF⊥AC. 求证: B、E、F、C四点共圆.
综合应用
证明:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∴∠AED+AFD=180°.
∴A、E、D、F四点共圆.
∴∠DEF=∠DAF.又AD⊥DC,
∴∠DAF+∠C=90°.
∴∠DEF+∠C=90°.
∴∠BEF+∠C=∠BED+∠DEF+∠C=180°.
∴B、E、F、C四点共圆.
9.如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.
证明:连接OE、OF、OG、OH.
∵四边形ABCD是菱形,∴AC⊥BD.
又∵E、F、G、H分别是菱形ABCD的各边中点,
∴OE=OF=OG=OH= AB= BC= CD= DA.
∴E、F、G、H四点共圆.
拓展延伸
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
数学活动
R·九年级上册
新课导入
日常生活中同学们经常见到的汽车、摩托车、自行车等一些交通运输工具的车轮是什么形状的?请同学们思考一个问题,为什么车轮要做成圆形呢?能否做成长方形或正方形?
(1)通过活动理解车轮做成圆形的数学道理.
(2)探究能过四边形的四个顶点作圆的条件.
(3)以圆和正多边形为基本图形设计图案.
推进新课
活动1
车轮做成圆形的数学道理
现代
滚杠
滚轮
车子
马车
橡胶轮胎
充气轮胎
历史
通过这场比赛,你发现什么问题?
滚动快
平稳
滚动慢
颠簸
摩擦力小(物理知识)
摩擦力大(物理知识)
(1)车轮在滚动的过程中圆上各点有什么特点?
为什么车轮做成圆形会更平稳?
(2)车轮在滚动的过程中什么没有变?
A
B
C
在车轮转动的过程中,车轮中心与地面的距离始终保持不变,这个距离等于圆的半径.
数学知识:圆心到圆上各点的距离相等.(圆的概念)
原因:
A
B
C
滚动快
平稳
滚动慢
摩擦力小(物理知识)
摩擦力大(物理知识)
颠簸
圆心到圆上各点距离相等
如果车轮是正方形形状,请尝试画出它中心点的运动轨迹.
如果车轮是正三角形,它中心点的运动轨迹又会怎么样呢?
为什么三角形或正方形车轮会出现颠簸?
为什么三角形或正方形车轮会出现颠簸?
滚动快
平稳
滚动慢
摩擦力小(物理知识)
摩擦力大(物理知识)
颠簸
圆心到圆上各点距离相等
中心的轨迹不是一条直线
车轮做成圆形的数学道理
圆心到圆上各点的距离相等
你还想知道车轮做成圆形其他的道理吗?
课后相互讨论查阅资料完成
我们知道:过任意一个三角形的三个顶点一定能作一个圆,过四边形的四个顶点一定能作一个圆吗?
活动2
探究四点共圆的条件
不一定
A
B
C
D
1.四点在同一条直线上不能作圆.
四点中任意三点不在一条直线上,不一定作圆.
A
B
C
D
A
B
C
D
A
B
C
D
2.三点在同一条直线上, 另一点不在这条直线上不能作圆.
举 例
图中给出了一些四边形,能否过它们的四个顶点作一个圆?试一试!
A
B
C
D
A
B
C
D
A
B
C
D
试一试
×
分别测量上面各四边形的内角,如果过某个四边形的四个顶点能作一个圆,那么其相对的两个内角之间有什么关系?证明你的发现.
∠A+∠C=180°
∠B+∠D=180°
发现:过某个四边形的四个顶点能作一个圆,那么其相对的两个内角之和为180°.
A
B
C
D
A
B
C
D
测量
∵四边形ABCD是⊙O的内接四边形.
∴弧BAD和弧BCD的圆心角的和是周角.
同理
所以圆内接四边形的相对两角之和为180°.
B
C
D
A
·
O
证明:
如果过某个四边形的四个顶点不能作一个圆,那么其两个相对的内角之间有上面的关系吗?
·
A
B
C
D
O
其相对的两个内角之和不等于180°.
·
A
B
C
D
E
F
O
试结合图说明其中的道理.
探究
有
·
A
B
C
D
O
连接AC并延长交⊙O于点C ,连接BC 和DC .
C
又∵点C'在⊙O上,
∴∠A+∠BCD>∠BC′D+∠A
说明
情况一
由上面的探究,试归纳出判断过某个四边形的四个顶点能作一个圆的条件.
连接AC交⊙O与点C',连接BC'和DC'.
·
A
B
C
D
E
F
O
C
有
所以
又因为点C′在⊙O上,
所以∠A+∠BC′D>∠BCD + ∠A.
情况二
四边形相对的两个内角互补,四点共圆.
四点共圆的条件
许多图案设计都和圆有关,图1就是利用等分圆周设计出的一些图案,图2展示了一朵雏菊图案的设计过程.
图2
活动3
设计图案
利用正多边形可以镶嵌整个平面的性质,还可以设计出一些美丽的图案,如图.
你能画出其中的一些图案吗?请你再利用圆或正多边形设计一些图案,并与同学交流.
随堂演练
基础巩固
1.四边形ABCD内接于⊙O,∠A∶∠B∶∠C=7
∶6∶3,则∠D等于( )
A.36° B.72° C.144° D.54°
B
2.下列美妙的图案中,是由正三角形、正方
形、正六边形、正八边形中的三种镶嵌而成的为( )
D
3.现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式有( )
A.2种 B.3种 C.4种 D.5种
B
4. 如图(1)是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图(2)所示,四边形ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇
形,得到如图所示的扇
环形,图(1)中的圆与扇
环的面积比为 .
4∶9
5.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为 cm.
4π
6.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA,OB,OC,OD
的中点,若⊙O的半径为2,则阴影部分的面积
为 .
8
7.如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为 .
2π-4
8. 如图,在△ABC中, AD⊥BC, DE⊥AB, DF⊥AC. 求证: B、E、F、C四点共圆.
综合应用
证明:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∴∠AED+AFD=180°.
∴A、E、D、F四点共圆.
∴∠DEF=∠DAF.又AD⊥DC,
∴∠DAF+∠C=90°.
∴∠DEF+∠C=90°.
∴∠BEF+∠C=∠BED+∠DEF+∠C=180°.
∴B、E、F、C四点共圆.
9.如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.
证明:连接OE、OF、OG、OH.
∵四边形ABCD是菱形,∴AC⊥BD.
又∵E、F、G、H分别是菱形ABCD的各边中点,
∴OE=OF=OG=OH= AB= BC= CD= DA.
∴E、F、G、H四点共圆.
拓展延伸
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
