【高效备课】人教版九(上) 第24章 圆 复习题24 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 第24章 圆 复习题24 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:40 | ||
图片预览



文档简介
(共27张PPT)
复习题 24
R·九年级上册
复习巩固
1.选择题.
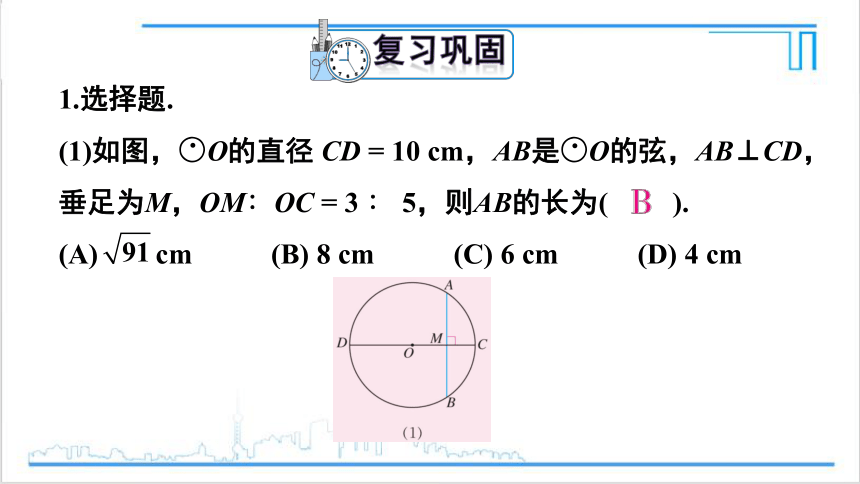
(1)如图,○O的直径 CD = 10 cm,AB是○O的弦,AB⊥CD,垂足为M,OM∶OC = 3 ∶ 5,则AB的长为( ).
(A) cm (B) 8 cm (C) 6 cm (D) 4 cm
·
·
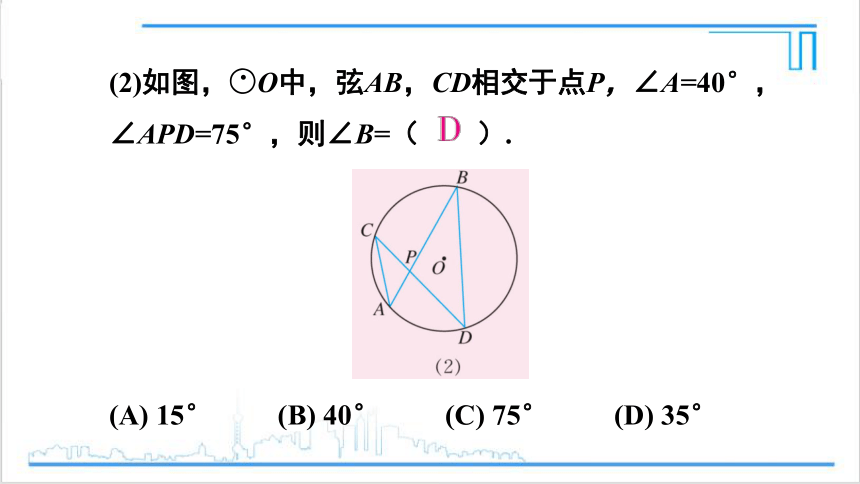
(2)如图,○O中,弦AB,CD相交于点P,∠A=40°,∠APD=75°,则∠B=( ).
·
(A) 15° (B) 40° (C) 75° (D) 35°
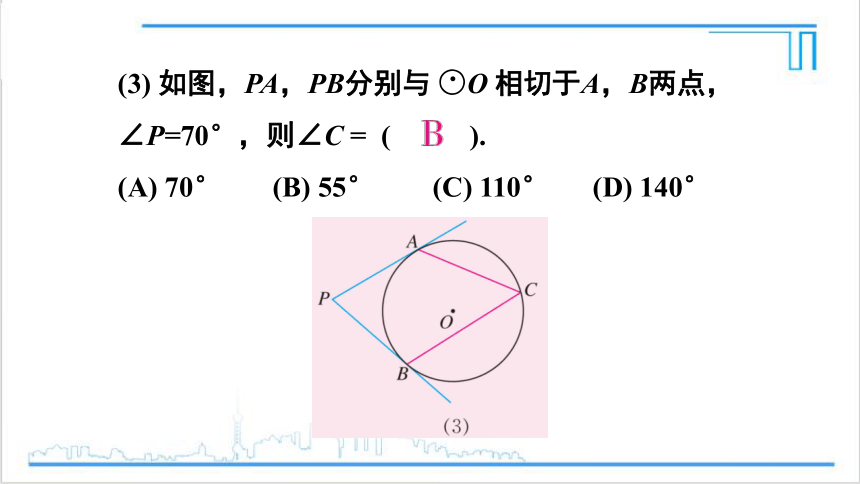
(3) 如图,PA,PB分别与 ○O 相切于A,B两点,∠P=70°,则∠C = ( ).
(A) 70° (B) 55° (C) 110° (D) 140°
·
(4) 以半径为 1 的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( ).
(A)不能构成三角形
(B)这个三角形是等腰三角形
(C)这个三角形是直角三角形
(D)这个三角形是钝角三角形
(5) 一个圆锥的侧面积是底面积的 2 倍,则圆锥侧面展开图的扇形的圆心角是( ).
(A) 120° (B) 180° (C) 240° (D) 300°
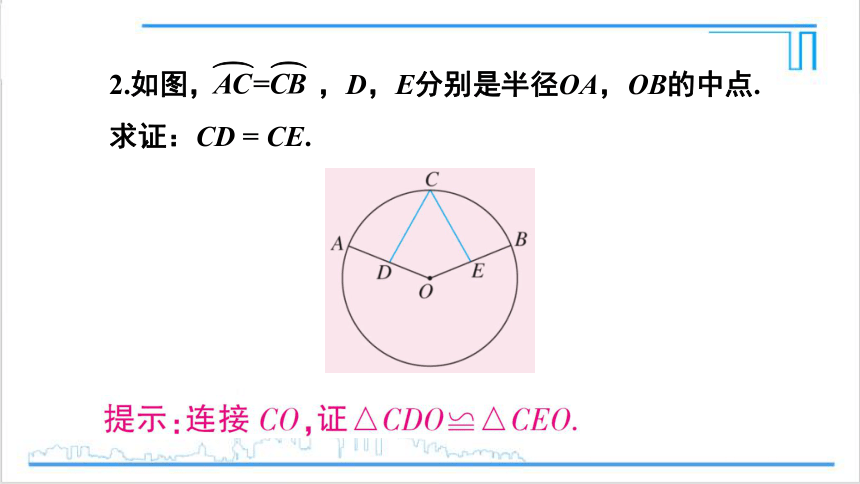
2.如图, ,D,E分别是半径OA,OB的中点.
求证:CD = CE.
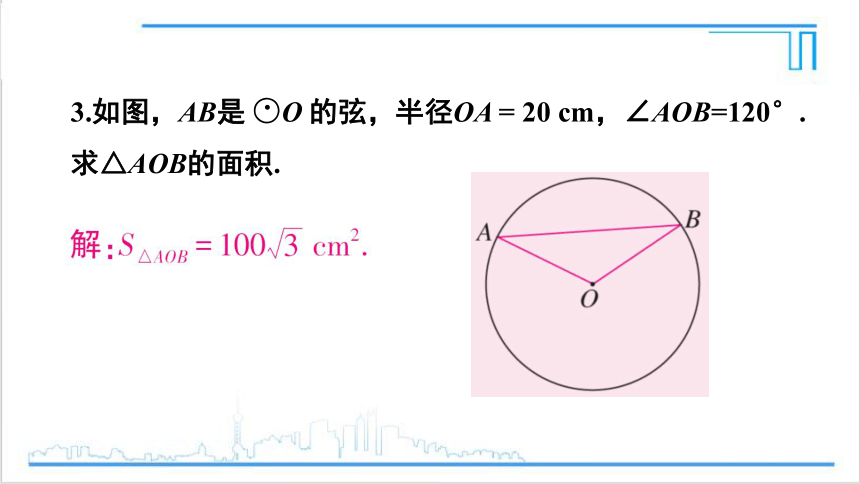
3.如图,AB是 ○O 的弦,半径OA = 20 cm,∠AOB=120°.求△AOB的面积.
·
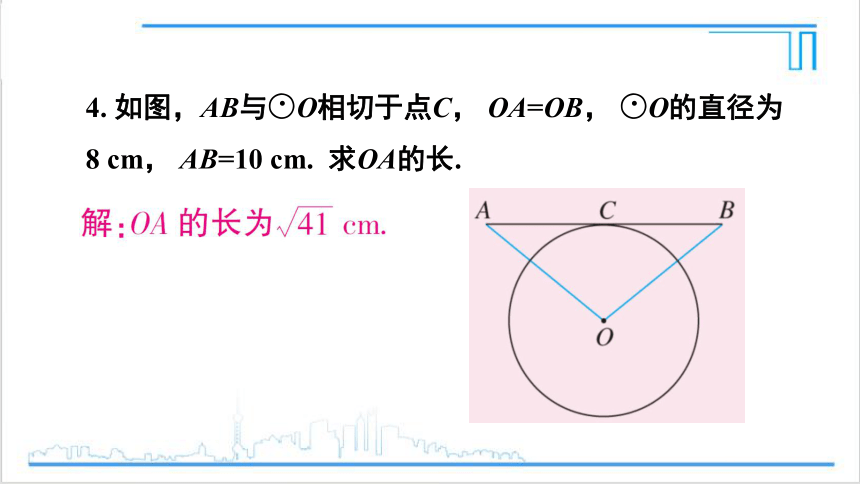
4. 如图,AB与○O相切于点C, OA=OB, ○O的直径为8 cm, AB=10 cm. 求OA的长.
·
·
5.如图,正六边形 ABCDEF 的中心为原点O,顶点A,D在 x 轴上,半径为2 cm,求其各个顶点的坐标。
6. 如图,大半圆中有 n 个小半圆,大半圆的弧长为L1, n个小半圆的弧长和为L2,探索L1和L2的关系并证明你的结论.
7. 如图, ○A, ○B, ○C两两不相交,且半径都是0.5 cm. 求图中三个扇形(即阴影部分)的面积之和。
·
·
·
8. 估计下页图中三段弧的半径的大小关系,再用圆规检验你的结论.
综合运用
9.如图,菱形ABCD的对角线AC,BD相交于点O,四条边AB,BC,CD,DA的中点分别为E,F,G,H. 这四个点共圆吗?圆心在哪里?
10. 往直径为650 mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB = 600 mm,求油的最大深度.
11. 如图,在足球比赛中,甲带球奔向对方球门PQ,当他带球冲到点A时,同伴乙已经冲到点B,此时甲是直接射门好,还是将球传给乙,让乙射门好? (仅从射门角度大小考虑)
12.如图,利用刻度尺和三角尺可以测量圆形工件的直径,说明其中的道理.
13.如图,点 E 是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D. 求证:DE = DB.
14. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:1mm).电镀时,如果每平方米用锌 0.11 kg,电镀100个这样的锚标浮筒,需要用多少锌
15.如图, ○O 的直径AB=12 cm,AM和BN是它的两条切线,DE与 ○O 相切于点E,并与AM,BN分别相交于D,C 两点. 设AD=x,BC=y,求 y 关于 x 的函数解析式,并试着画出它的图象.
拓广探索
·
·
16. 如图,等腰三角形ABC的顶角∠A=36°. ○O和底边BC相切于BC的中点D,并与两腰AC,AB分别相交于E,F,G,H四点,其中G,F分别是两腰AB, AC的中点.求证:五边形DEFGH是正五边形.
·
复习题 24
R·九年级上册
复习巩固
1.选择题.
(1)如图,○O的直径 CD = 10 cm,AB是○O的弦,AB⊥CD,垂足为M,OM∶OC = 3 ∶ 5,则AB的长为( ).
(A) cm (B) 8 cm (C) 6 cm (D) 4 cm
·
·
(2)如图,○O中,弦AB,CD相交于点P,∠A=40°,∠APD=75°,则∠B=( ).
·
(A) 15° (B) 40° (C) 75° (D) 35°
(3) 如图,PA,PB分别与 ○O 相切于A,B两点,∠P=70°,则∠C = ( ).
(A) 70° (B) 55° (C) 110° (D) 140°
·
(4) 以半径为 1 的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( ).
(A)不能构成三角形
(B)这个三角形是等腰三角形
(C)这个三角形是直角三角形
(D)这个三角形是钝角三角形
(5) 一个圆锥的侧面积是底面积的 2 倍,则圆锥侧面展开图的扇形的圆心角是( ).
(A) 120° (B) 180° (C) 240° (D) 300°
2.如图, ,D,E分别是半径OA,OB的中点.
求证:CD = CE.
3.如图,AB是 ○O 的弦,半径OA = 20 cm,∠AOB=120°.求△AOB的面积.
·
4. 如图,AB与○O相切于点C, OA=OB, ○O的直径为8 cm, AB=10 cm. 求OA的长.
·
·
5.如图,正六边形 ABCDEF 的中心为原点O,顶点A,D在 x 轴上,半径为2 cm,求其各个顶点的坐标。
6. 如图,大半圆中有 n 个小半圆,大半圆的弧长为L1, n个小半圆的弧长和为L2,探索L1和L2的关系并证明你的结论.
7. 如图, ○A, ○B, ○C两两不相交,且半径都是0.5 cm. 求图中三个扇形(即阴影部分)的面积之和。
·
·
·
8. 估计下页图中三段弧的半径的大小关系,再用圆规检验你的结论.
综合运用
9.如图,菱形ABCD的对角线AC,BD相交于点O,四条边AB,BC,CD,DA的中点分别为E,F,G,H. 这四个点共圆吗?圆心在哪里?
10. 往直径为650 mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB = 600 mm,求油的最大深度.
11. 如图,在足球比赛中,甲带球奔向对方球门PQ,当他带球冲到点A时,同伴乙已经冲到点B,此时甲是直接射门好,还是将球传给乙,让乙射门好? (仅从射门角度大小考虑)
12.如图,利用刻度尺和三角尺可以测量圆形工件的直径,说明其中的道理.
13.如图,点 E 是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D. 求证:DE = DB.
14. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:1mm).电镀时,如果每平方米用锌 0.11 kg,电镀100个这样的锚标浮筒,需要用多少锌
15.如图, ○O 的直径AB=12 cm,AM和BN是它的两条切线,DE与 ○O 相切于点E,并与AM,BN分别相交于D,C 两点. 设AD=x,BC=y,求 y 关于 x 的函数解析式,并试着画出它的图象.
拓广探索
·
·
16. 如图,等腰三角形ABC的顶角∠A=36°. ○O和底边BC相切于BC的中点D,并与两腰AC,AB分别相交于E,F,G,H四点,其中G,F分别是两腰AB, AC的中点.求证:五边形DEFGH是正五边形.
·
同课章节目录
