【高效备课】人教版九(上) 第24章 圆 章末复习 课件
文档属性
| 名称 | 【高效备课】人教版九(上) 第24章 圆 章末复习 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 15:28:40 | ||
图片预览






文档简介
(共28张PPT)
章末复习
R·九年级上册
复习导入
本节课对全章的知识作一回顾,梳理其知识脉络,熟悉其知识构架,进一步澄清易混点,易错点,同时对本章中的一些常用辅助线和常见分类作一整理.
(1)梳理全章知识点,能画出它的知识结构框图.
(2)总结解题方法,提升解题能力.
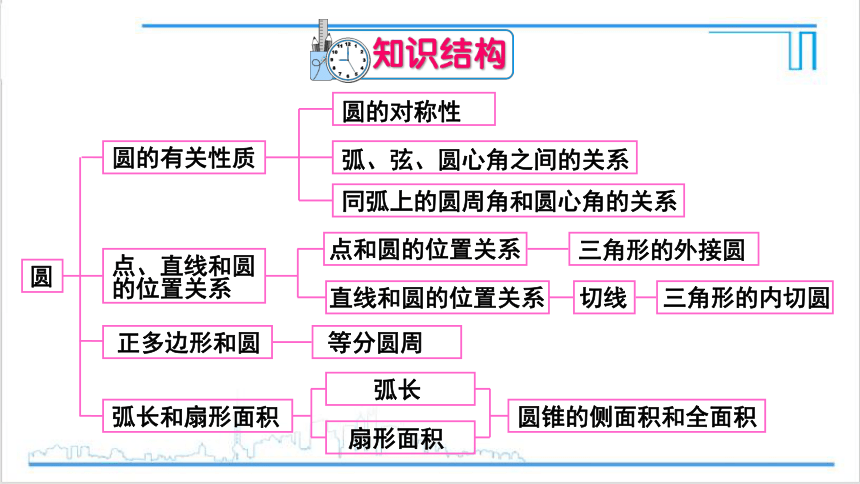
知识结构
圆
圆的有关性质
圆的对称性
弧、弦、圆心角之间的关系
同弧上的圆周角和圆心角的关系
点、直线和圆
的位置关系
正多边形和圆
弧长和扇形面积
扇形面积
弧长
等分圆周
圆锥的侧面积和全面积
点和圆的位置关系
直线和圆的位置关系
切线
三角形的内切圆
三角形的外接圆
在本章,我们利用圆的对称性,探索了圆的一些重要性质;通过图形的运动,研究了点和圆、直线和圆、圆和圆的位置关系;同时研究了圆中的有关计算问题.
重点知识内容
1.
知识回顾
在同圆或等圆中, 相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距也相等.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
(1)在同圆或等圆中的弧、弦、圆心角有什么关系?
2.
·
O
A
B
A′
B′
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦(不是直径)所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
(4)圆的两条平行弦所夹的弧相等.
(2) 垂直于弦的直径有什么性质?
·
O
A
B
C
D
E
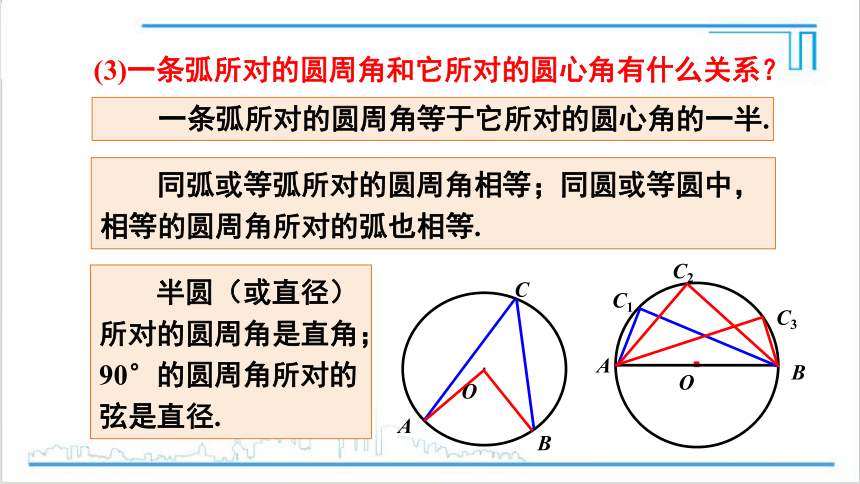
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
(3)一条弧所对的圆周角和它所对的圆心角有什么关系?
·
A
C1
O
C2
C3
B
·
A
C
B
O
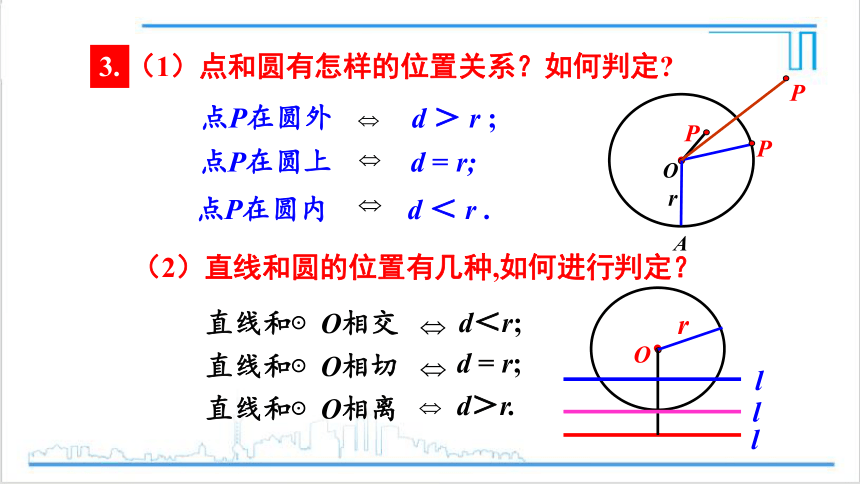
点P在圆内 d < r .
点P在圆外 d > r ;
点P在圆上 d = r;
直线和⊙O相交
直线和⊙O相切
直线和⊙O相离
d<r;
d = r;
d>r.
(1)点和圆有怎样的位置关系?如何判定
(2)直线和圆的位置有几种,如何进行判定?
3.
r
·
O
A
P
P
P
·
l
O
r
l
l
d > r1+r2;
两圆外离
d = r1- r2;
两圆内切
d = r1+r2;
两圆外切
d< r1- r2.
两圆内含
r1-r2<d<r1+r2;
两圆相交
(3)圆和圆的位置关系有几种 如何判定
·
·
O2
O1
·
·
O1
O2
·
·
O1
O2
·
·
O1
O2
·
·
O2
O1
·
O
A
·
O
l
A
(1)圆的切线有什么性质?
圆的切线垂直于过切点的半径.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)如何判断一条直线是圆的切线?
4.
l
正多边形必有外接圆和内切圆.
(1)正多边形和圆有什么关系?
5.
(2) 你能用正多边形和等分圆周设计一些图案吗?
(1)举例说明如何计算弧长?
6.
·
O
n°
1°
1°的圆心角所对的弧长:
n°的圆心角所对的弧长:
(2)举例说明如何计算扇形面积.
1°圆心角的扇形面积:
n°圆心角的扇形的面积:
·
O
n°
则圆锥的侧面积为
圆锥的侧面展开图是一个扇形,设圆锥的母线长为l,底面圆的半径为r.
l
o
r
圆锥的全面积为
(3) 举例说明如何计算圆锥的侧面积和全面积.
随堂演练
基础巩固
1.如图,在⊙O中,弦AB,CD相交于点P,∠A=40°,∠APD=75°,则∠B等于( )
A.15° B.40° C.75° D.35°
D
2.如图,PA,PB分别切⊙O于点A,B,∠P=70°,则∠C=( )
A.70° B.55° C.110° D.140°
B
3.以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )
不能构成三角形
B. 这个三角形是等腰三角形
C. 这个三角形是直角三角形
D. 这个三角形是钝角三角形
C
4.一个圆锥的侧面积是底面积的 倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.180°
C.240° D.300°
C
5.如图所示,P是⊙O外一点,PA、PB分别和⊙O切于点A、B,点C是AB上任意一点,过点C作⊙O的切线分别交PA、PB于点D、E,若△PDE的周长为12,则PA的长为 .
6
⌒
6.如图,AC=CB,D,E分别是半径OA,OB的中点.求证:CD=CE.
证明:连接OC.
∵AC=CB,∴∠COD=∠COE.
∵D、E分别是半径OA、OB的中点,
∴OD=OE= OA= OB.
又OC=OC,
∴△COD≌△COE.∴CD=CE.
⌒
⌒
⌒
⌒
7.在直径为650mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB=600mm,求油的最大深度.
解:过O作OD⊥AB,交AB于点C,交⊙O于点D.
则AC= AB=300mm.
连接OA.设CD=xmm,则OC=(325-x)mm.
在Rt△AOC中,OC2+AC2=OA2,
即(325-x)2+3002=3252.解得x=200.
即CD=200mm.
答:油的最大深度为200mm.
8.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB.
证明:连接OC.
∵OA=OC,∴∠OAC=∠OCA.
又∵DC是⊙O的切线, ∴OC⊥CD.
又AD⊥CD,∴AD∥CO.
∴∠DAC=∠OCA,∴∠DAC=∠OAC.
∴AC平分∠DAB.
综合应用
9.如图,在等腰三角形ABC中,AB=AC,以AC为直径作⊙O,与BC交于点E,过点E作ED⊥AB,垂足为D.求证:DE为⊙O的切线.
证明:连接OE,AE.
∵AC是⊙O的直径,∴∠AEC=90°.
又∵AB=AC, ∴∠B=∠C.
∵∠B=90°-∠DAE=∠DEA.
∴∠DEA=∠C,又∵OE=OA, ∴∠EAO=∠AEO
∴∠DEO=∠DEA+∠AEO=∠C+∠EAO=90°.
又DE过点E,∴DE为⊙O的切线.
10.如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4 cm,求阴影部分的面积.
拓展延伸
解:连接FO1、FO.过O作OM⊥AB于点M.
AB与⊙O相切,∴O1F⊥AB.
又∵AB∥CD,∴O1F⊥CD.
∴四边形FO1OM是矩形.
∴O1F=OM.
又∵OM⊥AB,∴MB= AB=2cm.
连接OB,在Rt△BMO中,OM2+MB2=OB2,
即O1F2+MB2=OB2.
∴S阴影= π·OB2- π·O1F2= π(OB2-O1F2)
= π·MB2= π×4=2π(cm2)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
章末复习
R·九年级上册
复习导入
本节课对全章的知识作一回顾,梳理其知识脉络,熟悉其知识构架,进一步澄清易混点,易错点,同时对本章中的一些常用辅助线和常见分类作一整理.
(1)梳理全章知识点,能画出它的知识结构框图.
(2)总结解题方法,提升解题能力.
知识结构
圆
圆的有关性质
圆的对称性
弧、弦、圆心角之间的关系
同弧上的圆周角和圆心角的关系
点、直线和圆
的位置关系
正多边形和圆
弧长和扇形面积
扇形面积
弧长
等分圆周
圆锥的侧面积和全面积
点和圆的位置关系
直线和圆的位置关系
切线
三角形的内切圆
三角形的外接圆
在本章,我们利用圆的对称性,探索了圆的一些重要性质;通过图形的运动,研究了点和圆、直线和圆、圆和圆的位置关系;同时研究了圆中的有关计算问题.
重点知识内容
1.
知识回顾
在同圆或等圆中, 相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距也相等.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
(1)在同圆或等圆中的弧、弦、圆心角有什么关系?
2.
·
O
A
B
A′
B′
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦(不是直径)所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
(4)圆的两条平行弦所夹的弧相等.
(2) 垂直于弦的直径有什么性质?
·
O
A
B
C
D
E
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
(3)一条弧所对的圆周角和它所对的圆心角有什么关系?
·
A
C1
O
C2
C3
B
·
A
C
B
O
点P在圆内 d < r .
点P在圆外 d > r ;
点P在圆上 d = r;
直线和⊙O相交
直线和⊙O相切
直线和⊙O相离
d<r;
d = r;
d>r.
(1)点和圆有怎样的位置关系?如何判定
(2)直线和圆的位置有几种,如何进行判定?
3.
r
·
O
A
P
P
P
·
l
O
r
l
l
d > r1+r2;
两圆外离
d = r1- r2;
两圆内切
d = r1+r2;
两圆外切
d< r1- r2.
两圆内含
r1-r2<d<r1+r2;
两圆相交
(3)圆和圆的位置关系有几种 如何判定
·
·
O2
O1
·
·
O1
O2
·
·
O1
O2
·
·
O1
O2
·
·
O2
O1
·
O
A
·
O
l
A
(1)圆的切线有什么性质?
圆的切线垂直于过切点的半径.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)如何判断一条直线是圆的切线?
4.
l
正多边形必有外接圆和内切圆.
(1)正多边形和圆有什么关系?
5.
(2) 你能用正多边形和等分圆周设计一些图案吗?
(1)举例说明如何计算弧长?
6.
·
O
n°
1°
1°的圆心角所对的弧长:
n°的圆心角所对的弧长:
(2)举例说明如何计算扇形面积.
1°圆心角的扇形面积:
n°圆心角的扇形的面积:
·
O
n°
则圆锥的侧面积为
圆锥的侧面展开图是一个扇形,设圆锥的母线长为l,底面圆的半径为r.
l
o
r
圆锥的全面积为
(3) 举例说明如何计算圆锥的侧面积和全面积.
随堂演练
基础巩固
1.如图,在⊙O中,弦AB,CD相交于点P,∠A=40°,∠APD=75°,则∠B等于( )
A.15° B.40° C.75° D.35°
D
2.如图,PA,PB分别切⊙O于点A,B,∠P=70°,则∠C=( )
A.70° B.55° C.110° D.140°
B
3.以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )
不能构成三角形
B. 这个三角形是等腰三角形
C. 这个三角形是直角三角形
D. 这个三角形是钝角三角形
C
4.一个圆锥的侧面积是底面积的 倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.180°
C.240° D.300°
C
5.如图所示,P是⊙O外一点,PA、PB分别和⊙O切于点A、B,点C是AB上任意一点,过点C作⊙O的切线分别交PA、PB于点D、E,若△PDE的周长为12,则PA的长为 .
6
⌒
6.如图,AC=CB,D,E分别是半径OA,OB的中点.求证:CD=CE.
证明:连接OC.
∵AC=CB,∴∠COD=∠COE.
∵D、E分别是半径OA、OB的中点,
∴OD=OE= OA= OB.
又OC=OC,
∴△COD≌△COE.∴CD=CE.
⌒
⌒
⌒
⌒
7.在直径为650mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB=600mm,求油的最大深度.
解:过O作OD⊥AB,交AB于点C,交⊙O于点D.
则AC= AB=300mm.
连接OA.设CD=xmm,则OC=(325-x)mm.
在Rt△AOC中,OC2+AC2=OA2,
即(325-x)2+3002=3252.解得x=200.
即CD=200mm.
答:油的最大深度为200mm.
8.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB.
证明:连接OC.
∵OA=OC,∴∠OAC=∠OCA.
又∵DC是⊙O的切线, ∴OC⊥CD.
又AD⊥CD,∴AD∥CO.
∴∠DAC=∠OCA,∴∠DAC=∠OAC.
∴AC平分∠DAB.
综合应用
9.如图,在等腰三角形ABC中,AB=AC,以AC为直径作⊙O,与BC交于点E,过点E作ED⊥AB,垂足为D.求证:DE为⊙O的切线.
证明:连接OE,AE.
∵AC是⊙O的直径,∴∠AEC=90°.
又∵AB=AC, ∴∠B=∠C.
∵∠B=90°-∠DAE=∠DEA.
∴∠DEA=∠C,又∵OE=OA, ∴∠EAO=∠AEO
∴∠DEO=∠DEA+∠AEO=∠C+∠EAO=90°.
又DE过点E,∴DE为⊙O的切线.
10.如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4 cm,求阴影部分的面积.
拓展延伸
解:连接FO1、FO.过O作OM⊥AB于点M.
AB与⊙O相切,∴O1F⊥AB.
又∵AB∥CD,∴O1F⊥CD.
∴四边形FO1OM是矩形.
∴O1F=OM.
又∵OM⊥AB,∴MB= AB=2cm.
连接OB,在Rt△BMO中,OM2+MB2=OB2,
即O1F2+MB2=OB2.
∴S阴影= π·OB2- π·O1F2= π(OB2-O1F2)
= π·MB2= π×4=2π(cm2)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
