【同步作业】人教版九(上) 21.3 实际问题与一元二次方程 第3课时 几何图形问题 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 21.3 实际问题与一元二次方程 第3课时 几何图形问题 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览







文档简介
(共23张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1如图,某地计划对长50m,
原广场
宽40m的矩形广场进行扩建改
充区域
造,要求扩建后的矩形广场长与
宽的比为3:2.扩充区域的扩建费用为每平方米30
元,扩建后在原广场和扩充区域都铺设地砖,铺设
地砖费用为每平方米100元.如果计划总费用为
642000元,那么扩建后广场的长和宽应分别是多少米?
分析:设扩建后广场的长为3xm,宽为2xm.
面积/m2
费用/元
总费用/元
原广场
50×40
3x·2x·100+
新广场
3x·2x
3x·2x·100
30(3x·2x-50×
40)
扩充区
3x·2x-50×40
30(3x·2x-50×40)
列方程
3x·2x·100+30(3x·2x-50×40)=642000
解:设扩建后广场的长为3xm,宽为2xm.
依题意,得3x·2x·100+30(3x·2x-50×40)=
642000.
解得x,=30,心2=-30(不合题意,舍去).
所以3x=90,2x=60
答:扩建后广场的长为90m,宽为60m.
1-1「古代数学文化]《杨辉算法》中记载:“直田积八百六十
四步,只云阔与长共六十步,问阔及长各几步.”意思是:一
块矩形田地的面积是864平方步,它的宽和长共60步,则
它的宽为24步,长为36步.
1-2[青海中考]如图,小明同学用一张长11cm,宽7cm的
矩形纸板制作一个底面积为21cm2的无盖长方体纸
盒,他将纸板的四个角各剪去一个同样大小的正方形,
将四周向上折叠即可(损耗不计).设剪去的正方形边长
为xcm,可列方程为(11-2x)(7-2x)=21.
1-3[泰州中考]如图,在长为50m,宽为38m的矩形地面
内的四周修筑同样宽的道路,余下的铺上草坪.要使草
坪的面积为1260m2,道路的宽应为
4
m.
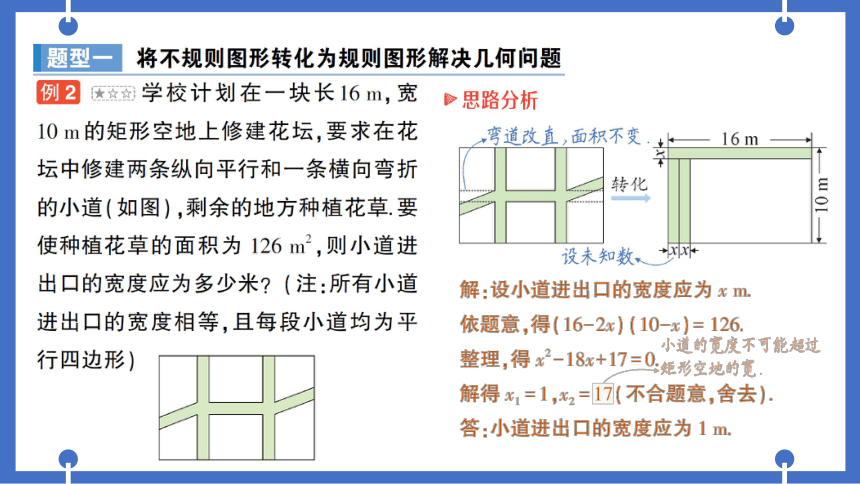
例2
女☆☆
学校计划在一块长16m,宽
10m的矩形空地上修建花坛,要求在花
坛中修建两条纵向平行和一条横向弯折
的小道(如图),剩余的地方种植花草.要
使种植花草的面积为126m,则小道进
出口的宽度应为多少米?(注:所有小道
进出口的宽度相等,且每段小道均为平
行四边形)
>思路分析
弯道改直,面积不变·
-16m±
转化
10m
↓
设未知数
解:设小道进出口的宽度应为xm
依题意,得(16-2x)(10-x)=126.
小道的宽度不可能超过
整理,得x2-18x+17=0矩形空地的宽
解得x1=1,x2=17(不合题意,舍去).
答:小道进出口的宽度应为1m
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1如图,某地计划对长50m,
原广场
宽40m的矩形广场进行扩建改
充区域
造,要求扩建后的矩形广场长与
宽的比为3:2.扩充区域的扩建费用为每平方米30
元,扩建后在原广场和扩充区域都铺设地砖,铺设
地砖费用为每平方米100元.如果计划总费用为
642000元,那么扩建后广场的长和宽应分别是多少米?
分析:设扩建后广场的长为3xm,宽为2xm.
面积/m2
费用/元
总费用/元
原广场
50×40
3x·2x·100+
新广场
3x·2x
3x·2x·100
30(3x·2x-50×
40)
扩充区
3x·2x-50×40
30(3x·2x-50×40)
列方程
3x·2x·100+30(3x·2x-50×40)=642000
解:设扩建后广场的长为3xm,宽为2xm.
依题意,得3x·2x·100+30(3x·2x-50×40)=
642000.
解得x,=30,心2=-30(不合题意,舍去).
所以3x=90,2x=60
答:扩建后广场的长为90m,宽为60m.
1-1「古代数学文化]《杨辉算法》中记载:“直田积八百六十
四步,只云阔与长共六十步,问阔及长各几步.”意思是:一
块矩形田地的面积是864平方步,它的宽和长共60步,则
它的宽为24步,长为36步.
1-2[青海中考]如图,小明同学用一张长11cm,宽7cm的
矩形纸板制作一个底面积为21cm2的无盖长方体纸
盒,他将纸板的四个角各剪去一个同样大小的正方形,
将四周向上折叠即可(损耗不计).设剪去的正方形边长
为xcm,可列方程为(11-2x)(7-2x)=21.
1-3[泰州中考]如图,在长为50m,宽为38m的矩形地面
内的四周修筑同样宽的道路,余下的铺上草坪.要使草
坪的面积为1260m2,道路的宽应为
4
m.
例2
女☆☆
学校计划在一块长16m,宽
10m的矩形空地上修建花坛,要求在花
坛中修建两条纵向平行和一条横向弯折
的小道(如图),剩余的地方种植花草.要
使种植花草的面积为126m,则小道进
出口的宽度应为多少米?(注:所有小道
进出口的宽度相等,且每段小道均为平
行四边形)
>思路分析
弯道改直,面积不变·
-16m±
转化
10m
↓
设未知数
解:设小道进出口的宽度应为xm
依题意,得(16-2x)(10-x)=126.
小道的宽度不可能超过
整理,得x2-18x+17=0矩形空地的宽
解得x1=1,x2=17(不合题意,舍去).
答:小道进出口的宽度应为1m
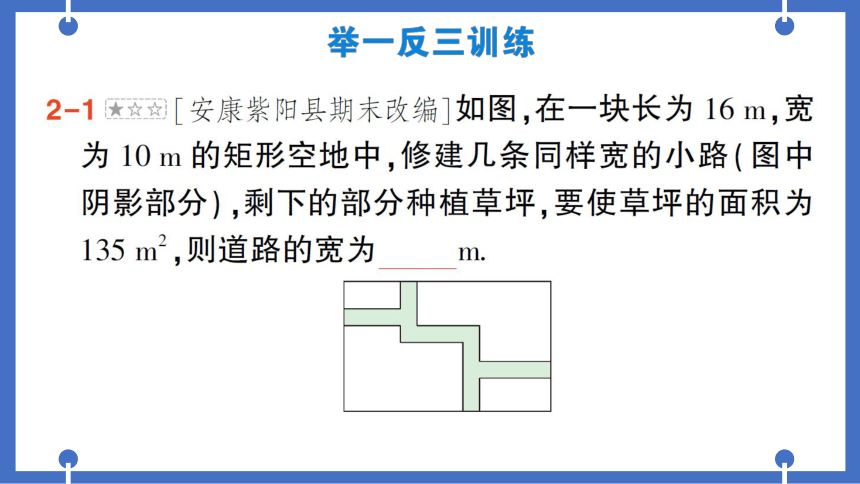
同课章节目录
