【同步作业】人教版九(上) 22.1 二次函数的图象和性质 22.1.1 二次函数 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 22.1 二次函数的图象和性质 22.1.1 二次函数 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览








文档简介
(共28张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
22.1
二次函数的图象和性质
22.1.1
二次函数
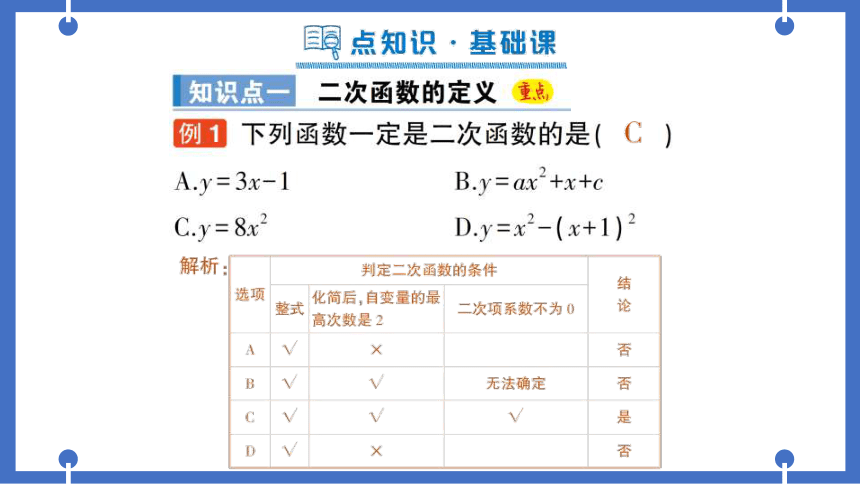
例1下列函数一定是二次函数的是(
)
A.y=3x-1
B.y=ax-+x+c
C.y=8x2
D.y=x2-(x+1)2
解析:
判定二次函数的条件
结
选项
化简后,自变量的最
整式
二次项系数不为0
论
高次数是2
A
X
否
B
W
无法确定
否
C
W
是
D
×
否
腕解题策略判断一个函数是否为二次函数的“三步骤”:
形式→
看函数解析式是否为整式
化简→将函数解析式化简
判断→看系数、次数是否符合要求
1-1下列各式中,一定是二次函数的有(B)
X
②y2=2x2+3;
③y=(2x-3)(3x-2);
④y=2x2-(2x2+5x);
⑤y=mx2+nx+p;
⑥y=(n2+1)x2-2x-3.
1-2若关于x的函数y=(2-a)x2-x是二次函数,则a的
取值范围是(B)
A.a≠0
B.a≠2
C.u<2
D.u>2
1-3已知关于x的函数y=xm-是二次函数,则m=3
1-4「对比学习]已知y关于x的函数解析式为y=(a-
25)x2+(a-5)x+3.
(1)当a取何值时,y与x之间是二次函数关系?
解:由题意,得w-25≠0,
则a≠±5.
所以当a≠±5时,y与x之间是二次函数关系.
解:因为y=2x2-(x+1)2=2x2-(x2+2x+1)=x2-2x-1,
即y=x2-2x-1,所以其二次项系数为1,一次项系数为-
2,常数项为-1.
肠知识点晴(1)确定二次函数的二次项系数、一次项系数和常数
项时,要先将解析式化成y=x2+bx+c(u≠0)的形式;(2)二次函
数解析式的二次项系数、一次项系数和常数项包括它们前面的符
号
注意不要漏掉
例3
九年级共有x名同学,在开学见面时每两名同学
都握手一次,共握手y次.试写出y与x之间的函数关系
式,并判断y是不是x的二次函数
>思路分析
共有x名同学
每人需要和(x-1)人握手一次
判断函数类型
列关系式
3-1共享单车被称为“中国新四大发明”之一.某单车公
司第一个月投放辆单车,计划第三个月投放y辆单
车,设该公司第二、三两个月投放单车数量的月平均
增长率为x,那么y与x的函数关系式是(B)
A.y=x2+a
B.y=a(1+x)
C.y=(1-x)2+a
D.y=a(1-x)2
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
22.1
二次函数的图象和性质
22.1.1
二次函数
例1下列函数一定是二次函数的是(
)
A.y=3x-1
B.y=ax-+x+c
C.y=8x2
D.y=x2-(x+1)2
解析:
判定二次函数的条件
结
选项
化简后,自变量的最
整式
二次项系数不为0
论
高次数是2
A
X
否
B
W
无法确定
否
C
W
是
D
×
否
腕解题策略判断一个函数是否为二次函数的“三步骤”:
形式→
看函数解析式是否为整式
化简→将函数解析式化简
判断→看系数、次数是否符合要求
1-1下列各式中,一定是二次函数的有(B)
X
②y2=2x2+3;
③y=(2x-3)(3x-2);
④y=2x2-(2x2+5x);
⑤y=mx2+nx+p;
⑥y=(n2+1)x2-2x-3.
1-2若关于x的函数y=(2-a)x2-x是二次函数,则a的
取值范围是(B)
A.a≠0
B.a≠2
C.u<2
D.u>2
1-3已知关于x的函数y=xm-是二次函数,则m=3
1-4「对比学习]已知y关于x的函数解析式为y=(a-
25)x2+(a-5)x+3.
(1)当a取何值时,y与x之间是二次函数关系?
解:由题意,得w-25≠0,
则a≠±5.
所以当a≠±5时,y与x之间是二次函数关系.
解:因为y=2x2-(x+1)2=2x2-(x2+2x+1)=x2-2x-1,
即y=x2-2x-1,所以其二次项系数为1,一次项系数为-
2,常数项为-1.
肠知识点晴(1)确定二次函数的二次项系数、一次项系数和常数
项时,要先将解析式化成y=x2+bx+c(u≠0)的形式;(2)二次函
数解析式的二次项系数、一次项系数和常数项包括它们前面的符
号
注意不要漏掉
例3
九年级共有x名同学,在开学见面时每两名同学
都握手一次,共握手y次.试写出y与x之间的函数关系
式,并判断y是不是x的二次函数
>思路分析
共有x名同学
每人需要和(x-1)人握手一次
判断函数类型
列关系式
3-1共享单车被称为“中国新四大发明”之一.某单车公
司第一个月投放辆单车,计划第三个月投放y辆单
车,设该公司第二、三两个月投放单车数量的月平均
增长率为x,那么y与x的函数关系式是(B)
A.y=x2+a
B.y=a(1+x)
C.y=(1-x)2+a
D.y=a(1-x)2
同课章节目录
