【同步作业】人教版九(上) 22.3 实际问题与二次函数 第3课时 二次函数与抛物线形的实际问题 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 22.3 实际问题与二次函数 第3课时 二次函数与抛物线形的实际问题 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览








文档简介
(共30张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1「衢州中考1某游乐园有一个直径为16m的圆形喷
水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物
线形,在距水池中心3m处达到最高,高度为5m,且各
方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如
图,以水平方向为x轴,喷水池中心为原点建立平面直
角坐标系
(1)求水柱所在抛物线(第一象限部分)的解析式,
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,
为了不被淋湿,身高1.8m的王师傅站立时必须在离水
池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改
进:在喷出水柱的形状不变的前提下,把水池的直径扩
大到32,各方向喷出的水柱仍在喷水池中心保留的原
装饰物(高度不变)处汇合,请探究扩建改造后喷水池水
柱的最大高度.
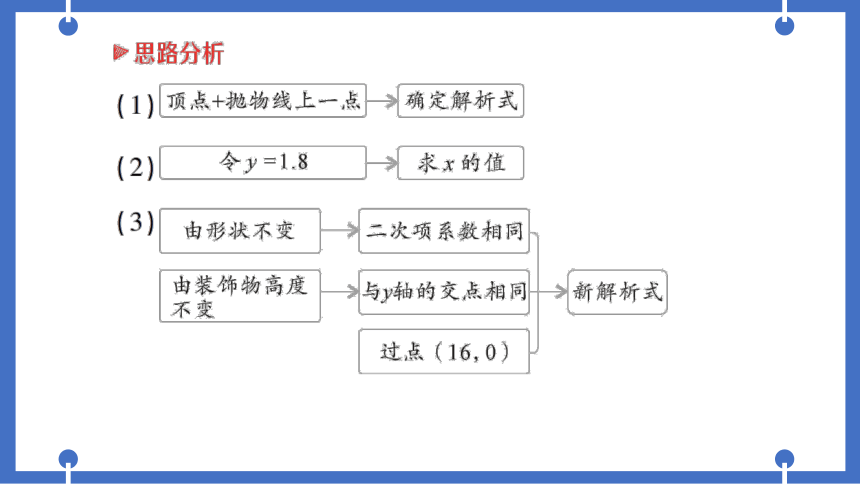
②思路分析
(1)
顶点十抛物线上一点
确定解析式
(2)
令y=1.8
求x的值
(3)
由形状不变
二次项系数相同
由装饰物高度
>
与y轴的交点相同>新解析式
不变
过点(16,0)
解:(1)设水柱所在抛物线(第一象限部分)的解析式为
y=a(x-3)2+5(≠0).将(8,0)代入y=a(x-3)2+5,得
25a+5=0.解得a=-5.所以水柱所在抛物线(第一象限
部分)的解析式为y=-5(x-3)+5(0<<8).
(2)当y=1.8时,有-5(x-3)2+5=1.8.解得x,=-1(不
16
合题意,舍去),=7.当x=0时,=5×(0-3)°+5=
5
>1.8.所以为了不被淋湿,身高1.8m的王师傅站立时必
须在离水池中心7m以内.
(3)设改造后水柱所在抛物线(第一象限部分)的解析
式为=+bx+
16
因为该抛物线过点(16,0),所以0
5
6
二
5
16+160+15解得=3所以y=-+3x+
5
5
15
289
l x
+20
所以扩建改造后喷水池水柱的最大高
289
度为
m.
1-1[上海杨浦区期末]广场上喷水池中的喷头微露水面,
喷出的水线是一条抛物线,水线上水珠的竖直高度
y(单位:m)关于水珠与喷头的水平距离x(单位:m)的
3
函数解析武为=,+6m0≤x≤4,那么水珠的
直高度达到最大时,水珠与喷头的水平距离是(B)
A.1 m
B.2 m
C.5 m
D.6 m
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1「衢州中考1某游乐园有一个直径为16m的圆形喷
水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物
线形,在距水池中心3m处达到最高,高度为5m,且各
方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如
图,以水平方向为x轴,喷水池中心为原点建立平面直
角坐标系
(1)求水柱所在抛物线(第一象限部分)的解析式,
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,
为了不被淋湿,身高1.8m的王师傅站立时必须在离水
池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改
进:在喷出水柱的形状不变的前提下,把水池的直径扩
大到32,各方向喷出的水柱仍在喷水池中心保留的原
装饰物(高度不变)处汇合,请探究扩建改造后喷水池水
柱的最大高度.
②思路分析
(1)
顶点十抛物线上一点
确定解析式
(2)
令y=1.8
求x的值
(3)
由形状不变
二次项系数相同
由装饰物高度
>
与y轴的交点相同>新解析式
不变
过点(16,0)
解:(1)设水柱所在抛物线(第一象限部分)的解析式为
y=a(x-3)2+5(≠0).将(8,0)代入y=a(x-3)2+5,得
25a+5=0.解得a=-5.所以水柱所在抛物线(第一象限
部分)的解析式为y=-5(x-3)+5(0<<8).
(2)当y=1.8时,有-5(x-3)2+5=1.8.解得x,=-1(不
16
合题意,舍去),=7.当x=0时,=5×(0-3)°+5=
5
>1.8.所以为了不被淋湿,身高1.8m的王师傅站立时必
须在离水池中心7m以内.
(3)设改造后水柱所在抛物线(第一象限部分)的解析
式为=+bx+
16
因为该抛物线过点(16,0),所以0
5
6
二
5
16+160+15解得=3所以y=-+3x+
5
5
15
289
l x
+20
所以扩建改造后喷水池水柱的最大高
289
度为
m.
1-1[上海杨浦区期末]广场上喷水池中的喷头微露水面,
喷出的水线是一条抛物线,水线上水珠的竖直高度
y(单位:m)关于水珠与喷头的水平距离x(单位:m)的
3
函数解析武为=,+6m0≤x≤4,那么水珠的
直高度达到最大时,水珠与喷头的水平距离是(B)
A.1 m
B.2 m
C.5 m
D.6 m
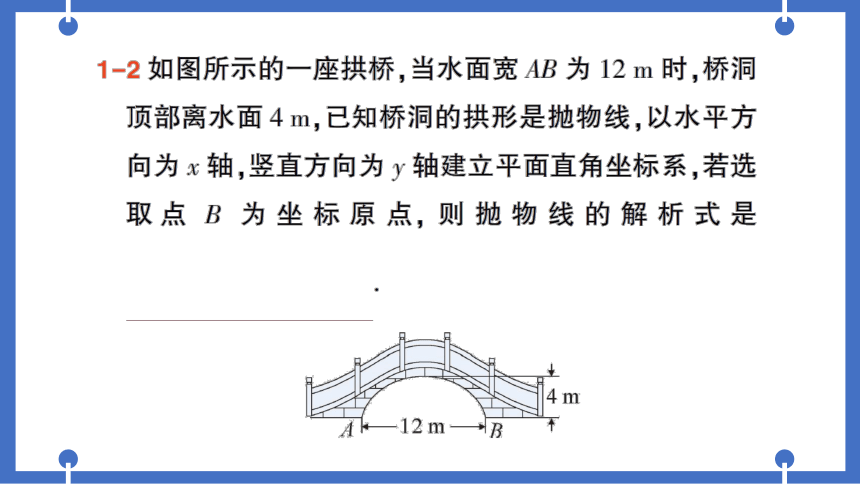
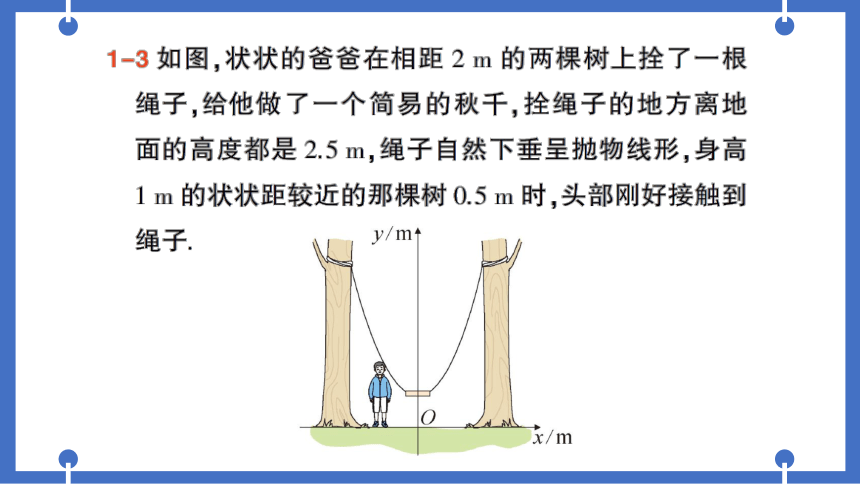
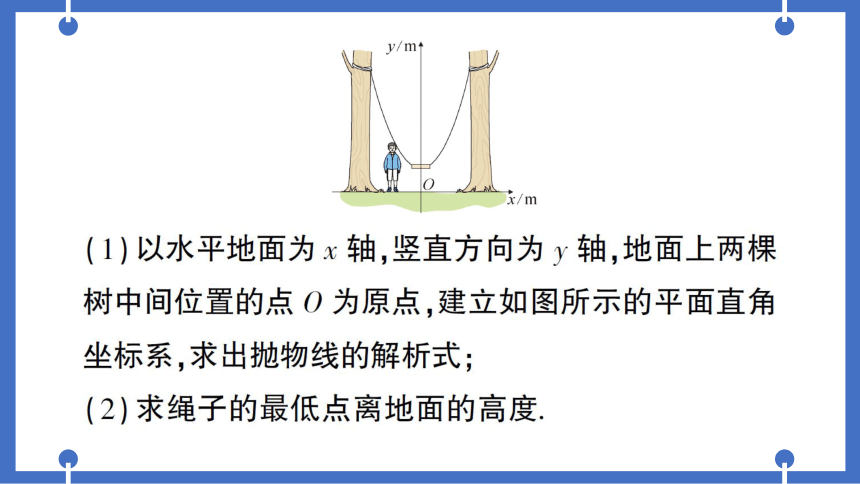
同课章节目录
