【同步作业】人教版九(上) 22.1 二次函数的图象和性质 22.1.4 二次函数y=ax2+bx+c的图象和性质 第2课时 用待定系数法求二次函数的解析式 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 22.1 二次函数的图象和性质 22.1.4 二次函数y=ax2+bx+c的图象和性质 第2课时 用待定系数法求二次函数的解析式 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览











文档简介
(共37张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1(1)己知抛物线的顶点为(1,-3),且经过点(-2,
设顶点式
0),则该抛物线的解析式为
(2)己知抛物线经过点(-1,0),(1,8)和(3,0),则该抛
物线的解析式为
设交点式
(3)己知抛物线经过(-1,10),(0,6),(1,4)三点,则该
抛物线的解析式为
解析:(1)设抛物线的解析式为y=a(x-1)2-3,把(-2,
0)代入,得9α-3=0,解得u=。.所以该抛物线的解析式
3
2
为
Y=
。(x-1)2-3,即y=
+另解:也可设一般式求解
(2)设抛物线的解析式为y=a(x+1)(x-3),把(1,8)代
入,得-4a=8,解得a=-2.所以该抛物线的解析式为y=
-2(x+1)(x-3),即y=-2x2+4x+6.
(3)设抛物线的解析式为y=ax2+bx+c,把(-1,10),(0,
a-b+c=10,
a=1,
6),(1,4)分别代入,得c=6,
解得b=-3,所以该抛
a+b+c=4,
c=6.
物线的解析式为y=x2-3x+6.
1-3[江油期末]己知二次函数的图象经过(-1,0),(3,
0),(0,3)三点,那么这个二次函数的解析式为
y=-x2+2x+3
1-4已知一条抛物线的形状、开口方向与y=。x2-4+3
2
相同,且经过(-1,0),(0,5)两点,则此抛物线的解析式
11
为
y=
+x+5
2
●
1-5「
新定义]设抛物线G:y=x2+bx+c的顶点为D,与y
轴交于点C,我们称以C为顶点,且过点D的抛物线
为抛物线G的“伴随抛物线”,请写出抛物线y=x2-4x
+1的“伴随抛物线”的解析式:y=-x2+1
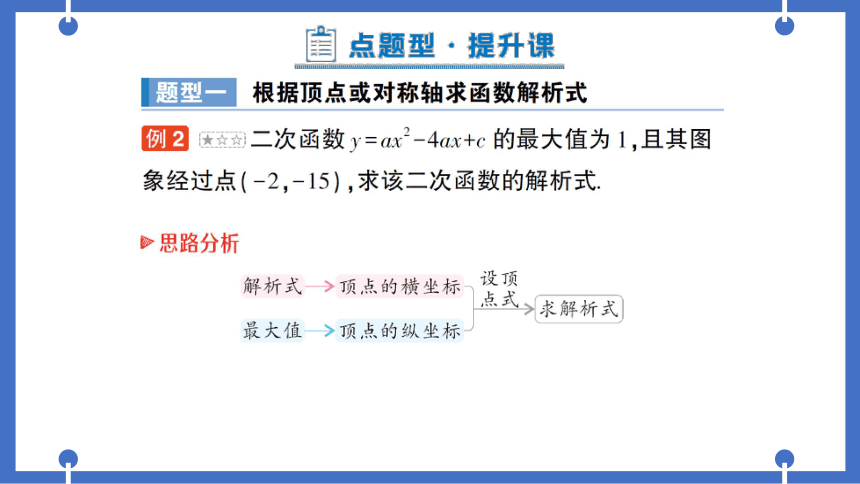
题型
根据顶点或对称轴求函数解析式
例2
女☆☆
二次函数y=ax2-4ax+c的最大值为1,且其图
象经过点(-2,-15),求该二次函数的解析式
畛思路分析
解析式>顶点的横坐标
设顶
点式
求解析式
最大值>顶,点的纵坐标
-40
解:由题意,得抛物线的对称轴为直线x=
=2.因为
20
二次函数的最大值为1,所以抛物线的顶点坐标为(2,
1).所以该二次函数的解析式可化为y=a(x-2)2+1.将
(-2,-15)代入,得-15=u×(-2-2)2+1,解得a=-1.
所以该二次函数的解析式为y=-(x-2)2+1,即y=-x2+
4x-3.
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1(1)己知抛物线的顶点为(1,-3),且经过点(-2,
设顶点式
0),则该抛物线的解析式为
(2)己知抛物线经过点(-1,0),(1,8)和(3,0),则该抛
物线的解析式为
设交点式
(3)己知抛物线经过(-1,10),(0,6),(1,4)三点,则该
抛物线的解析式为
解析:(1)设抛物线的解析式为y=a(x-1)2-3,把(-2,
0)代入,得9α-3=0,解得u=。.所以该抛物线的解析式
3
2
为
Y=
。(x-1)2-3,即y=
+另解:也可设一般式求解
(2)设抛物线的解析式为y=a(x+1)(x-3),把(1,8)代
入,得-4a=8,解得a=-2.所以该抛物线的解析式为y=
-2(x+1)(x-3),即y=-2x2+4x+6.
(3)设抛物线的解析式为y=ax2+bx+c,把(-1,10),(0,
a-b+c=10,
a=1,
6),(1,4)分别代入,得c=6,
解得b=-3,所以该抛
a+b+c=4,
c=6.
物线的解析式为y=x2-3x+6.
1-3[江油期末]己知二次函数的图象经过(-1,0),(3,
0),(0,3)三点,那么这个二次函数的解析式为
y=-x2+2x+3
1-4已知一条抛物线的形状、开口方向与y=。x2-4+3
2
相同,且经过(-1,0),(0,5)两点,则此抛物线的解析式
11
为
y=
+x+5
2
●
1-5「
新定义]设抛物线G:y=x2+bx+c的顶点为D,与y
轴交于点C,我们称以C为顶点,且过点D的抛物线
为抛物线G的“伴随抛物线”,请写出抛物线y=x2-4x
+1的“伴随抛物线”的解析式:y=-x2+1
题型
根据顶点或对称轴求函数解析式
例2
女☆☆
二次函数y=ax2-4ax+c的最大值为1,且其图
象经过点(-2,-15),求该二次函数的解析式
畛思路分析
解析式>顶点的横坐标
设顶
点式
求解析式
最大值>顶,点的纵坐标
-40
解:由题意,得抛物线的对称轴为直线x=
=2.因为
20
二次函数的最大值为1,所以抛物线的顶点坐标为(2,
1).所以该二次函数的解析式可化为y=a(x-2)2+1.将
(-2,-15)代入,得-15=u×(-2-2)2+1,解得a=-1.
所以该二次函数的解析式为y=-(x-2)2+1,即y=-x2+
4x-3.
同课章节目录
