【同步作业】人教版九(上) 22.3 实际问题与二次函数 第1课时 二次函数与图形面积问题 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 22.3 实际问题与二次函数 第1课时 二次函数与图形面积问题 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览







文档简介
(共23张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
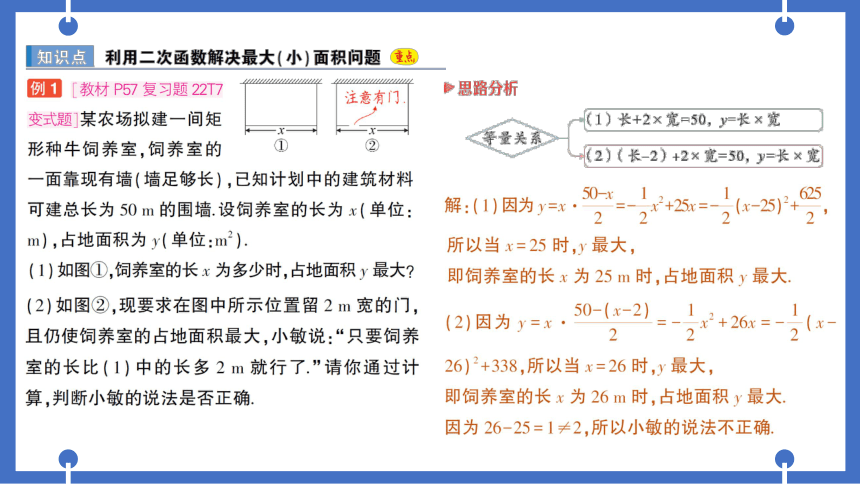
例1「教材P57复习题22T7
注意有门
变式题某农场拟建一间矩
形种牛饲养室,饲养室的
一面靠现有墙(墙足够长),已知计划中的建筑材料
可建总长为50m的围墙.设饲养室的长为x(单位:
m),占地面积为y(单位:m2).
(1)如图①,饲养室的长x为多少时,占地面积y最大?
(2)如图②,现要求在图中所示位置留2宽的门
且仍使饲养室的占地面积最大,小敏说:“只要饲养
室的长比(1)中的长多2m就行了.”请你通过计
算,判断小敏的说法是否正确
>思路分析
(1)长+2×宽=50,y=长×宽
等量关系
(2)(长-2)+2×宽=50,y=长×宽
(2)因为y=x·
50-(x-2)--
2
2
2+26x=-
26)2+338,所以当x=26时,y最大,
即饲养室的长x为26m时,占地面积y最大,
因为26-25=1≠2,所以小敏的说法不正确.
1-1某高中为高一新生设计了一款单人桌,桌子抽屉的形
状是长方体,其底面周长为180cm,高为20cm.则当底
面的宽x为45cm时,抽屉的容积y最大.(材质及
其厚度等忽略不计)
1-2「教材P56复习题22T1变式题7如图,四边形ABCD是一
块边长为8的正方形苗圃,园林部门拟将其改造为
矩形苗圃AEFG,其中点E在AB边上,点G在AD的延
长线上,DG=2BE,设BE的长为x,改造后苗圃的面
积为ym2.
A
D
G
E
H
F
B
C
(2)当x为何值时,改造后的矩形苗圃AEFG的面积最
大?并求出最大面积.
解:因为y=-2x2+8x+64=-2(x-2)2+72,
所以当x=2时,y有最大值72,则当x为2时,改造后的矩形苗圃AEFG
的面积最大,最大面积为72m2.
A
D
G
E
H
F
B
C
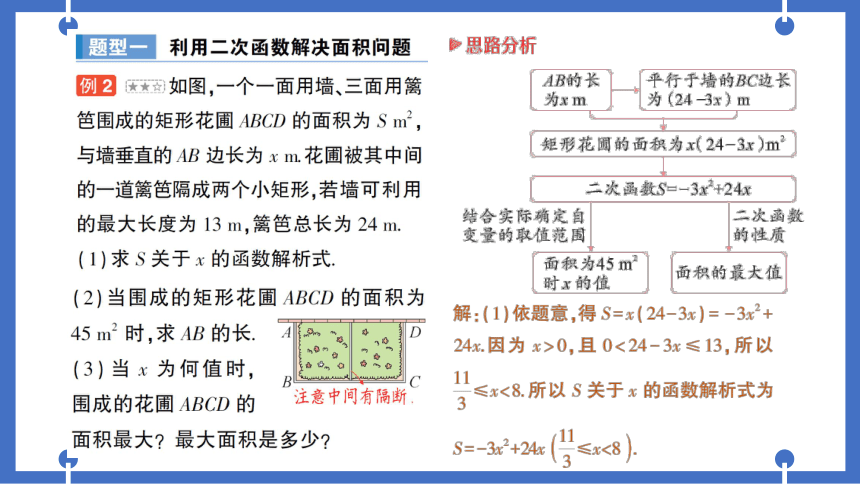
题型
利用二次函数解决面积问题
例2
女女对
如图,一个一面用墙、三面用篱
笆围成的矩形花圃ABCD的面积为Sm
与墙垂直的AB边长为xm.花圃被其中间
的一道篱笆隔成两个小矩形,若墙可利用
的最大长度为13m,篱笆总长为24m,
(1)求S关于x的函数解析式
(2)当围成的矩形花圃ABCD的面积为
45m2时,求AB的长.
(3)当x为何值时,
3
计
人人
围成的花圃ABCD的
注意中间有隔断
面积最大?最大面积是多少?
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1「教材P57复习题22T7
注意有门
变式题某农场拟建一间矩
形种牛饲养室,饲养室的
一面靠现有墙(墙足够长),已知计划中的建筑材料
可建总长为50m的围墙.设饲养室的长为x(单位:
m),占地面积为y(单位:m2).
(1)如图①,饲养室的长x为多少时,占地面积y最大?
(2)如图②,现要求在图中所示位置留2宽的门
且仍使饲养室的占地面积最大,小敏说:“只要饲养
室的长比(1)中的长多2m就行了.”请你通过计
算,判断小敏的说法是否正确
>思路分析
(1)长+2×宽=50,y=长×宽
等量关系
(2)(长-2)+2×宽=50,y=长×宽
(2)因为y=x·
50-(x-2)--
2
2
2+26x=-
26)2+338,所以当x=26时,y最大,
即饲养室的长x为26m时,占地面积y最大,
因为26-25=1≠2,所以小敏的说法不正确.
1-1某高中为高一新生设计了一款单人桌,桌子抽屉的形
状是长方体,其底面周长为180cm,高为20cm.则当底
面的宽x为45cm时,抽屉的容积y最大.(材质及
其厚度等忽略不计)
1-2「教材P56复习题22T1变式题7如图,四边形ABCD是一
块边长为8的正方形苗圃,园林部门拟将其改造为
矩形苗圃AEFG,其中点E在AB边上,点G在AD的延
长线上,DG=2BE,设BE的长为x,改造后苗圃的面
积为ym2.
A
D
G
E
H
F
B
C
(2)当x为何值时,改造后的矩形苗圃AEFG的面积最
大?并求出最大面积.
解:因为y=-2x2+8x+64=-2(x-2)2+72,
所以当x=2时,y有最大值72,则当x为2时,改造后的矩形苗圃AEFG
的面积最大,最大面积为72m2.
A
D
G
E
H
F
B
C
题型
利用二次函数解决面积问题
例2
女女对
如图,一个一面用墙、三面用篱
笆围成的矩形花圃ABCD的面积为Sm
与墙垂直的AB边长为xm.花圃被其中间
的一道篱笆隔成两个小矩形,若墙可利用
的最大长度为13m,篱笆总长为24m,
(1)求S关于x的函数解析式
(2)当围成的矩形花圃ABCD的面积为
45m2时,求AB的长.
(3)当x为何值时,
3
计
人人
围成的花圃ABCD的
注意中间有隔断
面积最大?最大面积是多少?
同课章节目录
