【同步作业】人教版九(上) 22.3 实际问题与二次函数 第2课时 二次函数与最大利润问题 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 22.3 实际问题与二次函数 第2课时 二次函数与最大利润问题 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览








文档简介
(共27张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1:
某企业设计了一款工艺品,每件的成本是50元
为了合理定价,投放市场进行试销.据市场调查,销售单
价是100元时,每天的销售量是50件,而销售单价每降
低1元,每天就可多售出5件,但要求销售单价不得低
于成本,且不高于100元.
(1)求每天的销售利润y(单位:元)与销售单价x(单位:
元)之间的函数关系式:
(2)销售单价为多少元时,每天的销售利润最大?最大
利润是多少?
分析:
成本/
销售单
销售量/件
销售利润/元
(元/件)
价/元
降价前
50
100
50
(100-50)×50=2500
降价后
50
X
50+5(100-x)
(x-50)[50+5(100-x)]
(2)y=-5x2+800x-27500=-5(x-80)2+4500
因为-5<0,50≤x≤100,所以当x=80时,y有最大值4
500,即销售单价为80元时,每天的销售利润最大,最大
利润是4500元.
2知识点睛(1)对于“每…每.”类型的二次函数型实际问
题,在没有要求的情况下,如果自变量设“降价幅度”或“涨价幅
度”,那么计算的数据较小;如果自变量设“销售单价”,那么计算
的数据较大.(2)若每涨n元,就少卖m件,则每涨1元,就少卖
件;若每降4元,就多卖b件,则每降1元,就多卖6件.(3)若对称
轴在自变量的取值范围内,则当抛物线开口向上时,在顶点处函数
取得最小值,自变量取值离对称轴越远函数值越大,离对称轴越近
函数值越小;当抛物线开口向下时,在顶点处函数取得最大值,自
变量取值离对称轴越近函数值越大,离对称轴越远函数值越小,
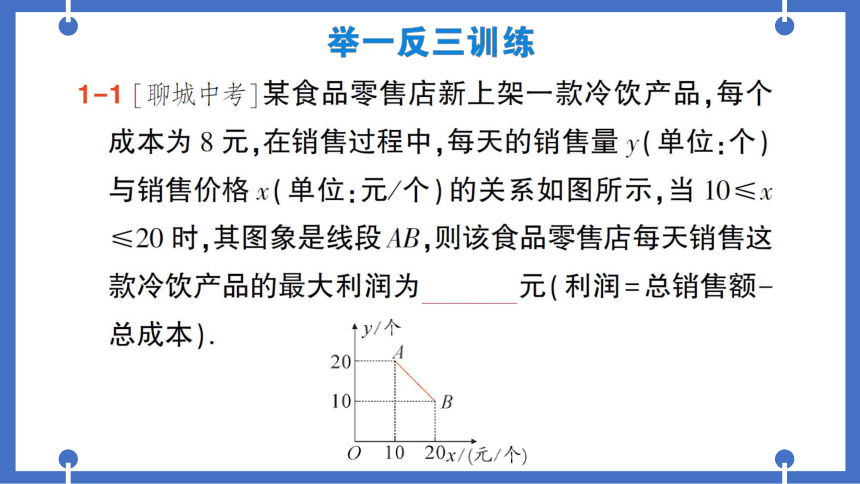
1-1「聊城中考]某食品零售店新上架一款冷饮产品,每个
成本为8元,在销售过程中,每天的销售量y(单位:个)
与销售价格x(单位:元/个)的关系如图所示,当10≤x
≤20时,其图象是线段AB,则该食品零售店每天销售这
款冷饮产品的最大利润为
121元(利润=总销售额-
总成本)
↑y/个
20
10
B
0
10
20x/(元/个)
1-2某商场销售一款小商品,进货价为40元/件.当销售
单价为60元时,每天的销售量为300件.在销售过程
中发现:销售单价每上张2元,每天的销售量就减少20
件.设销售单价上涨x元(x为偶数),每天的销售量为
y件
(1)求y与x之间的函数关系式
解:根据题意可知y=00-〉·20=300-10x
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1:
某企业设计了一款工艺品,每件的成本是50元
为了合理定价,投放市场进行试销.据市场调查,销售单
价是100元时,每天的销售量是50件,而销售单价每降
低1元,每天就可多售出5件,但要求销售单价不得低
于成本,且不高于100元.
(1)求每天的销售利润y(单位:元)与销售单价x(单位:
元)之间的函数关系式:
(2)销售单价为多少元时,每天的销售利润最大?最大
利润是多少?
分析:
成本/
销售单
销售量/件
销售利润/元
(元/件)
价/元
降价前
50
100
50
(100-50)×50=2500
降价后
50
X
50+5(100-x)
(x-50)[50+5(100-x)]
(2)y=-5x2+800x-27500=-5(x-80)2+4500
因为-5<0,50≤x≤100,所以当x=80时,y有最大值4
500,即销售单价为80元时,每天的销售利润最大,最大
利润是4500元.
2知识点睛(1)对于“每…每.”类型的二次函数型实际问
题,在没有要求的情况下,如果自变量设“降价幅度”或“涨价幅
度”,那么计算的数据较小;如果自变量设“销售单价”,那么计算
的数据较大.(2)若每涨n元,就少卖m件,则每涨1元,就少卖
件;若每降4元,就多卖b件,则每降1元,就多卖6件.(3)若对称
轴在自变量的取值范围内,则当抛物线开口向上时,在顶点处函数
取得最小值,自变量取值离对称轴越远函数值越大,离对称轴越近
函数值越小;当抛物线开口向下时,在顶点处函数取得最大值,自
变量取值离对称轴越近函数值越大,离对称轴越远函数值越小,
1-1「聊城中考]某食品零售店新上架一款冷饮产品,每个
成本为8元,在销售过程中,每天的销售量y(单位:个)
与销售价格x(单位:元/个)的关系如图所示,当10≤x
≤20时,其图象是线段AB,则该食品零售店每天销售这
款冷饮产品的最大利润为
121元(利润=总销售额-
总成本)
↑y/个
20
10
B
0
10
20x/(元/个)
1-2某商场销售一款小商品,进货价为40元/件.当销售
单价为60元时,每天的销售量为300件.在销售过程
中发现:销售单价每上张2元,每天的销售量就减少20
件.设销售单价上涨x元(x为偶数),每天的销售量为
y件
(1)求y与x之间的函数关系式
解:根据题意可知y=00-〉·20=300-10x
同课章节目录
