【同步作业】人教版九(上) 24.1 圆的有关性质 24.1.4 圆周角 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 24.1 圆的有关性质 24.1.4 圆周角 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 00:00:00 | ||
图片预览




文档简介
(共41张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
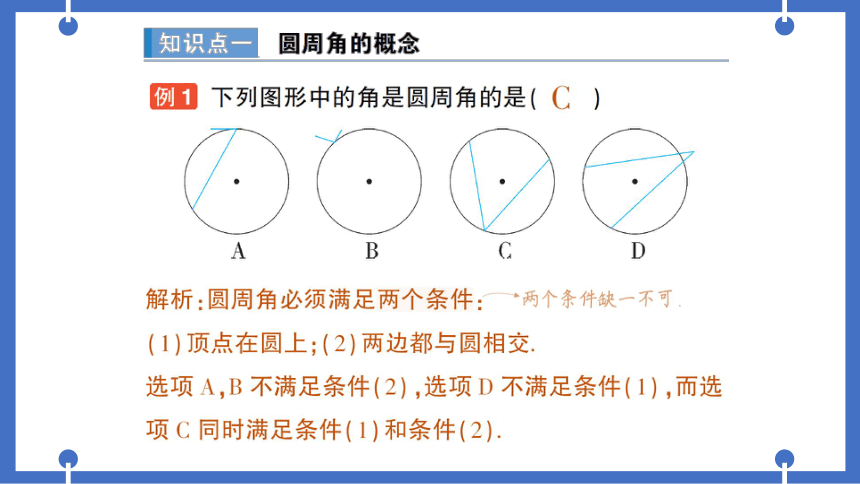
例1下列图形中的角是圆周角的是(
A
B
C
D
解析:圆周角必须满足两个条件:·两个条件缺一不可.
(1)顶点在圆上;(2)两边都与圆相交
选项A,B不满足条件(2),选项D不满足条件(1),而选
项C同时满足条件(1)和条件(2).
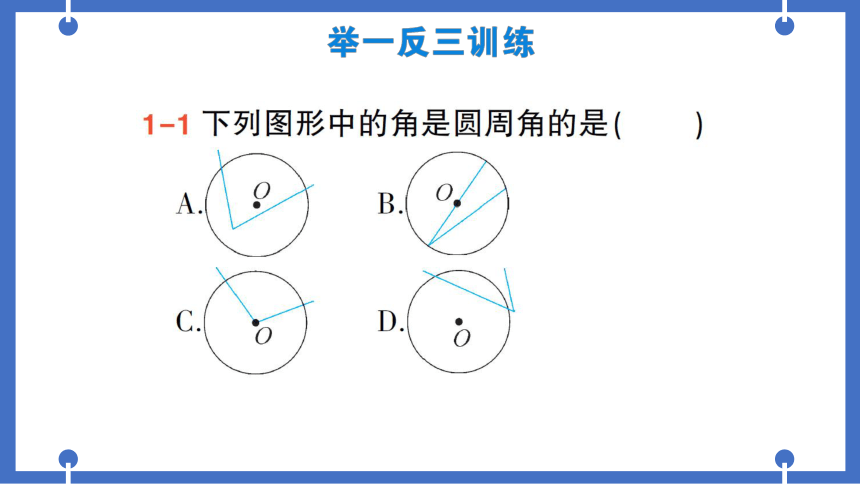
1-1下列图形中的角是圆周角的是(B)
B
D
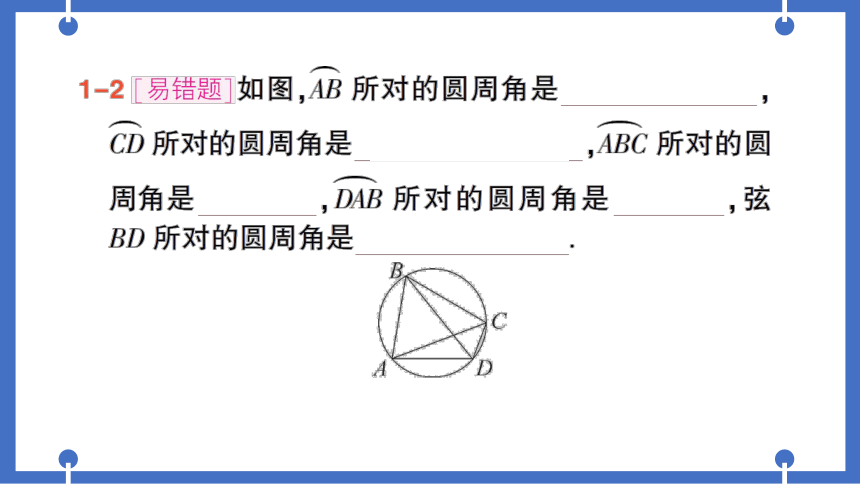
1-2[易错题]如图,AB所对的圆周角是∠ADB,∠ACB
CD所对的圆周角是
∠DAC,∠DBC,ABC所对的圆
周角是∠ADC,DAB所对的圆周角是∠BCD,弦
BD所对的圆周角是∠BCD,∠BAD
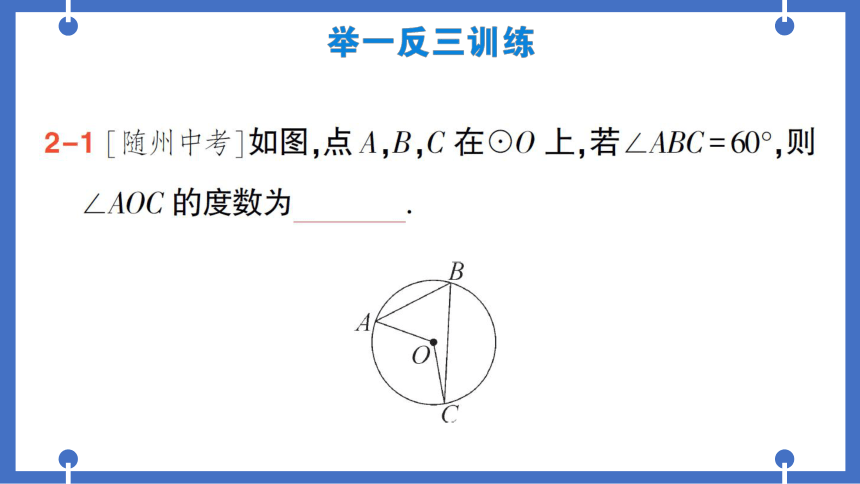
例2[内江中考]如图,点A,B,C,D在⊙O
B
上,∠AOC=120°,B是AC的中点,则∠D
的度数是(
A.30°
B.40°
C.50°
D.60°
>思路分析
已知条件
孤、弦、圆心
角之间的关系
圆周角定理
∠AOC=120°,
∠AOB=∠BOC=60→,
B是AC的中点
D=
40B-30
0
B
C
@思路分析
圆周角
直角三
圆周角
定理的
角形的
定理的
推论2
性质
推论1
∠ACB=90°
求∠BAC
∠BDC=∠BAC
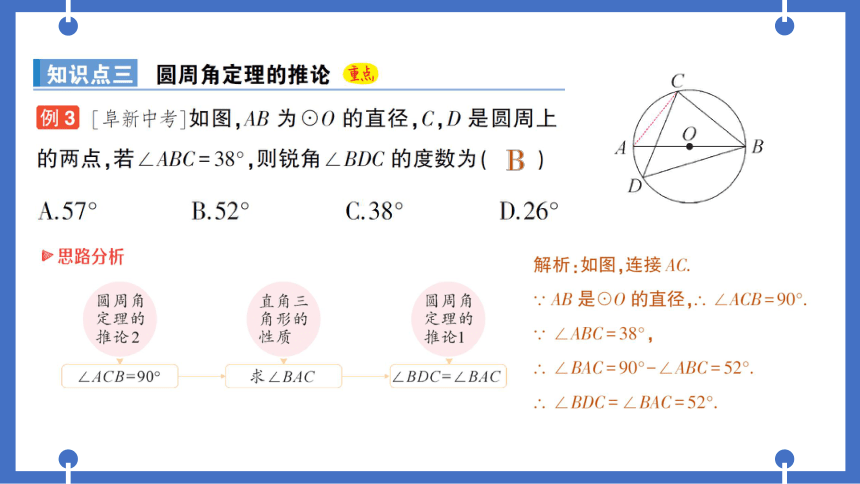
解析:如图,连接AC
.AB是⊙O的直径,∴.∠ACB=90°.
.·∠ABC=38°,
.∠BAC=90°-∠ABC=52°.
∴.∠BDC=∠BAC=52°.
方法总结运用圆周角定理的推论2作辅助线的方法:
(1)有直径,通常作直径所对的圆周角,从而得到90°的角.简记
为:见直径作直角
(2)有90°的圆周角,通常作直径.简记为:有直角作直径
3-1用直角三角尺检查半圆形的工件,下列工件中合格
的是(C)
B.
3-2[柳州中考]如图,A,B,C,D是⊙0上的点,则图中与
∠A相等的角是(D)
A.∠B
B
A
B.∠C
E
0
C.∠DEB
D.∠D
3-4[黔东南州中考改编]如图,在Rt△ACB中,∠ACB=90°,
AC=6,BC=8,若以AC为直径的⊙O交AB于点D,则
CD的长为
4.8
A
D
0
C
B
D
A
B
C
>思路分析
四边形ABCD内接于⊙O
∠A+∠C=180°
∠A=105°
∠C=75
∠BOD=2∠C=150°
4-1[重庆中考A卷]如图,四边形ABCD内接于⊙O,若
∠A=80°,则C的度数是(B)
A.80°
B.100°
C.110°
A
B
D.120°
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1下列图形中的角是圆周角的是(
A
B
C
D
解析:圆周角必须满足两个条件:·两个条件缺一不可.
(1)顶点在圆上;(2)两边都与圆相交
选项A,B不满足条件(2),选项D不满足条件(1),而选
项C同时满足条件(1)和条件(2).
1-1下列图形中的角是圆周角的是(B)
B
D
1-2[易错题]如图,AB所对的圆周角是∠ADB,∠ACB
CD所对的圆周角是
∠DAC,∠DBC,ABC所对的圆
周角是∠ADC,DAB所对的圆周角是∠BCD,弦
BD所对的圆周角是∠BCD,∠BAD
例2[内江中考]如图,点A,B,C,D在⊙O
B
上,∠AOC=120°,B是AC的中点,则∠D
的度数是(
A.30°
B.40°
C.50°
D.60°
>思路分析
已知条件
孤、弦、圆心
角之间的关系
圆周角定理
∠AOC=120°,
∠AOB=∠BOC=60→,
B是AC的中点
D=
40B-30
0
B
C
@思路分析
圆周角
直角三
圆周角
定理的
角形的
定理的
推论2
性质
推论1
∠ACB=90°
求∠BAC
∠BDC=∠BAC
解析:如图,连接AC
.AB是⊙O的直径,∴.∠ACB=90°.
.·∠ABC=38°,
.∠BAC=90°-∠ABC=52°.
∴.∠BDC=∠BAC=52°.
方法总结运用圆周角定理的推论2作辅助线的方法:
(1)有直径,通常作直径所对的圆周角,从而得到90°的角.简记
为:见直径作直角
(2)有90°的圆周角,通常作直径.简记为:有直角作直径
3-1用直角三角尺检查半圆形的工件,下列工件中合格
的是(C)
B.
3-2[柳州中考]如图,A,B,C,D是⊙0上的点,则图中与
∠A相等的角是(D)
A.∠B
B
A
B.∠C
E
0
C.∠DEB
D.∠D
3-4[黔东南州中考改编]如图,在Rt△ACB中,∠ACB=90°,
AC=6,BC=8,若以AC为直径的⊙O交AB于点D,则
CD的长为
4.8
A
D
0
C
B
D
A
B
C
>思路分析
四边形ABCD内接于⊙O
∠A+∠C=180°
∠A=105°
∠C=75
∠BOD=2∠C=150°
4-1[重庆中考A卷]如图,四边形ABCD内接于⊙O,若
∠A=80°,则C的度数是(B)
A.80°
B.100°
C.110°
A
B
D.120°
同课章节目录
