【同步作业】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.1 点和圆的位置关系 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.1 点和圆的位置关系 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览









文档简介
(共37张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1己知⊙O的直径为10cm,如果点P到圆心O的距
离是d,那么(
不要误当半径哦!
A.当d=8cm时,点P在⊙O内
B.当d=10cm时,点P在⊙O上
C.当d=5cm时,点P在⊙0上
D.当d=3cm时,点P在⊙O外
解析:.·⊙O的直径为10cm,.⊙O的半径r=5cm.
选项
比较d与r
点P的位置
结论
A
d=8 cm
d>r
⊙0外
×
B
d=10 cm
d>r
⊙0外
×
C
d=5 cm
d=r
⊙0上
V
D
d=3 cm
d⊙0内
×
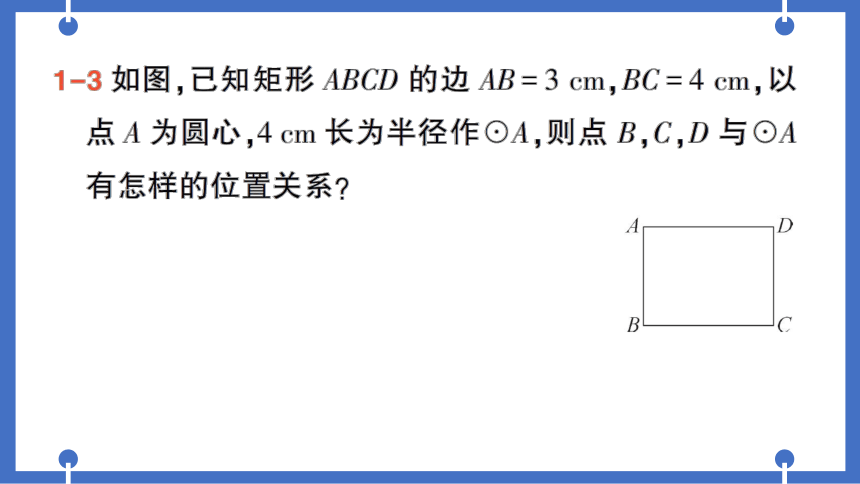
1-3如图,己知矩形ABCD的边AB=3cm,BC=4cm,以
点A为圆心,4cm长为半径作⊙A,则点B,C,D与⊙A
有怎样的位置关系?
解:如图,连接AC
·四边形ABCD是矩形,
.∴.∠B=90°,AD=BC=4cm.
B
:AB=3cm,.AC=√AB2+BC2=√32+42=5(cm).
.点B在⊙A内,点C在⊙A外,点D在⊙A上.
B
C
解:如图.连接AB,AC,分别作线段AB,AC的垂直平分
线,交点为O,则点O即为所求的经过A,B,C三点的圆
的圆心.
柳方法总结确定一个圆的圆心的方法:
(1)作出此圆任意两条弦(不平行)的垂直平分线,交点即为圆心
(2)利用直角三角尺作一条直径,中点即为圆心;或作两条直径,
交点即为圆心
2-1小明不慎把家中的圆形玻璃打碎了,其中四块碎片
如图所示,为得到与原来大小一样的圆形玻璃,小明
带到商店去的一块玻璃碎片应该是
②.(填序号)
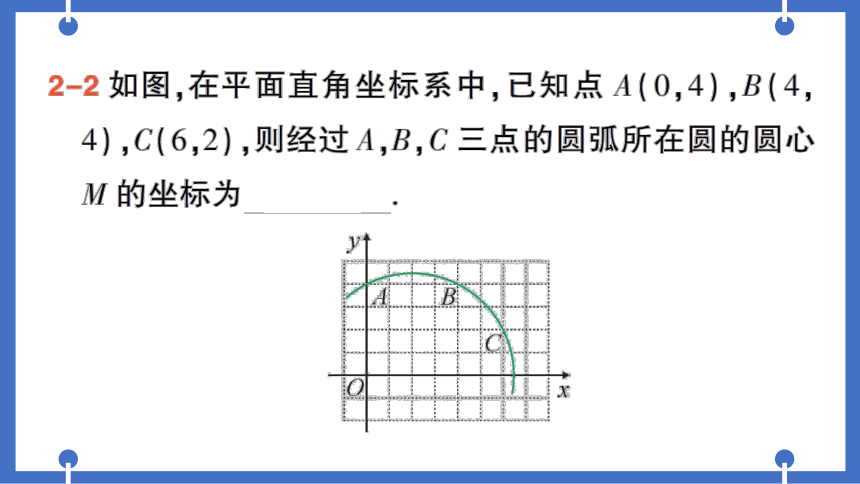
2-2如图,在平面直角坐标系中,己知点A(0,4),B(4,
4),C(6,2),则经过A,B,C三点的圆弧所在圆的圆心
M的坐标为(2,0)
2-3如图,点A,B,C在同一条直线上,点D在直线AB
外,过这4个点中的任意3点,能画的圆有3个
P
A
B
C
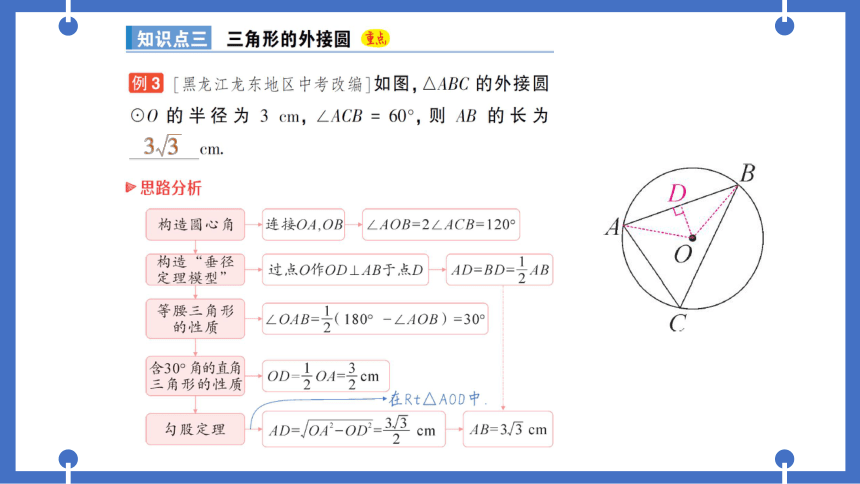
例3[黑龙江龙东地区中考改编]如图,△ABC的外接圆
⊙O的半径为3cm,∠ACB=60°,则AB的长为
cm.
B
D
A
C
思路分析
构造圆心角
连接OA,OB
∠AOB=2∠ACB=120°
构造“垂径
定理模型”
过点O作OD⊥AB于,点D
AD=BD-24B
等腰三角形
的性质
∠01B=2(180°-∠10B)=309
含30°角的直角
三角形的性质
0D-号0A=号cm
在Rt△AOD中
勾股定理
1D=0A2-0D=3
cm
4B=3/3 cm
2
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1己知⊙O的直径为10cm,如果点P到圆心O的距
离是d,那么(
不要误当半径哦!
A.当d=8cm时,点P在⊙O内
B.当d=10cm时,点P在⊙O上
C.当d=5cm时,点P在⊙0上
D.当d=3cm时,点P在⊙O外
解析:.·⊙O的直径为10cm,.⊙O的半径r=5cm.
选项
比较d与r
点P的位置
结论
A
d=8 cm
d>r
⊙0外
×
B
d=10 cm
d>r
⊙0外
×
C
d=5 cm
d=r
⊙0上
V
D
d=3 cm
d
×
1-3如图,己知矩形ABCD的边AB=3cm,BC=4cm,以
点A为圆心,4cm长为半径作⊙A,则点B,C,D与⊙A
有怎样的位置关系?
解:如图,连接AC
·四边形ABCD是矩形,
.∴.∠B=90°,AD=BC=4cm.
B
:AB=3cm,.AC=√AB2+BC2=√32+42=5(cm).
.点B在⊙A内,点C在⊙A外,点D在⊙A上.
B
C
解:如图.连接AB,AC,分别作线段AB,AC的垂直平分
线,交点为O,则点O即为所求的经过A,B,C三点的圆
的圆心.
柳方法总结确定一个圆的圆心的方法:
(1)作出此圆任意两条弦(不平行)的垂直平分线,交点即为圆心
(2)利用直角三角尺作一条直径,中点即为圆心;或作两条直径,
交点即为圆心
2-1小明不慎把家中的圆形玻璃打碎了,其中四块碎片
如图所示,为得到与原来大小一样的圆形玻璃,小明
带到商店去的一块玻璃碎片应该是
②.(填序号)
2-2如图,在平面直角坐标系中,己知点A(0,4),B(4,
4),C(6,2),则经过A,B,C三点的圆弧所在圆的圆心
M的坐标为(2,0)
2-3如图,点A,B,C在同一条直线上,点D在直线AB
外,过这4个点中的任意3点,能画的圆有3个
P
A
B
C
例3[黑龙江龙东地区中考改编]如图,△ABC的外接圆
⊙O的半径为3cm,∠ACB=60°,则AB的长为
cm.
B
D
A
C
思路分析
构造圆心角
连接OA,OB
∠AOB=2∠ACB=120°
构造“垂径
定理模型”
过点O作OD⊥AB于,点D
AD=BD-24B
等腰三角形
的性质
∠01B=2(180°-∠10B)=309
含30°角的直角
三角形的性质
0D-号0A=号cm
在Rt△AOD中
勾股定理
1D=0A2-0D=3
cm
4B=3/3 cm
2
同课章节目录
