【同步作业】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.2 直线和圆的位置关系 第3课时 切线长定理和三角形的内切圆 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.2 直线和圆的位置关系 第3课时 切线长定理和三角形的内切圆 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览






文档简介
(共34张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
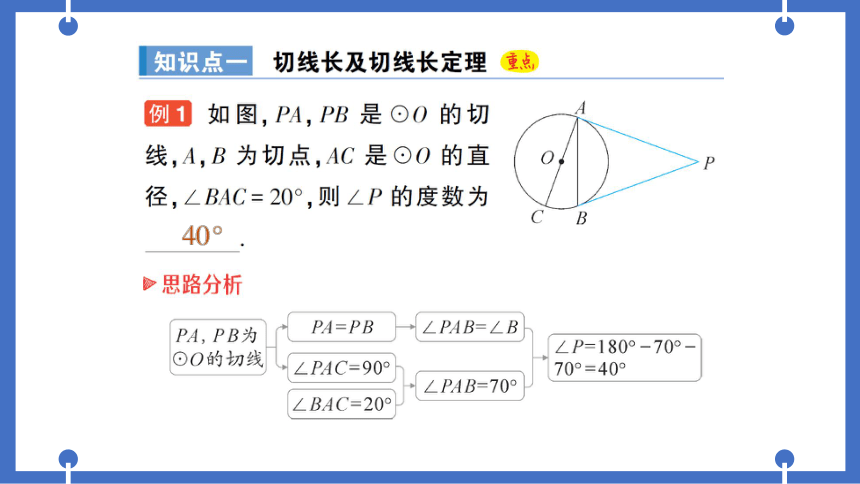
例1如图,PA,PB是⊙O的切
线,A,B为切点,AC是⊙O的直
径,∠BAC=20°,则∠P的度数为
C
B
②思路分析
PA,PB为
PA=PB
∠PAB=∠B
∠P=180°-70°-
⊙O的切线
∠PAC=90°
70°=40°
∠PAB=70°
∠BAC=20°
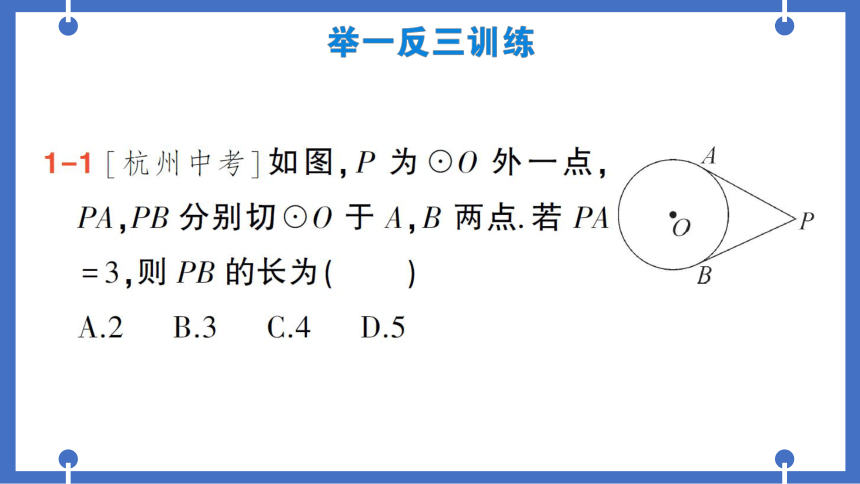
1-1[杭州中考]如图,P为⊙0外一点,
A
PA,PB分别切⊙O于A,B两点.若PA
=3,则PB的长为(B)
B
A.2
B.3
C.4
D.5
1-2[益阳中考]如图,PA,PB为⊙O的切线,
切点分别为A,B,PO交AB于点C,延长
P0交⊙O于点D.下列结论不一定成立的
是(D)
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB平分PD
1-3如图是用直尺、含60°角的三角尺和
光盘摆放而成的,A为三角尺的斜边与
00
直尺的交点,B为光盘与直尺的唯一
交点,C为三角尺与光盘的唯一交点.若AB=3,则光盘
的直径是
6/3
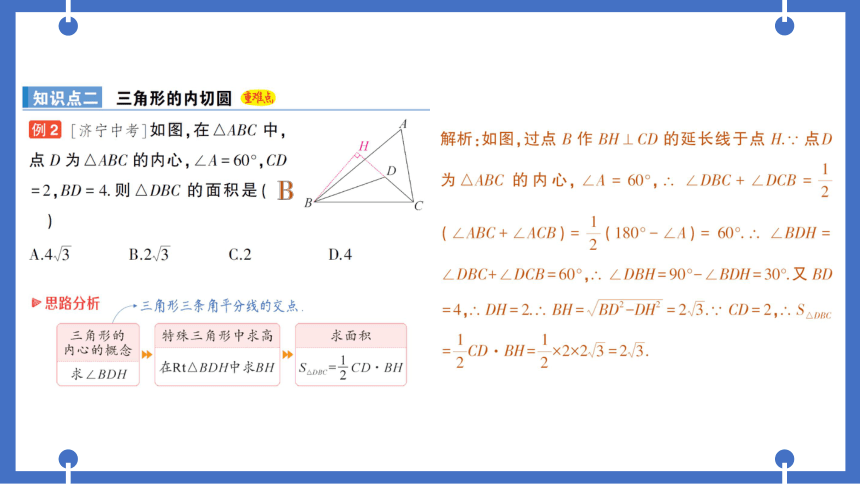
例2[济宁中考]如图,在△ABC中,
H
点D为△ABC的内心,∠A=60°,CD
=2,BD=4.则△DBC的面积是(
B
A.4/3
B.2/3
C.2
D.4
D思路分析
·三角形三条角平分线的交点,
三角形的
特殊三角形中求高
求面积
内心的概念
求∠BDH
在Rt△BDH中求BH
解析:如图,过点B作BH⊥CD的延长线于点H..·点D
为△ABC的内心,∠A=60°,.∠DBC+∠DCB=
2
(∠ABC+LACB)=2(180°-∠A)=60°.∠BDW=
∠DBC+∠DCB=60°,.∴.∠DBH=90°-∠BDH=30°.又BD
=4,.DH=2..BH=VBD2-D=2W3.CD=2,∴.S△Dsc
CD·BH=。×2×23=2W3.
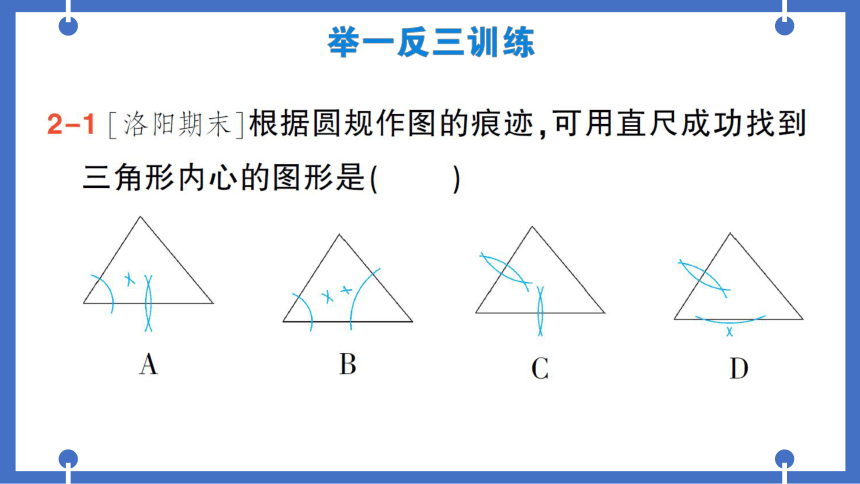
2-1「洛阳期末]根据圆规作图的痕迹,可用直尺成功找到
三角形内心的图形是(B)
A
B
G
D
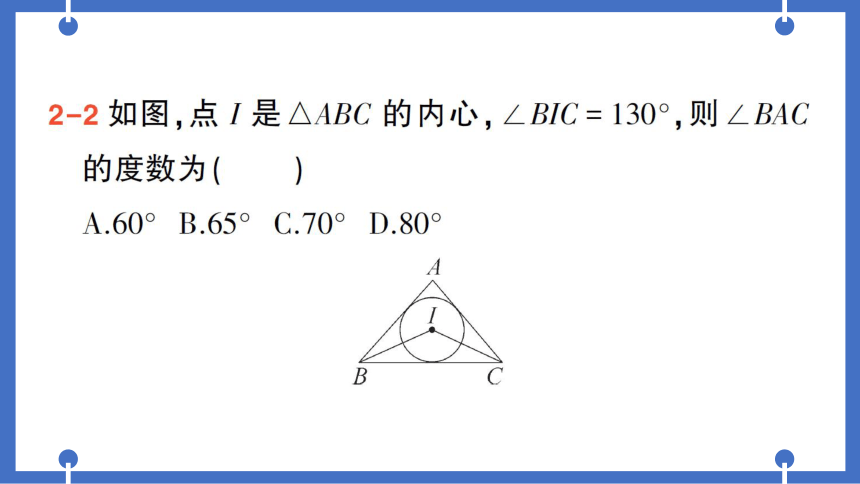
2-2如图,点I是△ABC的内心,∠BIC=130°,则∠BAC
的度数为(D)
A.60°B.65°C.70°D.80°
A
0
B
C
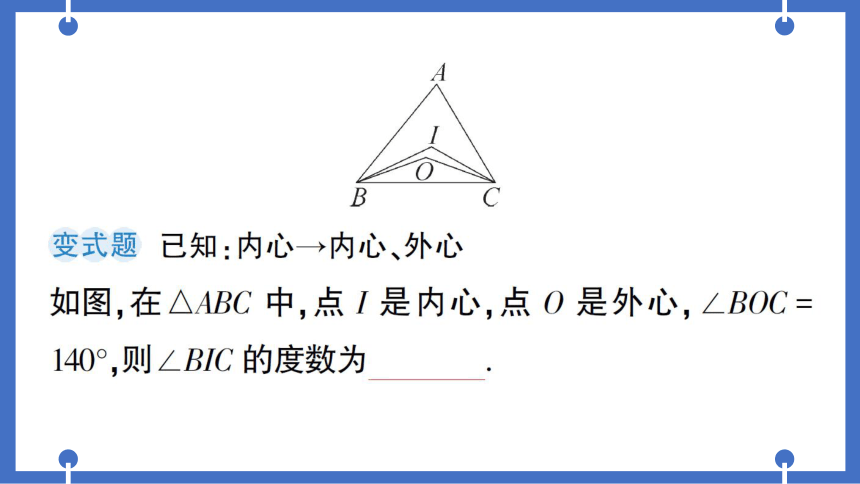
2-3如图,在△ABC中,点O是△ABC的内
心,连接OA,OB,OC.当AB=4,BC=5,AC
=6时,记△AOB,△BOC,△AOC的面积
B
分别为S1,S2,S3,则S1:S2:S3的值为4:5:6
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1如图,PA,PB是⊙O的切
线,A,B为切点,AC是⊙O的直
径,∠BAC=20°,则∠P的度数为
C
B
②思路分析
PA,PB为
PA=PB
∠PAB=∠B
∠P=180°-70°-
⊙O的切线
∠PAC=90°
70°=40°
∠PAB=70°
∠BAC=20°
1-1[杭州中考]如图,P为⊙0外一点,
A
PA,PB分别切⊙O于A,B两点.若PA
=3,则PB的长为(B)
B
A.2
B.3
C.4
D.5
1-2[益阳中考]如图,PA,PB为⊙O的切线,
切点分别为A,B,PO交AB于点C,延长
P0交⊙O于点D.下列结论不一定成立的
是(D)
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB平分PD
1-3如图是用直尺、含60°角的三角尺和
光盘摆放而成的,A为三角尺的斜边与
00
直尺的交点,B为光盘与直尺的唯一
交点,C为三角尺与光盘的唯一交点.若AB=3,则光盘
的直径是
6/3
例2[济宁中考]如图,在△ABC中,
H
点D为△ABC的内心,∠A=60°,CD
=2,BD=4.则△DBC的面积是(
B
A.4/3
B.2/3
C.2
D.4
D思路分析
·三角形三条角平分线的交点,
三角形的
特殊三角形中求高
求面积
内心的概念
求∠BDH
在Rt△BDH中求BH
解析:如图,过点B作BH⊥CD的延长线于点H..·点D
为△ABC的内心,∠A=60°,.∠DBC+∠DCB=
2
(∠ABC+LACB)=2(180°-∠A)=60°.∠BDW=
∠DBC+∠DCB=60°,.∴.∠DBH=90°-∠BDH=30°.又BD
=4,.DH=2..BH=VBD2-D=2W3.CD=2,∴.S△Dsc
CD·BH=。×2×23=2W3.
2-1「洛阳期末]根据圆规作图的痕迹,可用直尺成功找到
三角形内心的图形是(B)
A
B
G
D
2-2如图,点I是△ABC的内心,∠BIC=130°,则∠BAC
的度数为(D)
A.60°B.65°C.70°D.80°
A
0
B
C
2-3如图,在△ABC中,点O是△ABC的内
心,连接OA,OB,OC.当AB=4,BC=5,AC
=6时,记△AOB,△BOC,△AOC的面积
B
分别为S1,S2,S3,则S1:S2:S3的值为4:5:6
同课章节目录
