【同步作业】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.2 直线和圆的位置关系 专题十三 证明切线的两种常用方法 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 24.2 点和圆、直线和圆的位置关系 24.2.2 直线和圆的位置关系 专题十三 证明切线的两种常用方法 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览





文档简介
(共13张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
类型一
直线过圆上一点
例1
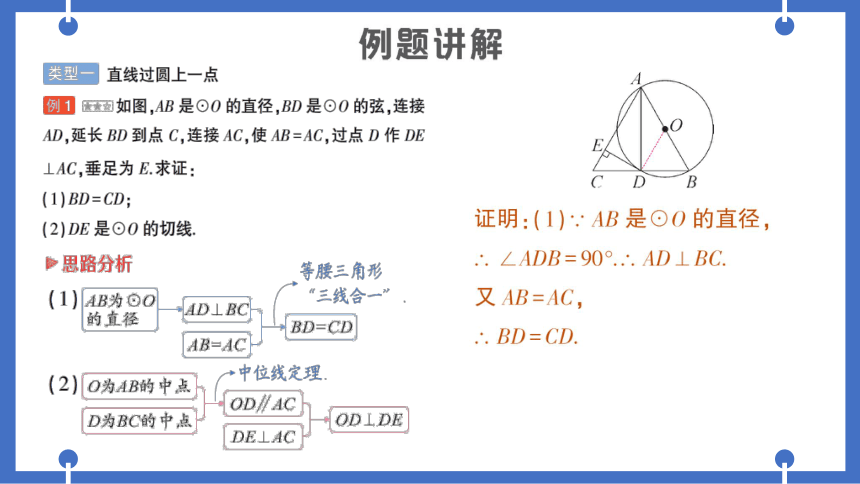
如图,AB是⊙O的直径,BD是⊙O的弦,连接
AD,延长BD到点C,连接AC,使AB=AC,过点D作DE
②思路分析
等腰三角形
(1)AB为⊙O
“三线合一
的直径
AD⊥BC
BD=CD
AB-AC
中位线定理
(2)O为AB的中点
OD∥AC
D为BC的中点
OD⊥DE
DE⊥AC
证明:(1)·AB是⊙0的直径
.∠ADB=90°..AD⊥BC.
又AB=AC,
.BD=CD.
(2)如图,连接OD
.·OA=OB,BD=CD,
.OD是△ABC的中位线.
.OD∥AC
另解:AB=AC
∴∠ABC=∠C.
义DE⊥AC,.OD⊥DE.
0B=0D,
.·OD为⊙0的半径,
·∠ABC=ODB,
∴∠0DB=∠C
.DE是⊙O的切线
·OD∥AC
一、借助角度转化90
1-1如图,在Rt△ABC中,∠BCA=90°,以BC为直
径的⊙O交AB于点P,Q是AC的中点.求证:PQ是
⊙O的切线.
B
P
0,
A
C
2
证明:如图,连接OP,CP..·BC为⊙O的直径,
.∴.∠BPC=∠APC=90°.
Q是AC的中点,
∴.PQ=CQ=AQ.∠CPQ=∠PCQ
.·OP=OC,.∴.∠OPC=∠OCP.
∴.∠OPQ=∠OCQ=90°.∴.PQ⊥OP.
又OP是⊙O的半径,∴.PQ是⊙O的切线.
B
P
A
C
9
二、利用全等转化90
1-2★[遵义期末1如图,PA是⊙O的切线,A为切点,连
接PO交⊙O于点C,PC=OC,⊙0上有一点B,且∠POB
=60°,连接PB.
(1)探究OC和AC的数量关系,并说明理由;
(2)求证:PB是⊙O的切线
B.
0
C
P
A
(2)
证Rt△ABD≌
AB-AF
Rt△AFD
求AC
证Rt△BDE≌
BE=FC
Rt△FDC
(1)证明:如图,过点D作DF⊥AC于点F..·∠ABC=90°,
..AB⊥B
又AD平分∠BAC,DF⊥AC,
.DF=DB,即DF是⊙D的半径
.AC是⊙D的切线
A
D
0
M
B
C
证明:如图,过点O作ON⊥BC于点N.
A
·四边形ABCD是正方形,
M
AC是对角线,
..CA平分∠BCD.
B
.·CD与⊙O相切于点M,.CD⊥OM.
.ON=OM..ON为⊙O的半径.
又BC⊥ON,.BC为⊙O的切线.
易储点:证明一条直线是圆的切线时,如果没有明确直线与圆是否有公
共点,应“作垂直,证半径”,而很多同学易储解为“连半径,证垂直”.
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
类型一
直线过圆上一点
例1
如图,AB是⊙O的直径,BD是⊙O的弦,连接
AD,延长BD到点C,连接AC,使AB=AC,过点D作DE
②思路分析
等腰三角形
(1)AB为⊙O
“三线合一
的直径
AD⊥BC
BD=CD
AB-AC
中位线定理
(2)O为AB的中点
OD∥AC
D为BC的中点
OD⊥DE
DE⊥AC
证明:(1)·AB是⊙0的直径
.∠ADB=90°..AD⊥BC.
又AB=AC,
.BD=CD.
(2)如图,连接OD
.·OA=OB,BD=CD,
.OD是△ABC的中位线.
.OD∥AC
另解:AB=AC
∴∠ABC=∠C.
义DE⊥AC,.OD⊥DE.
0B=0D,
.·OD为⊙0的半径,
·∠ABC=ODB,
∴∠0DB=∠C
.DE是⊙O的切线
·OD∥AC
一、借助角度转化90
1-1如图,在Rt△ABC中,∠BCA=90°,以BC为直
径的⊙O交AB于点P,Q是AC的中点.求证:PQ是
⊙O的切线.
B
P
0,
A
C
2
证明:如图,连接OP,CP..·BC为⊙O的直径,
.∴.∠BPC=∠APC=90°.
Q是AC的中点,
∴.PQ=CQ=AQ.∠CPQ=∠PCQ
.·OP=OC,.∴.∠OPC=∠OCP.
∴.∠OPQ=∠OCQ=90°.∴.PQ⊥OP.
又OP是⊙O的半径,∴.PQ是⊙O的切线.
B
P
A
C
9
二、利用全等转化90
1-2★[遵义期末1如图,PA是⊙O的切线,A为切点,连
接PO交⊙O于点C,PC=OC,⊙0上有一点B,且∠POB
=60°,连接PB.
(1)探究OC和AC的数量关系,并说明理由;
(2)求证:PB是⊙O的切线
B.
0
C
P
A
(2)
证Rt△ABD≌
AB-AF
Rt△AFD
求AC
证Rt△BDE≌
BE=FC
Rt△FDC
(1)证明:如图,过点D作DF⊥AC于点F..·∠ABC=90°,
..AB⊥B
又AD平分∠BAC,DF⊥AC,
.DF=DB,即DF是⊙D的半径
.AC是⊙D的切线
A
D
0
M
B
C
证明:如图,过点O作ON⊥BC于点N.
A
·四边形ABCD是正方形,
M
AC是对角线,
..CA平分∠BCD.
B
.·CD与⊙O相切于点M,.CD⊥OM.
.ON=OM..ON为⊙O的半径.
又BC⊥ON,.BC为⊙O的切线.
易储点:证明一条直线是圆的切线时,如果没有明确直线与圆是否有公
共点,应“作垂直,证半径”,而很多同学易储解为“连半径,证垂直”.
同课章节目录
