【同步作业】人教版九(上) 24.4 弧长和扇形面积 第1课时 弧长和扇形面积 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 24.4 弧长和扇形面积 第1课时 弧长和扇形面积 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览







文档简介
(共31张PPT)
●
点易错·训练课
秒本章知识梳理
歌点状元·提分课
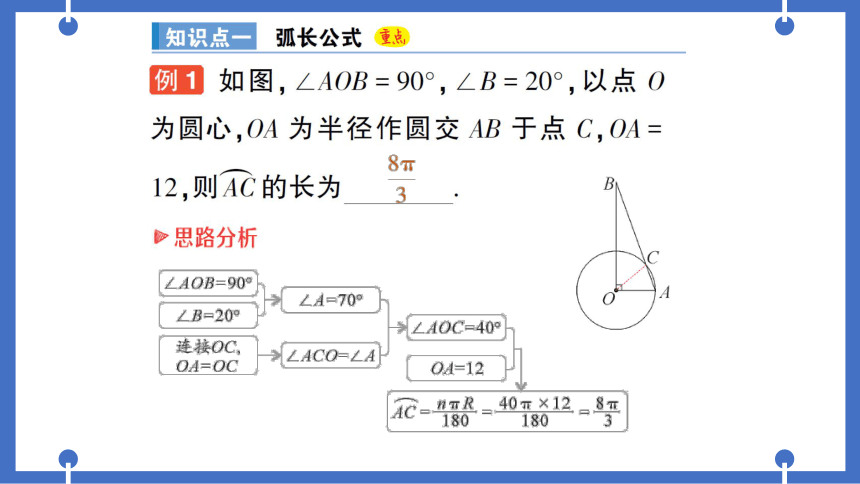
例1如图,∠AOB=90°,∠B=20°,以点0
为圆心,OA为半径作圆交AB于点C,OA=
12,则AC的长为
1-1「温州中考1若扇形的圆心角为90°,半径为6,则该扇
形的弧长为(C)
B.2π
2
D.6π
变式题求弧长→求半径
75的圆心角所对的弧长是2.5πcm,则此弧所在圆的
半径是
cm.
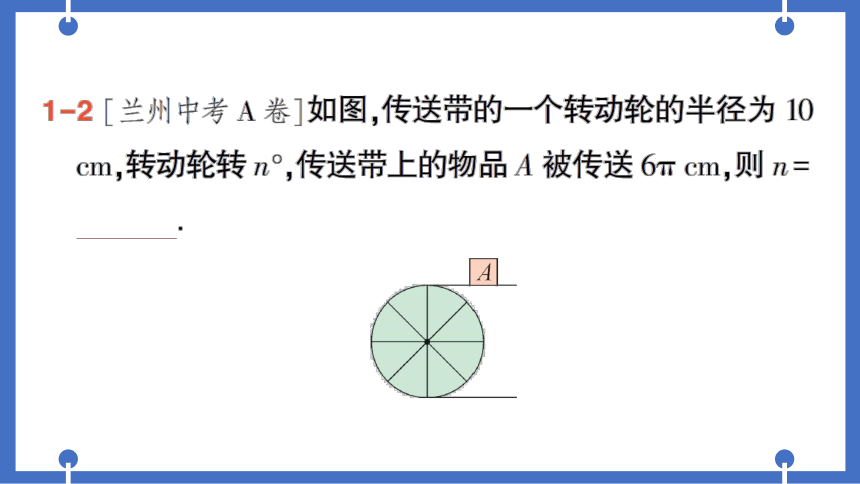
1-2[兰州中考A卷]如图,传送带的一个转动轮的半径为10
cm,转动轮转n°,传送带上的物品A被传送6πcm,则n=
108
A
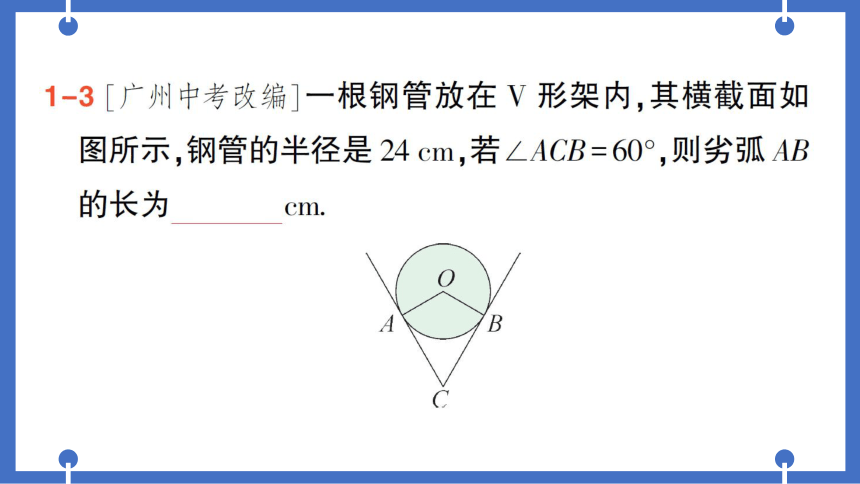
1-3[广州中考改编]一根钢管放在V形架内,其横截面如
图所示,钢管的半径是24cm,若∠ACB=60°,则劣弧AB
的长为16π
cm.
B
例2[转化思想]如图,在⊙0中,OA=2,∠AOB=90°,则
图中阴影部分的面积为(
A
2
B.T-√/2
2
C
2
D.π-2
A
B
2
90T×22
解析:∠AOB=90°,.S扇形0AB
360
=T,S△A0B=)>
2
2X2=2..S阴影=S扇形01B-S△A0B=T-2.
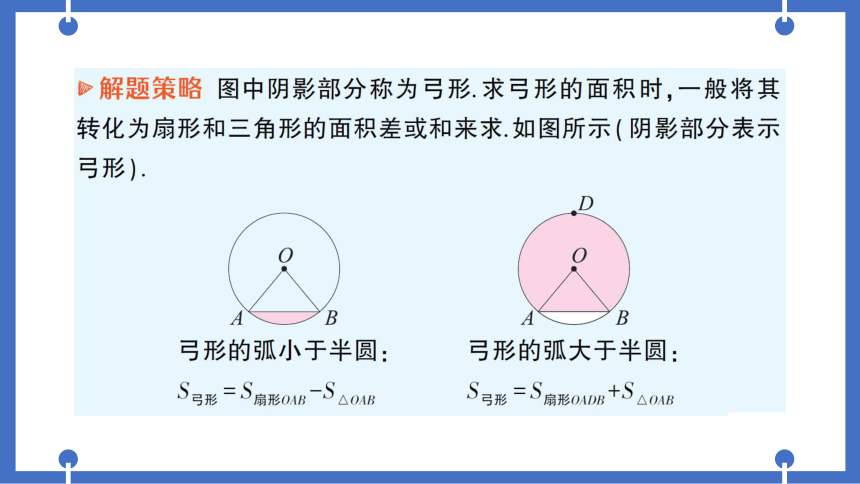
>解题策略图中阴影部分称为弓形.求弓形的面积时,一般将其
转化为扇形和三角形的面积差或和来求.如图所示(阴影部分表示
弓形).
D
A
B
B
弓形的弧小于半圆:
弓形的弧大于半圆:
S号形=S扇形OAB-S△01B
S号形=S扇形OADB+S△OAB
2-1「长沙中考改编]一个扇形的半径为6,圆心角为120°,则
该扇形的面积是
12T
2-2面积为240m,半径为24的扇形的圆心角为
150°
2-3[古代数学文化]《九章算术》是中国古代最重要的一
部数学专著,第一章“方田”中己讲述了平面几何图形
面积的计算方法,比如扇形的计算,“今有宛田,下周
三十步,径十六步,问为田几何?”大致意思为:现有一
块扇形的田,弧长30步,其所在圆的直径是16步,则这
块田的面积为
12
)平方步.
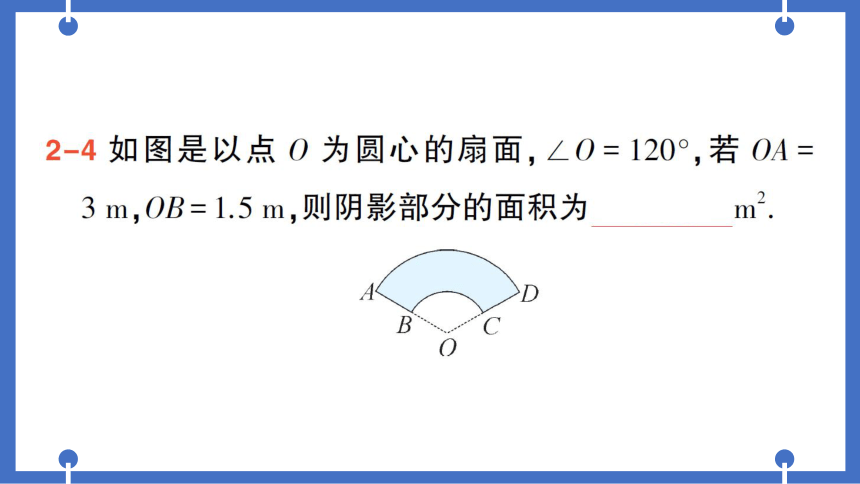
2-4如图是以点0为圆心的扇面,∠0=120°,若0A=
3m,OB=1.5m,则阴影部分的面积为
2.25πm2.
2-5[金昌中考]若一个扇形的圆心角为60°,面积为
cm,则这个扇形的弧长为
cm.(结果保留π)
3
题型一
应用弧长公式解决运动路线问题
例3
女☆如图,在Rt△ABC中,∠B
=90°,∠A=30°,BC=2,将△ABC绕
点C顺时针旋转得到△A'B'C,点A,
B'
C,B'在同一条直线上,则点A经过的路线的长度是
●
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1如图,∠AOB=90°,∠B=20°,以点0
为圆心,OA为半径作圆交AB于点C,OA=
12,则AC的长为
1-1「温州中考1若扇形的圆心角为90°,半径为6,则该扇
形的弧长为(C)
B.2π
2
D.6π
变式题求弧长→求半径
75的圆心角所对的弧长是2.5πcm,则此弧所在圆的
半径是
cm.
1-2[兰州中考A卷]如图,传送带的一个转动轮的半径为10
cm,转动轮转n°,传送带上的物品A被传送6πcm,则n=
108
A
1-3[广州中考改编]一根钢管放在V形架内,其横截面如
图所示,钢管的半径是24cm,若∠ACB=60°,则劣弧AB
的长为16π
cm.
B
例2[转化思想]如图,在⊙0中,OA=2,∠AOB=90°,则
图中阴影部分的面积为(
A
2
B.T-√/2
2
C
2
D.π-2
A
B
2
90T×22
解析:∠AOB=90°,.S扇形0AB
360
=T,S△A0B=)>
2
2X2=2..S阴影=S扇形01B-S△A0B=T-2.
>解题策略图中阴影部分称为弓形.求弓形的面积时,一般将其
转化为扇形和三角形的面积差或和来求.如图所示(阴影部分表示
弓形).
D
A
B
B
弓形的弧小于半圆:
弓形的弧大于半圆:
S号形=S扇形OAB-S△01B
S号形=S扇形OADB+S△OAB
2-1「长沙中考改编]一个扇形的半径为6,圆心角为120°,则
该扇形的面积是
12T
2-2面积为240m,半径为24的扇形的圆心角为
150°
2-3[古代数学文化]《九章算术》是中国古代最重要的一
部数学专著,第一章“方田”中己讲述了平面几何图形
面积的计算方法,比如扇形的计算,“今有宛田,下周
三十步,径十六步,问为田几何?”大致意思为:现有一
块扇形的田,弧长30步,其所在圆的直径是16步,则这
块田的面积为
12
)平方步.
2-4如图是以点0为圆心的扇面,∠0=120°,若0A=
3m,OB=1.5m,则阴影部分的面积为
2.25πm2.
2-5[金昌中考]若一个扇形的圆心角为60°,面积为
cm,则这个扇形的弧长为
cm.(结果保留π)
3
题型一
应用弧长公式解决运动路线问题
例3
女☆如图,在Rt△ABC中,∠B
=90°,∠A=30°,BC=2,将△ABC绕
点C顺时针旋转得到△A'B'C,点A,
B'
C,B'在同一条直线上,则点A经过的路线的长度是
同课章节目录
