【同步作业】人教版九(上) 24.4 弧长和扇形面积 专题十七 求阴影部分的面积 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 24.4 弧长和扇形面积 专题十七 求阴影部分的面积 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览







文档简介
(共22张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1
如图,在口ABCD中,∠B=60°,⊙C的半径为
3,则图中阴影部分的面积是(
A.T
A
B.2π
B
C.3π
D.6π
D思路分析
□ABCD
AB∥CD
∠B+∠C=180°
S影=
nTR2
∠C=120°
360
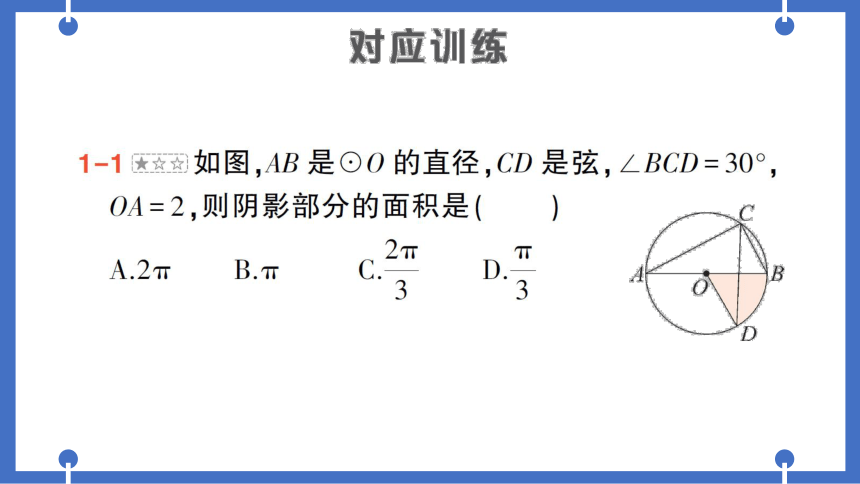
1-1如图,AB是⊙O的直径,CD是弦,∠BCD=30°,
OA=2,则阴影部分的面积是(C)
A.2π
B.π
D
3
3
C
A
B
D
1-2:☆「贺州中考改编]如图,在边长为2的等边三角形
ABC中,D是边BC的中点,以点A为圆心,AD长为半
径作弧,分别交AB,AC于E,F两点,则图中阴影部分
的面积为
2
A
E
F
B
D
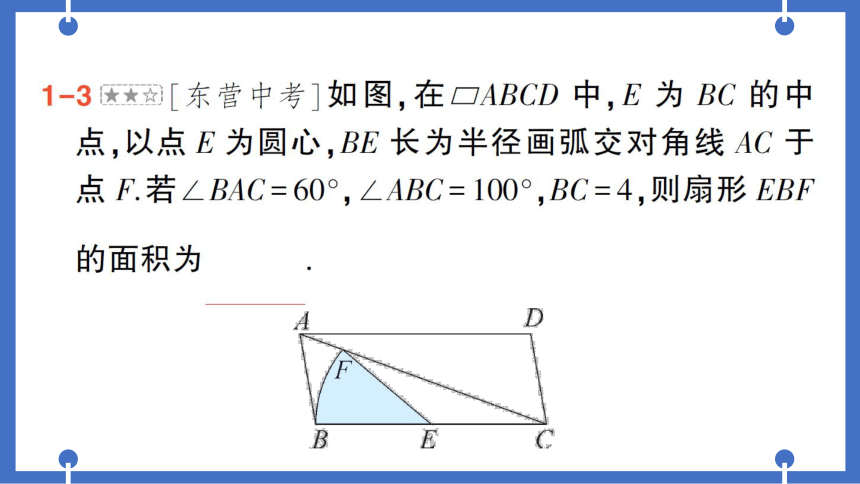
1-3「东营中考]如图,在口ABCD中,E为BC的中
点,以点E为圆心,BE长为半径画弧交对角线AC于
点F.若∠BAC=60°,∠ABC=100°,BC=4,则扇形EBF
4不
的面积为
1-4质[凉山州中考改编]家具厂利用如图所示的直径为
1m的圆形材料加工成一种扇形家具部件,已知扇形
的圆心角∠BAC=90°,则扇形部件的面积为
m.
8
例2
★肉[吉林中考]如图,在Rt△ABC中,∠C
=90°,∠A=30°,BC=2.以点C为圆心,CB长为
半径画弧,分别交AC,AB于点D,E,则图中阴影
部分的面积为
结果保留π).
>思路分析
构造特殊
面积和差
求面积
三角形
S阴影=S肩形CcaE
等边三角形
S
SABCE
形CBE)
BCE
SABCE
解析:如图,连接CE..·∠ACB=90°,∠A=30°,∴.∠CBA=
90°-∠A=60°.
CE=CB,.△BCE为等边三角形,
∴.∠ECB=60°,BE=BC=CE=2,
60π×2
2
扇形CBE
π.过点E作EF⊥BC于点F,则
360
BF=
BC=1,∴.EF=VBE-BF=V22-1=3,.SAE
2
2
X2X3=3,'.S阴影=S扇形C5-S△0E
2
3/3.
B
E
O
D
2-
2★西「整体思想[包头中考]如图,在Rt△ABC中,
∠ACB=90°,AB=√5,BC=2,以点A为圆心,AC的长为半
径画弧,交AB于点D,以点B为圆心,AC的长为半径画
弧,交AB于点E,交BC于点F,则图中阴影部分的面积
为(D)
T
A.8-π
B.4-m
C.2-
D.1
4
4
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
例1
如图,在口ABCD中,∠B=60°,⊙C的半径为
3,则图中阴影部分的面积是(
A.T
A
B.2π
B
C.3π
D.6π
D思路分析
□ABCD
AB∥CD
∠B+∠C=180°
S影=
nTR2
∠C=120°
360
1-1如图,AB是⊙O的直径,CD是弦,∠BCD=30°,
OA=2,则阴影部分的面积是(C)
A.2π
B.π
D
3
3
C
A
B
D
1-2:☆「贺州中考改编]如图,在边长为2的等边三角形
ABC中,D是边BC的中点,以点A为圆心,AD长为半
径作弧,分别交AB,AC于E,F两点,则图中阴影部分
的面积为
2
A
E
F
B
D
1-3「东营中考]如图,在口ABCD中,E为BC的中
点,以点E为圆心,BE长为半径画弧交对角线AC于
点F.若∠BAC=60°,∠ABC=100°,BC=4,则扇形EBF
4不
的面积为
1-4质[凉山州中考改编]家具厂利用如图所示的直径为
1m的圆形材料加工成一种扇形家具部件,已知扇形
的圆心角∠BAC=90°,则扇形部件的面积为
m.
8
例2
★肉[吉林中考]如图,在Rt△ABC中,∠C
=90°,∠A=30°,BC=2.以点C为圆心,CB长为
半径画弧,分别交AC,AB于点D,E,则图中阴影
部分的面积为
结果保留π).
>思路分析
构造特殊
面积和差
求面积
三角形
S阴影=S肩形CcaE
等边三角形
S
SABCE
形CBE)
BCE
SABCE
解析:如图,连接CE..·∠ACB=90°,∠A=30°,∴.∠CBA=
90°-∠A=60°.
CE=CB,.△BCE为等边三角形,
∴.∠ECB=60°,BE=BC=CE=2,
60π×2
2
扇形CBE
π.过点E作EF⊥BC于点F,则
360
BF=
BC=1,∴.EF=VBE-BF=V22-1=3,.SAE
2
2
X2X3=3,'.S阴影=S扇形C5-S△0E
2
3/3.
B
E
O
D
2-
2★西「整体思想[包头中考]如图,在Rt△ABC中,
∠ACB=90°,AB=√5,BC=2,以点A为圆心,AC的长为半
径画弧,交AB于点D,以点B为圆心,AC的长为半径画
弧,交AB于点E,交BC于点F,则图中阴影部分的面积
为(D)
T
A.8-π
B.4-m
C.2-
D.1
4
4
同课章节目录
