【同步作业】人教版九(上) 第21章 一元二次方程 专题二 围矩形问题——教材P25复习题21T8的变式及应用 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 第21章 一元二次方程 专题二 围矩形问题——教材P25复习题21T8的变式及应用 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览





文档简介
(共12张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
解:设垂直于墙的一边长为xm,则平行于墙的一边长为
(20-2.x)m.
由题意得x(20-2x)=50.
解得x1=x2=5.所以20-2x=10.
答:矩形场地的长和宽分别为10m,5m.
变式一一个矩形,墙长有限制
1.如图,在足够大的空地上有一段长为20m的旧
墙MN,某人利用I旧墙和木栏围成一个矩形菜园AB
CD,其中AD≤MW,己知矩形菜园的一边靠墙,另三边
一共用了100m木栏,所围成的矩形菜园的面积为
W
222254222
A
D
B
C
解:设BC的长为xm(0100-x
长为
m.
2
依题意,得七·
100-x
=450.
2
整理,得x2-100x+900=0.
解得x1=10,x2=90(不合题意,舍去).
答:BC的长为10m.
变式二
两个矩形,墙长有限制
2.如图,有长为30m的篱笆,一面利用墙(墙的最大
可用长度为10m),围成中间隔有一道篱笆(平行于
AB)的矩形花圃
(1)设花圃的一边AB为xm,则BC的长可用含x的代数
式表示为(30-3x)
m.
(2)当AB的长是多少米时,围成的花圃面积为63m2
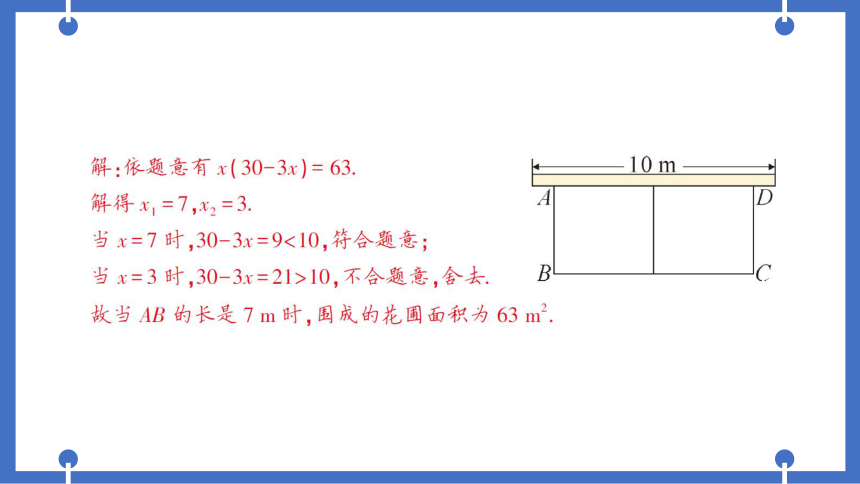
解:依题意有x(30-3x)=63.
10m
解得心1=7,x2=3.
A
当x=7时,30-3x=9<10,符合题意;
当x=3时,30-3x=21>10,不合题意,会去.
B
C
故当AB的长是7m时,围成的花圃面积为63m2.
变式三一个矩形,墙长有限制,中间有一个门
3.安某村准备在该村山脚下围一块面积为600m2的
矩形试验茶园,便于成功后大面积推广.如图,茶园一
面靠墙,墙长35m,另外三面用69m长的篱笆围成,其
中一边开有一扇1m宽的门(不用篱笆).求这个茶园
的长和宽
A
D
门
B
C
解:设AB的长为xm,
A
则BC的长为69+1-2x=(70-2x)m.
根据题意,得x(70-2x)=600.
整理,得2-35x+300=0.解得x1=15,x2=20
B
当x=15时,70-2x=40>35,不合题意,舍去;
当x=20时,70-2x=30<35,符合题意.
答:这个茶园的长和宽分别为30m,20m.
变式四
两个矩形,墙长有限制,中间有多个门
4.★某农场要建一个饲养场(矩形ABCD),饲养场的
一面靠墙(墙的最大可用长度为27m),另三边用木栏
围成,中间用木栏隔开,分成两个场地,并在如图所示
的三处各留1宽的门(不用木栏),建成后木栏总长
为57m,设CD的长为am.
(1)BC的长为
(60-3a)m(用含a的代数式表
示).
(2)若饲养场的面积为288m,求a的值,
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
解:设垂直于墙的一边长为xm,则平行于墙的一边长为
(20-2.x)m.
由题意得x(20-2x)=50.
解得x1=x2=5.所以20-2x=10.
答:矩形场地的长和宽分别为10m,5m.
变式一一个矩形,墙长有限制
1.如图,在足够大的空地上有一段长为20m的旧
墙MN,某人利用I旧墙和木栏围成一个矩形菜园AB
CD,其中AD≤MW,己知矩形菜园的一边靠墙,另三边
一共用了100m木栏,所围成的矩形菜园的面积为
W
222254222
A
D
B
C
解:设BC的长为xm(0
长为
m.
2
依题意,得七·
100-x
=450.
2
整理,得x2-100x+900=0.
解得x1=10,x2=90(不合题意,舍去).
答:BC的长为10m.
变式二
两个矩形,墙长有限制
2.如图,有长为30m的篱笆,一面利用墙(墙的最大
可用长度为10m),围成中间隔有一道篱笆(平行于
AB)的矩形花圃
(1)设花圃的一边AB为xm,则BC的长可用含x的代数
式表示为(30-3x)
m.
(2)当AB的长是多少米时,围成的花圃面积为63m2
解:依题意有x(30-3x)=63.
10m
解得心1=7,x2=3.
A
当x=7时,30-3x=9<10,符合题意;
当x=3时,30-3x=21>10,不合题意,会去.
B
C
故当AB的长是7m时,围成的花圃面积为63m2.
变式三一个矩形,墙长有限制,中间有一个门
3.安某村准备在该村山脚下围一块面积为600m2的
矩形试验茶园,便于成功后大面积推广.如图,茶园一
面靠墙,墙长35m,另外三面用69m长的篱笆围成,其
中一边开有一扇1m宽的门(不用篱笆).求这个茶园
的长和宽
A
D
门
B
C
解:设AB的长为xm,
A
则BC的长为69+1-2x=(70-2x)m.
根据题意,得x(70-2x)=600.
整理,得2-35x+300=0.解得x1=15,x2=20
B
当x=15时,70-2x=40>35,不合题意,舍去;
当x=20时,70-2x=30<35,符合题意.
答:这个茶园的长和宽分别为30m,20m.
变式四
两个矩形,墙长有限制,中间有多个门
4.★某农场要建一个饲养场(矩形ABCD),饲养场的
一面靠墙(墙的最大可用长度为27m),另三边用木栏
围成,中间用木栏隔开,分成两个场地,并在如图所示
的三处各留1宽的门(不用木栏),建成后木栏总长
为57m,设CD的长为am.
(1)BC的长为
(60-3a)m(用含a的代数式表
示).
(2)若饲养场的面积为288m,求a的值,
同课章节目录
