【同步作业】人教版九(上) 第21章 一元二次方程 本章归纳复习 (课件版)
文档属性
| 名称 | 【同步作业】人教版九(上) 第21章 一元二次方程 本章归纳复习 (课件版) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-30 16:35:23 | ||
图片预览










文档简介
(共43张PPT)
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
等号两边都是整式,只含有
个未知数(一元),
并且未知数的最高次数是
2
2
(二次)的方程
基
解(根):使方程左右两边
概念
相等的未知数的值
见根代入
→注意a,b,c的符号.
ax2+b.x+c=0(a≠0)
一般形式
一元二次
方程
解二次项系数是,一次项系数为
偶数的一元二次方程特别合适
直接开平方法:
解形如x2=p(p≥0)或(mx+n)2=
P(m≠0,p≥0)的方程
配方法:
配方这一步,方程两边同时加
上一次项系数④一半的平方
公式法:
-b±J62-4ac
代入求根公式⑤x
解
2a
(b2-4ac≥0))
因式分解法
把方程变形为a·b=0的形式,
则a=0,或b=0
只有当≠0,△≥0时,
才能用求根公式
方程有两个相等的实数
根→b2-4ac⑥
方程有两个不等的实数
根的判别式
根=→b2-4ac⑦>0
△=b2-4ac
方程无实数根二
b2-4ac⑧)<0
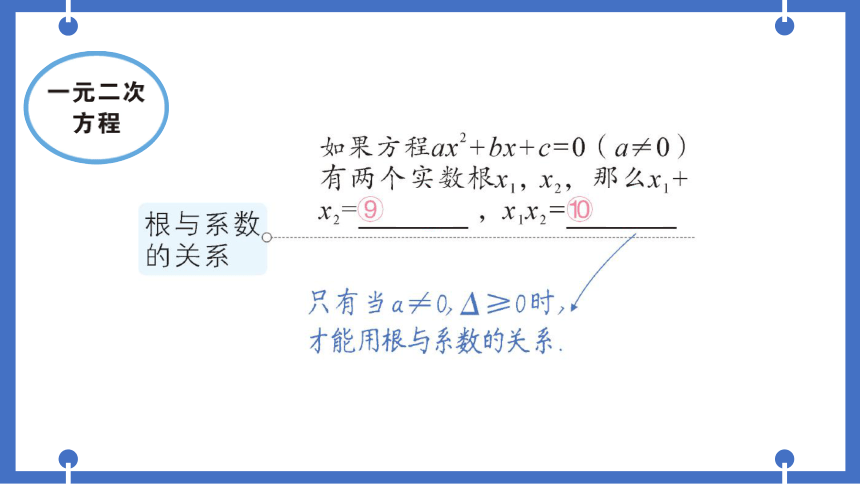
如果方程ax2+bx+c=0(a≠0)
有两个实数根x1,x2,那么x,+
根与系数
x2-⑨
a
1X2=10
a
的关系
只有当a≠0,△≥0时,4
才能用根与系数的关系、
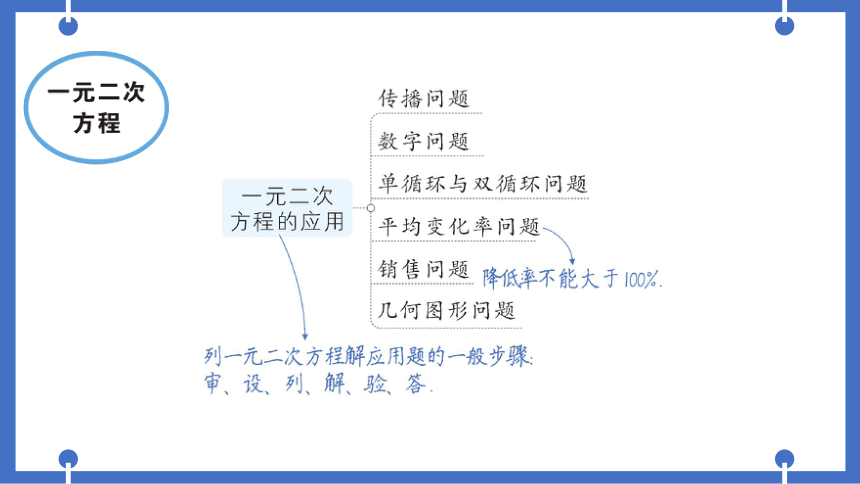
传播问题
数字问题
单循环与双循环问题
一元二次
方程的应用
平均变化率问题
销售问题
降低率不能大于100%
几何图形问题
列一元二次方程解应用题的一般步骤
审、设、列、解、验、答
高频考点
一元二次方程的有关概念
例1
☆「荆门中考]已知2是关于x的一元二次方程
kx2+(k2-2)x+2k+4=0的一个根,则k的值为
多思路分析
=2代入
一元二
k=0,
次方程
>k2+3k=0>
k,=-3
>k=-3
易忽略
k≠0
高频考点二一元二次方程的解法4
例2
改解下列方程:
(1)x2+6x=-7;
(2)2x2-3x-5=0;
(3)x2+4x=5(x+4).
解:(1)配方,得x2+6x+32=-7+32,(x+3)2=2.由此可得
x+3=±/2,X1=-3+√2,x2=-3-2.
(2)a=2,b=-3,c=-5.
4=b2-4ac=(-3)2-4×2×(-5)=49>0.
方程有两个不等的实数根
-b±√/b2-4ac3±7
3,即x,=
5
比三
2a
2,2=-1.
2-2★[新定义][恩施州恩施市期末改编]对于实数p,9,
我们用符号mn{p,q}表示p,q两数中较小的数,如
mn{1,2}=1,in{-√2,-V3}=-√3.若mn{(x-1)2,
x2}=1,则的值为2或-1·
●
点题型·提升课
馆点易错·
诊断课
点易错·训练课
秒本章知识梳理
歌点状元·提分课
等号两边都是整式,只含有
个未知数(一元),
并且未知数的最高次数是
2
2
(二次)的方程
基
解(根):使方程左右两边
概念
相等的未知数的值
见根代入
→注意a,b,c的符号.
ax2+b.x+c=0(a≠0)
一般形式
一元二次
方程
解二次项系数是,一次项系数为
偶数的一元二次方程特别合适
直接开平方法:
解形如x2=p(p≥0)或(mx+n)2=
P(m≠0,p≥0)的方程
配方法:
配方这一步,方程两边同时加
上一次项系数④一半的平方
公式法:
-b±J62-4ac
代入求根公式⑤x
解
2a
(b2-4ac≥0))
因式分解法
把方程变形为a·b=0的形式,
则a=0,或b=0
只有当≠0,△≥0时,
才能用求根公式
方程有两个相等的实数
根→b2-4ac⑥
方程有两个不等的实数
根的判别式
根=→b2-4ac⑦>0
△=b2-4ac
方程无实数根二
b2-4ac⑧)<0
如果方程ax2+bx+c=0(a≠0)
有两个实数根x1,x2,那么x,+
根与系数
x2-⑨
a
1X2=10
a
的关系
只有当a≠0,△≥0时,4
才能用根与系数的关系、
传播问题
数字问题
单循环与双循环问题
一元二次
方程的应用
平均变化率问题
销售问题
降低率不能大于100%
几何图形问题
列一元二次方程解应用题的一般步骤
审、设、列、解、验、答
高频考点
一元二次方程的有关概念
例1
☆「荆门中考]已知2是关于x的一元二次方程
kx2+(k2-2)x+2k+4=0的一个根,则k的值为
多思路分析
=2代入
一元二
k=0,
次方程
>k2+3k=0>
k,=-3
>k=-3
易忽略
k≠0
高频考点二一元二次方程的解法4
例2
改解下列方程:
(1)x2+6x=-7;
(2)2x2-3x-5=0;
(3)x2+4x=5(x+4).
解:(1)配方,得x2+6x+32=-7+32,(x+3)2=2.由此可得
x+3=±/2,X1=-3+√2,x2=-3-2.
(2)a=2,b=-3,c=-5.
4=b2-4ac=(-3)2-4×2×(-5)=49>0.
方程有两个不等的实数根
-b±√/b2-4ac3±7
3,即x,=
5
比三
2a
2,2=-1.
2-2★[新定义][恩施州恩施市期末改编]对于实数p,9,
我们用符号mn{p,q}表示p,q两数中较小的数,如
mn{1,2}=1,in{-√2,-V3}=-√3.若mn{(x-1)2,
x2}=1,则的值为2或-1·
同课章节目录
